Back to: Main Page > Mathématiques > Aspects de l'entropie en mathématiques
La théorie de l'information : l'origine de l'entropie
La théorie de l'information est due à Shannon (vers 1948), avec bien sûr
l'influence des grands théoriciens de l'informatique (Turing, von
Neumann, Wiener). À noter des convergences avec les travaux de Fisher.
Le problème est celui de la communication entre une source et un
récepteur : la source émet un message que le récepteur lit. On voudrait
quantifier l'« information » que contient chaque message émis.
Par exemple, il est clair que si l'émetteur dit toujours la même chose,
la quantité d'information apportée par une répétition supplémentaire est
nulle.
Le cas le plus simple est le suivant : le récepteur attend une
information de type oui/non, le oui et le non étant a priori
aussi vraisemblables l'un que l'autre. Lorsque la source transmet soit un
oui soit un non, on considère que le récepteur reçoit
une unité d'information (un bit). Autrement dit : une unité
d'information, c'est quand on a a priori un ensemble de deux
possibilités, et que l'une d'elles se réalise.
L'entropie existe en version combinatoire, en version de probabilités
discrètes ou encore en probabilités continues (ce dernier thème étant
très proche de problématiques d'analyse). On commence par la première.
Information combinatoire
Que se passe-t-il si on a plus de possibilités ? Supposons d'abord qu'on
a un ensemble de possibilités 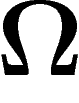 , et que le message consiste à spécifier
un élément de
, et que le message consiste à spécifier
un élément de 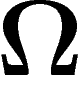 . Si tous les éléments de
. Si tous les éléments de 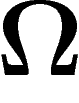 sont aussi
vraisemblables a priori (on verra ci-dessous ce qui se passe si on dote
sont aussi
vraisemblables a priori (on verra ci-dessous ce qui se passe si on dote
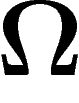 d'une probabilité), quelle est l'information transmise par le
message « telle possibilité s'est réalisée » ?
d'une probabilité), quelle est l'information transmise par le
message « telle possibilité s'est réalisée » ?
Si 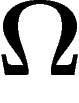 a deux éléments, on transmet une information d'une unité. Si
a deux éléments, on transmet une information d'une unité. Si
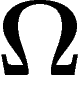 comporte
comporte 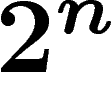 éléments, on peut spécifier un élément de
éléments, on peut spécifier un élément de
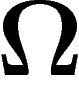 en donnant n informations élémentaires (par exemple par
dichotomie de type « moitié de droite / moitié de gauche » ou bien en
numérotant les éléments de
en donnant n informations élémentaires (par exemple par
dichotomie de type « moitié de droite / moitié de gauche » ou bien en
numérotant les éléments de 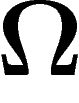 et en donnant la décomposition en
base
et en donnant la décomposition en
base  ). On a donc envie de dire que spécifier un élément parmi un
ensemble
). On a donc envie de dire que spécifier un élément parmi un
ensemble 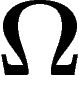 de possibilités revient à transmettre
de possibilités revient à transmettre 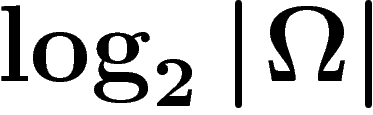 unités d'information. (Désormais dans cette partie, tous
les logarithmes seront implicitement pris en base
unités d'information. (Désormais dans cette partie, tous
les logarithmes seront implicitement pris en base  .)
.)
À noter que la quantité d'information n'est pas une propriété intrinsèque
d'un certain objet, mais une propriété de cet objet en relation avec un
ensemble de possibilités dans lequel on considère qu'il se trouve : comme
l'entropie en physique, la quantité d'information est une notion relative
à la connaissance préalable de l'observateur du système, du récepteur du
message.
À ce stade, en notant 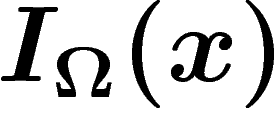 la quantité d'information de
l'événement x appartenant à l'ensemble
la quantité d'information de
l'événement x appartenant à l'ensemble 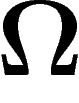 , on a donc
, on a donc
![\[
I_\Omega(x)=\log\abs{\Omega}
\]](entropie016.png)
Avant d'en venir à un cadre probabilisé, regardons quelle est
l'information d'une phrase telle que « l'événement réalisé appartient à
un sous-ensemble A de l'ensemble 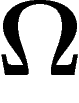 des possibilités ». On
applique le principe intuitif suivant : si on dit que l'événement réalisé
appartient à une partie A, puis qu'on spécifie ensuite de quel
événement de A il s'agit, on a totalement spécifié l'événement, comme
si on l'avait donné directement dès le début. Spécifier directement
l'événement réalisé, c'est transmettre
des possibilités ». On
applique le principe intuitif suivant : si on dit que l'événement réalisé
appartient à une partie A, puis qu'on spécifie ensuite de quel
événement de A il s'agit, on a totalement spécifié l'événement, comme
si on l'avait donné directement dès le début. Spécifier directement
l'événement réalisé, c'est transmettre 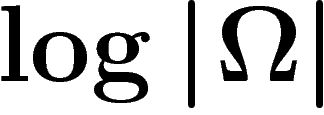 unités
d'information. Spécifier un événement en sachant déjà qu'il appartient à
un sous-ensemble A, peut se faire en transmettant
unités
d'information. Spécifier un événement en sachant déjà qu'il appartient à
un sous-ensemble A, peut se faire en transmettant 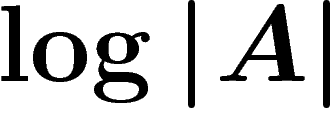 unités d'information. On en déduit qu'en précisant que l'événement
appartient à A, on avait déjà transmis
unités d'information. On en déduit qu'en précisant que l'événement
appartient à A, on avait déjà transmis
 unités d'information d'où
unités d'information d'où
![\[
I_\Omega(A)
=\log\abs{\Omega}/\abs{A}
\]](entropie021.png)
Cadre probabiliste
Supposons maintenant que toutes les possibilités ne sont pas
équiprobables mais qu'on sait que certaines, a priori, apparaîtront plus
souvent que d'autres. L'idée est que les événements plus rares
contiennent plus d'information (exemple : complétez les mots français de
cinq lettres Z___E et E___E).
On peut s'inspirer de la version combinatoire ci-dessus : on sait que
l'appartenance à une partie A dans un ensemble 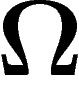 est un
événement de
est un
événement de 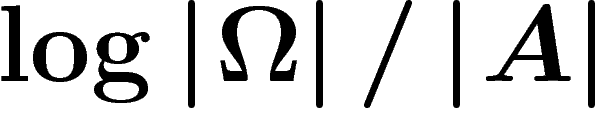 unités d'information. Si on
suppose qu'
unités d'information. Si on
suppose qu'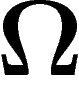 est un ensemble probabilisé où tous les événements
sont équiprobables, la probabilité de la partie A est
est un ensemble probabilisé où tous les événements
sont équiprobables, la probabilité de la partie A est
 ; l'information apportée par la réalisation d'un
événement de A est donc
; l'information apportée par la réalisation d'un
événement de A est donc 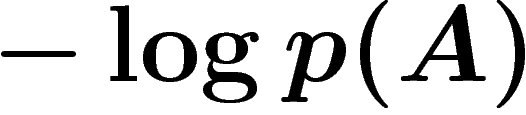 .
.
Si désormais 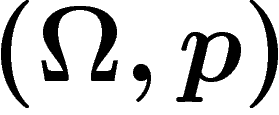 est un espace probabilisé, et
est un espace probabilisé, et  un événement, on pose donc
un événement, on pose donc
![\[
I_\Omega(A)=-\log p(A)
\]](entropie029.png)
et en particulier, pour un élément x
![\[
I_\Omega(x)=-\log p(x)
\]](entropie030.png)
Cette définition a bien la propriété qu'on attendait, à savoir que la
survenue d'un événement rare contient plus d'information. Inversement, la
survenue d'un événement certain (de probabilité  ) n'apporte aucune
information.
) n'apporte aucune
information.
La quantité d'information dépend plus de la distribution de probabilité
que d'un événement x particulier. On va donc définir l'entropie
d'une distribution de probabilité : c'est l'information moyenne qu'on
obtient si on tire un élément de 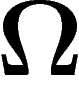 suivant la probabilité p :
suivant la probabilité p :
![\[
S(\Omega, p)=\sum_{x\in\Omega}p(x)I_\Omega(x)=-\sum_{x\in\Omega}p(x)\log
p(x)
\]](entropie033.png)
Revenons au modèle de l'émetteur et du récepteur : on suppose qu'à chaque
instant, l'émetteur envoie une lettre a de l'alphabet avec la
probabilité 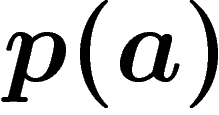 ; l'entropie est alors la quantité moyenne
d'information apportée par chaque nouvelle lettre transmise, ou encore,
l'incertitude moyenne sur la prochaine lettre qui va arriver.
; l'entropie est alors la quantité moyenne
d'information apportée par chaque nouvelle lettre transmise, ou encore,
l'incertitude moyenne sur la prochaine lettre qui va arriver.
L'entropie est maximale quand toutes les possibilités sont a priori
équiprobables ; s'il y a n possibilités, l'entropie est alors 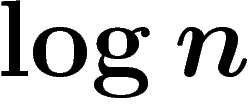 .
Inversement, si la mesure est concentrée en un point de probabilité
.
Inversement, si la mesure est concentrée en un point de probabilité  ,
alors un tirage sous cette loi n'apporte aucune information car le
résultat est connu d'avance, l'entropie est nulle.
,
alors un tirage sous cette loi n'apporte aucune information car le
résultat est connu d'avance, l'entropie est nulle.
L'entropie d'une loi de probabilité est ainsi une mesure de sa
dispersion.
La formule ci-dessus est celle obtenue par Boltzmann (à un facteur k près, la
constante de Boltzmann, qui est un changement de l'unité d'information)
pour la thermodynamique : Boltzmann suppose qu'on a un système composé de
N particules indiscernables, et on sait que la proportion de particules
se trouvant dans l'état i est 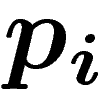 . Quelle est la quantité
d'information apportée par la spécification complète de l'état
microscopique des particules, autrement dit, la liste qui pour chaque
particules dit dans quel état elle se trouve ? Le nombre de possibilités
de répartir les N particules en respectant les proportions est
. Quelle est la quantité
d'information apportée par la spécification complète de l'état
microscopique des particules, autrement dit, la liste qui pour chaque
particules dit dans quel état elle se trouve ? Le nombre de possibilités
de répartir les N particules en respectant les proportions est
![\[
\abs{\Omega}=\frac{N!}{(p_1N)! \,(p_2N)!\ldots (p_kN)!}
\]](entropie038.png)
et la quantité d'information moyenne par particule est
![\[S=\frac1N \log\abs{\Omega}\sim -\sum p_i\log p_i
\]](entropie039.png)
quand N est grand. (On a simplement utilisé 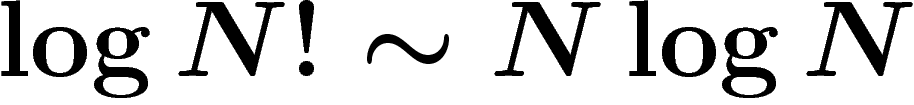 .)
.)
Si toutes les probabilités sont égales à 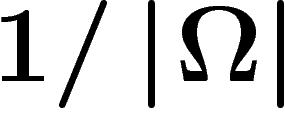 , on trouve en
particulier la formule célèbre
, on trouve en
particulier la formule célèbre 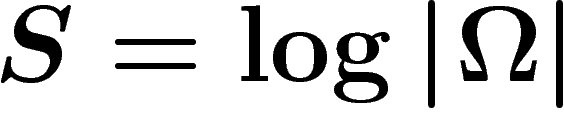 qui (avec la
constante de proportionnalité k) est gravée sur la tombe de Boltzmann.
Dans ce cas, l'entropie de la distribution de probabilité est bien sûr
égale à la quantité d'information apportée par chaque événement
particulier. (Ce qui est à l'origine d'un certain nombre de confusions,
du fait que l'entropie est une notion globale définie pour une mesure de
probabilité, et que parler de l'entropie d'un état particulier n'a pas de
sens. En physique, l'entropie d'un état macroscopique donné est en fait
l'entropie de la mesure uniforme sur tous les états microscopiques
donnant cet état macroscopique.)
qui (avec la
constante de proportionnalité k) est gravée sur la tombe de Boltzmann.
Dans ce cas, l'entropie de la distribution de probabilité est bien sûr
égale à la quantité d'information apportée par chaque événement
particulier. (Ce qui est à l'origine d'un certain nombre de confusions,
du fait que l'entropie est une notion globale définie pour une mesure de
probabilité, et que parler de l'entropie d'un état particulier n'a pas de
sens. En physique, l'entropie d'un état macroscopique donné est en fait
l'entropie de la mesure uniforme sur tous les états microscopiques
donnant cet état macroscopique.)
Tous ces raisonnements intuitifs sont justifiés par le théorème suivant,
dû à Shannon, sans doute le premier théorème de théorie de
l'information :
Le dernier axiome est un axiome de regroupement, qu'on avait déjà utilisé
ci-dessus pour calculer la quantité d'information apportée par une partie
 . Supposons par exemple que le message soit constitué de
lettres, mais qu'on confonde les lettres E et F. Alors la quantité
d'information reçue à la transmission est seulement
. Supposons par exemple que le message soit constitué de
lettres, mais qu'on confonde les lettres E et F. Alors la quantité
d'information reçue à la transmission est seulement 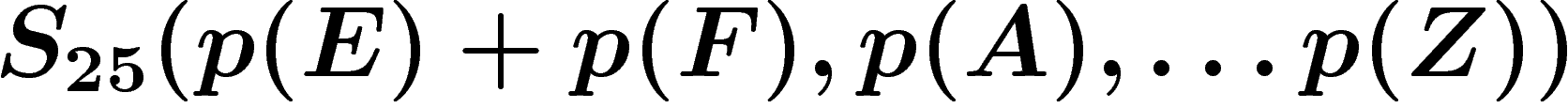 et pour reconstituer le message, il faut, dans une proportion
et pour reconstituer le message, il faut, dans une proportion
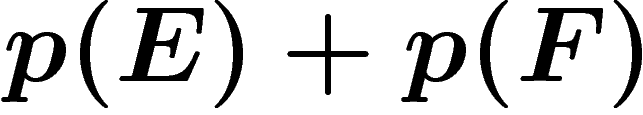 des cas, demander une information supplémentaire qui
départage entre E et F, ce qui transmet exactement
des cas, demander une information supplémentaire qui
départage entre E et F, ce qui transmet exactement
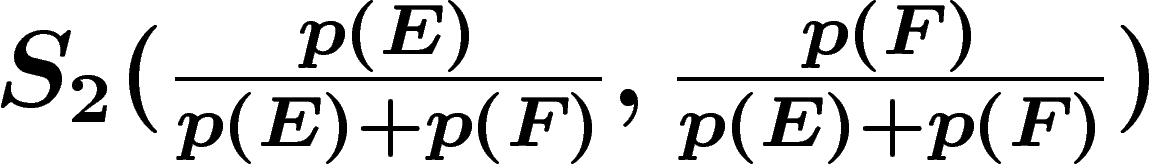 unités
d'information.
unités
d'information.
Entropie d'une suite de variables
Si X et Y sont deux variables aléatoires, on peut définir l'entropie
du couple 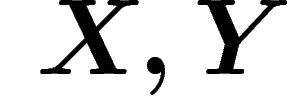 :
: 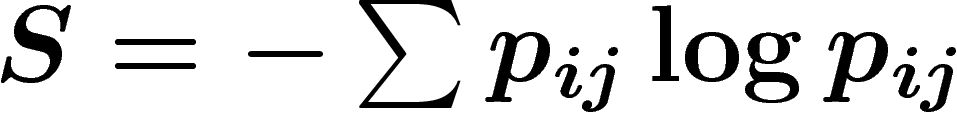 . On peut bien sûr généraliser
à un nombre quelconque de variables.
. On peut bien sûr généraliser
à un nombre quelconque de variables.
Il résulte de la définition que si X et Y sont deux variables aléatoires
indépendantes, on a
![\[
S(X,Y)=S(X)+S(Y)
\]](entropie053.png)
autrement dit, pour des variables indépendantes, l'information conjointe
est égale à la somme des informations.
Ceci n'est pas toujours vrai : il se peut que la variable X contienne
de l'information sur ce que va être Y.
Par exemple, si on répète toujours deux fois de suite la même chose,
l'information de la deuxième répétition est nulle : 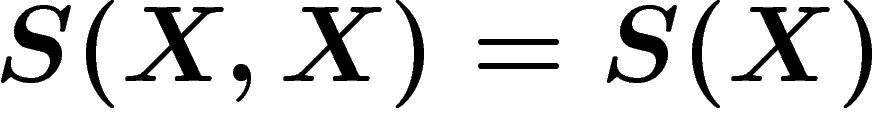 . En
fait on a toujours
. En
fait on a toujours
![\[
S(X,Y)\leq S(X)+S(Y)
\]](entropie055.png)
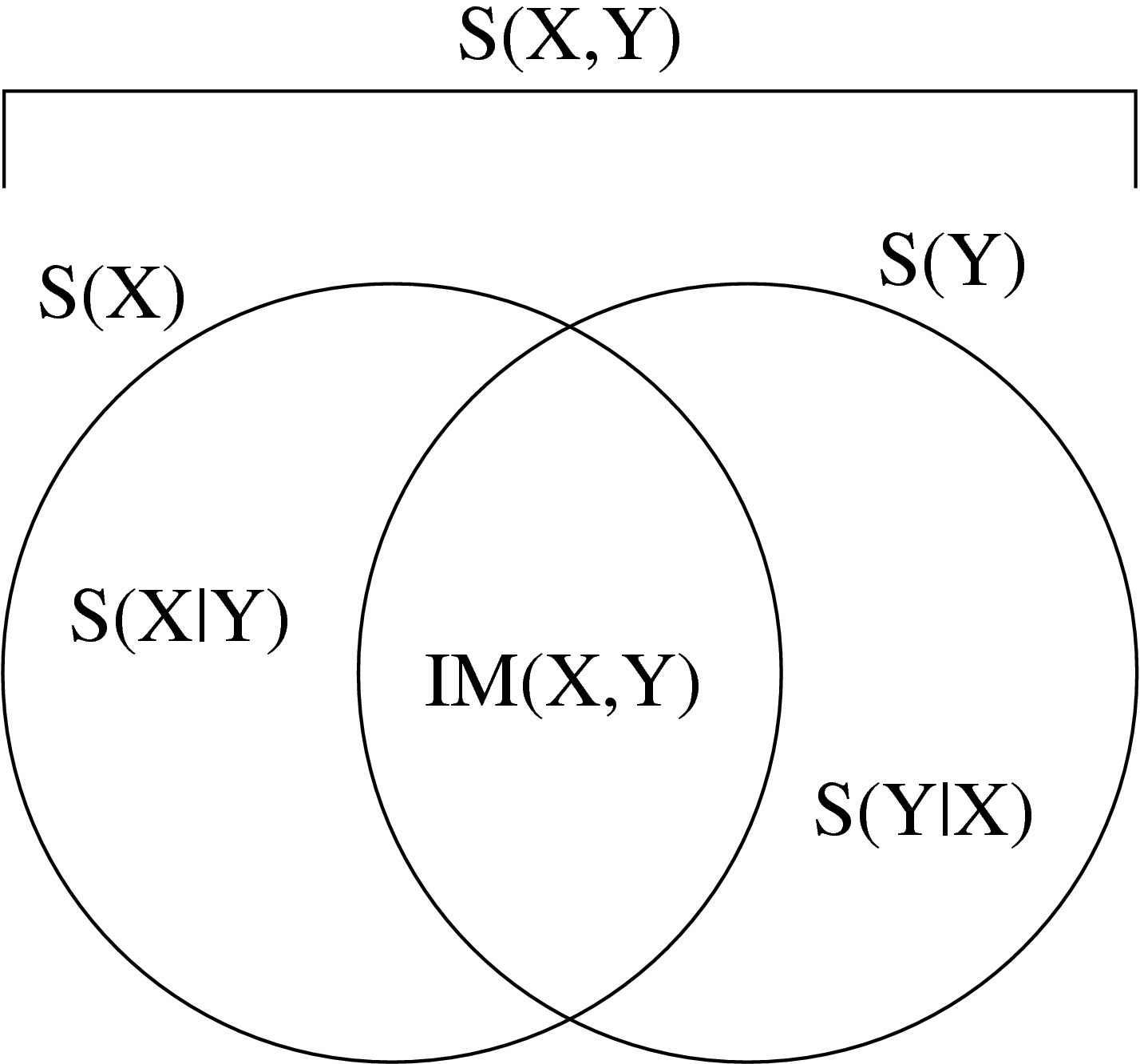
avec égalité si et seulement si X et Y sont indépendants. Ceci peut
servir par exemple à définir une information partielle
![\[S(Y|X)=S(X,Y)-S(X)
\]](entropie056.png)
c'est la quantité d'information réellement apportée
par Y si on connaît déjà X, ainsi qu'une information mutuelle
![\[
I\!M(X,Y)=S(X)+S(Y)-S(X,Y)
\]](entropie057.png)
c'est la quantité d'information présente « en double » dans X et
dans Y.
Revenons à une source qui émet régulièrement des signaux. Soit 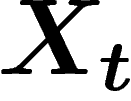 le
signal émis au temps t, c'est une variable aléatoire à valeurs dans un
certain alphabet. Ces variables ne sont pas forcément indépendantes (cas
d'un texte en français : chaque lettre dépend des précédentes).
L'entropie de la suite infinie
le
signal émis au temps t, c'est une variable aléatoire à valeurs dans un
certain alphabet. Ces variables ne sont pas forcément indépendantes (cas
d'un texte en français : chaque lettre dépend des précédentes).
L'entropie de la suite infinie  est définie
par
est définie
par
![\[
S(X)=\lim_{n\rightarrow \infty} \frac1n S(X_1,\ldots,X_n)
\]](entropie061.png)
si cette limite existe, où 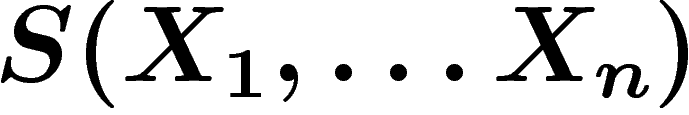 est l'entropie de la
distribution jointe du n-uplet
est l'entropie de la
distribution jointe du n-uplet  .
.
Si les lettres successives du message sont toutes indépendantes et
équidistribuées (la loi de 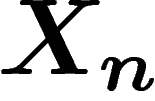 est égale à la loi de
est égale à la loi de
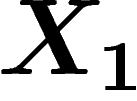 pour tout n), alors on a bien sûr
pour tout n), alors on a bien sûr
![\[
S(X_1,\ldots,X_n,\ldots)=\lim \frac1n S(X_1,\ldots,X_n)=S(X_1)
\]](entropie066.png)
Autrement dit, dans le cas d'une source qui émet des lettres
successives et indépendantes toujours avec la même loi, la quantité
d'information moyenne pour chaque nouvelle lettre, est égale à l'entropie
de la loi.
Entropie et codages
Codage sans bruit
La base des définitions ci-dessus était la constatation qu'un élément
d'un ensemble de taille 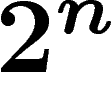 peut être codé par n unités
d'information. C'est le premier lien entre théorie de l'information et
codage.
peut être codé par n unités
d'information. C'est le premier lien entre théorie de l'information et
codage.
Un codage sur un alphabet A est une application
injective de A vers l'ensemble des mots sur un alphabet B (souvent
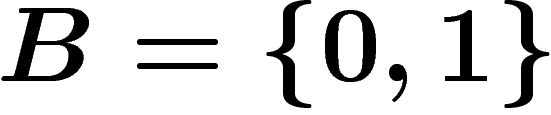 ). On dit que le codage est instantanément décodable
s'il n'existe pas deux lettres
). On dit que le codage est instantanément décodable
s'il n'existe pas deux lettres 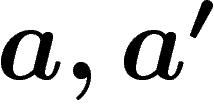 de A telles que le code de a
soit un préfixe du code de
de A telles que le code de a
soit un préfixe du code de 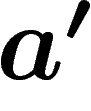 . Tous les codages ci-dessous seront
supposés instantanément décodables.
. Tous les codages ci-dessous seront
supposés instantanément décodables.
On étend le codage aux mots sur A par concaténation des codes des
lettres. La propriété d'être instantanément décodable garantit alors que
le codage des mots est non ambigu.
Le problème est le plus souvent de trouver les codages les plus courts
possibles. La stratégie de base consiste à attribuer des codes courts aux
lettres fréquentes, et des codes longs aux lettres moins fréquentes.
Soient 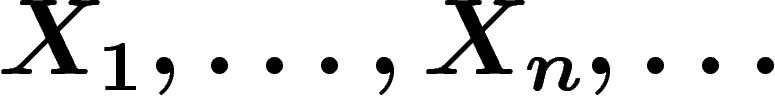 des variables aléatoires identiquement
distribuées à valeurs dans un ensemble A. Soit C un codage de A
utilisant un alphabet B. On définit la longueur moyenne du codage :
des variables aléatoires identiquement
distribuées à valeurs dans un ensemble A. Soit C un codage de A
utilisant un alphabet B. On définit la longueur moyenne du codage :
![\[
L(C)=\lim_n \frac1n \mathbb{E} \ell (C(X_1\ldots X_n))
\]](entropie072.png)
où 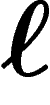 représente la longueur d'un mot sur l'alphabet B. On a alors
le théorème de codage de Shannon, qui identifie entropie et taux de
compression maximal :
représente la longueur d'un mot sur l'alphabet B. On a alors
le théorème de codage de Shannon, qui identifie entropie et taux de
compression maximal :
Théorème.
Soit
C un codage instantanément décodable pour la suite de variables
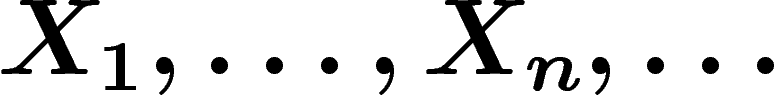
. Alors
![\[
L(C)\geq \frac{S(X_1,\ldots,X_n,\ldots)}{\log \abs{B}}
\]](entropie075.png)
De plus, on peut construire des codages ayant des longueurs
arbitrairement proches de cette valeur.
La preuve qu'aucun code ne fait mieux que cette valeur est simple :
c'est essentiellement le fait que si 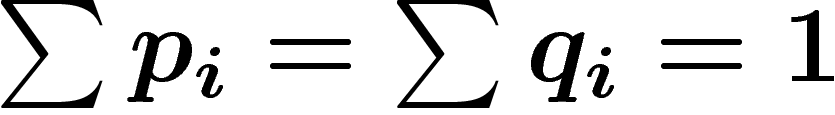 , alors
, alors 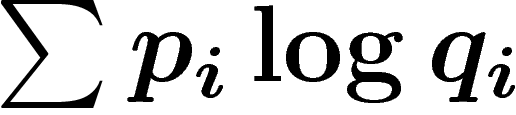 est maximal quand
est maximal quand 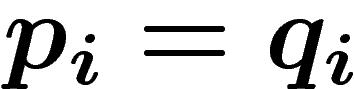 , et la
remarque que si les
, et la
remarque que si les 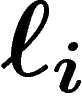 sont les longueurs des codes d'un codage
instantanément déchiffrable, on a
sont les longueurs des codes d'un codage
instantanément déchiffrable, on a 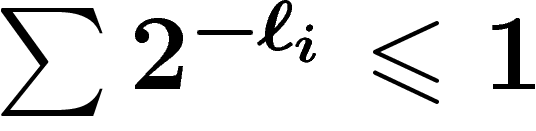 .
.
L'idée de la preuve que l'optimum peut être approché est la suivante :
les mots de longueur n obtenus par tirage des 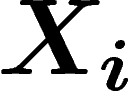 peuvent être
décomposés en deux classes, une classe de mots « typiques » et une
classe de mots « rares ». Les mots typiques sont environ au nombre de
peuvent être
décomposés en deux classes, une classe de mots « typiques » et une
classe de mots « rares ». Les mots typiques sont environ au nombre de
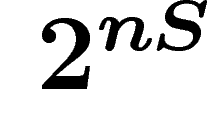 , chacun d'entre eux étant de probabilité environ
, chacun d'entre eux étant de probabilité environ 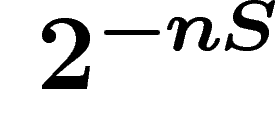 ; les
mots rares ont une probabilité totale négligeable. Pour coder dans
; les
mots rares ont une probabilité totale négligeable. Pour coder dans
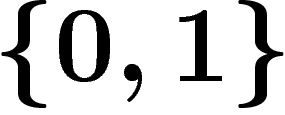 un mot typique, on met un « 0 » suivi du code en base
un mot typique, on met un « 0 » suivi du code en base  du
numéro du mot typique parmi les
du
numéro du mot typique parmi les 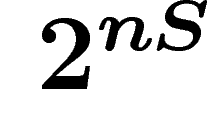 mots typiques (ce qui prend nS
chiffres en base
mots typiques (ce qui prend nS
chiffres en base  ) ; pour un mot rare, on met un « 1 » suivi
simplement du code en base
) ; pour un mot rare, on met un « 1 » suivi
simplement du code en base  du numéro du mot rare parmi l'ensemble des
mots possibles sur l'alphabet de départ.
du numéro du mot rare parmi l'ensemble des
mots possibles sur l'alphabet de départ.
Un codage plus simple, proche du codage optimal, est le codage de
Shannon-Fano : il consiste à attribuer à la lettre a un code en base
 de longueur
de longueur 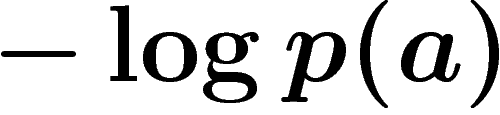 (arrondi à l'entier supérieur), ce qui est
toujours possible : par exemple, arranger les probabilités de manière
croissante sur l'intervalle
(arrondi à l'entier supérieur), ce qui est
toujours possible : par exemple, arranger les probabilités de manière
croissante sur l'intervalle ![$[0;1]$](entropie091.png) , ce qui donne une partition en
sous-intervalles, si un intervalle est de longueur
, ce qui donne une partition en
sous-intervalles, si un intervalle est de longueur 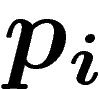 on peut trouver
un nombre binaire à
on peut trouver
un nombre binaire à 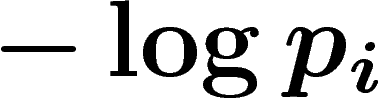 chiffres qu'on lui associe, de manière à
former un codage sans préfixes. Autrement dit on code les lettres plus
fréquentes par des mots plus courts.
chiffres qu'on lui associe, de manière à
former un codage sans préfixes. Autrement dit on code les lettres plus
fréquentes par des mots plus courts.
Codage avec bruit
On s'intéresse désormais au codage par des canaux de communication qui
peuvent introduire des erreurs. Soit X le message à la source, Z le
message codé transmis dans un canal (qui est une fonction aléatoire de
X). Soit  une fonction de
décodage, on veut que
une fonction de
décodage, on veut que 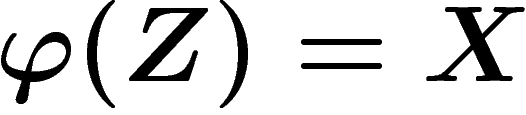 le plus souvent possible, mais le
passage de X vers Z n'est pas forcément injectif. Le théorème
suivant, dû à Fano, affirme que la probabilité minimale d'erreur est liée
à l'entropie :
le plus souvent possible, mais le
passage de X vers Z n'est pas forcément injectif. Le théorème
suivant, dû à Fano, affirme que la probabilité minimale d'erreur est liée
à l'entropie :
Théorème.
Pour toute fonction de décodage

, la probabilité que
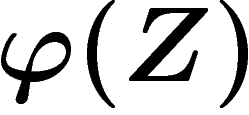
soit
différent de
X est supérieure ou égale à
![\[
\frac{S(X|Z)-1}{\log\abs{X}}
\]](entropie098.png)
où
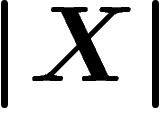
est la taille de l'alphabet de
X.
Un canal de communication binaire étant donné, avec des probabilités
d'erreur, il y a un arbitrage à faire entre concision du codage et
probabilité de décodage correct : si on prend un codage sans aucune
redondance, le décodage est très sensible à toute erreur ; si on répète
trois fois chaque mot, on a de meilleures chances d'être compris.
Supposons donc qu'un émetteur fait transiter une lettre X d'un alphabet
A au travers d'un canal binaire  . Auparavant, il code X par une
suite binaire Y de longueur
. Auparavant, il code X par une
suite binaire Y de longueur 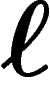 . Le récepteur, lui, reçoit à la
sortie du canal une suite binaire Z qui est une fonction aléatoire
de la suite binaire Y donnée à l'entrée du canal.
. Le récepteur, lui, reçoit à la
sortie du canal une suite binaire Z qui est une fonction aléatoire
de la suite binaire Y donnée à l'entrée du canal.
On définit la capacité d'un canal  par
par
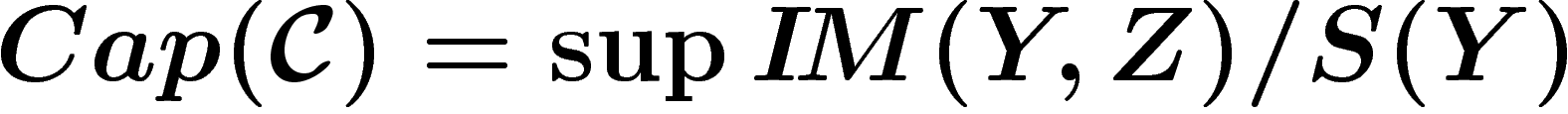 , le sup étant pris sur toutes les
lois de probabilité possibles pour le mot binaire Y. Cette quantité ne
dépend que du canal.
, le sup étant pris sur toutes les
lois de probabilité possibles pour le mot binaire Y. Cette quantité ne
dépend que du canal.
Par exemple, imaginons que le canal transmette des  et des
et des  , mais,
avec une faible probabilité p, change un
, mais,
avec une faible probabilité p, change un  en
en  ou un
ou un  en
en  .
La capacité est alors
.
La capacité est alors 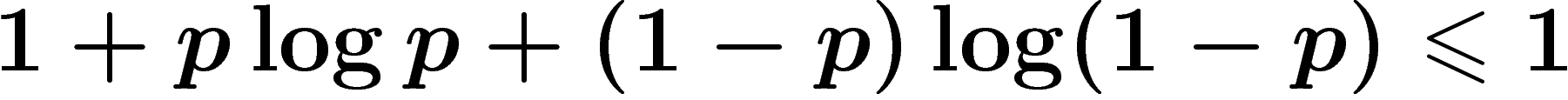 . Dans le cas où
. Dans le cas où
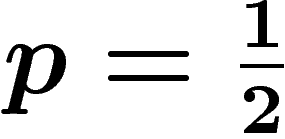 , aucune information ne peut être tirée, la capacité est
nulle.
, aucune information ne peut être tirée, la capacité est
nulle.
Un canal étant donné, on peut se demander quel codage adopter. Soit A
l'alphabet de départ, un codage binaire est une application
 pour une certaine longueur
pour une certaine longueur 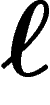 (pour
simplifier, on considère des codages à longueur constante). On définit
la probabilité d'erreur
(pour
simplifier, on considère des codages à longueur constante). On définit
la probabilité d'erreur 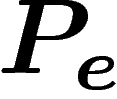 d'un codage C (avec fonction de décodage
D) par
d'un codage C (avec fonction de décodage
D) par 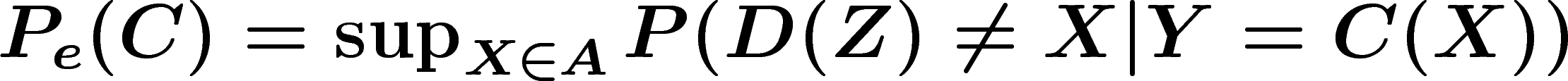 . On définit aussi le
taux de compression du codage par
. On définit aussi le
taux de compression du codage par 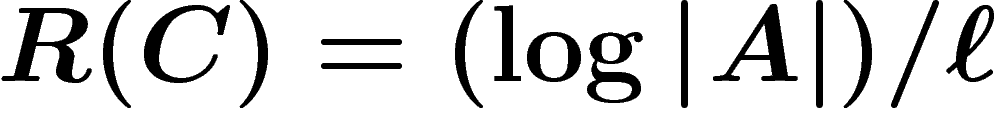 .
.
Shannon montre alors le théorème suivant, qui identifie la capacité du
canal avec le taux de compression optimal :
Théorème.
La capacité
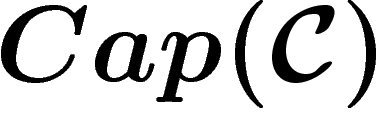
d'un canal

est
égale au sup des nombres
R tels que, pour tout
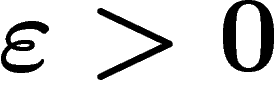
, il existe un
alphabet
A, une longueur
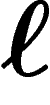
, un codage

tels que
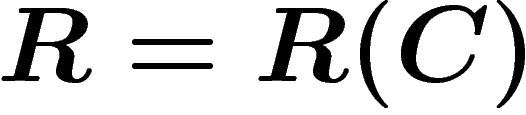
et
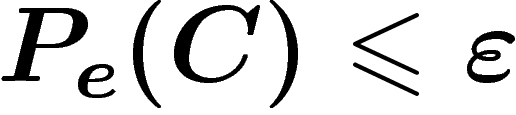
.
La preuve de ce théorème est hautement non constructive (on choisit le
codage au hasard!), et comme ci-dessus elle utilise des mots
« typiques ». Ce domaine de recherche est encore très ouvert.
Codage continu
On s'intéresse désormais à la situation où on cherche à transmettre une
quantité continue (intensité, voltage...). Cette fois-ci on a donc des
lois de probabilité sur 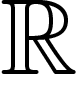 . Par analogie avec le cas discret,
l'entropie d'une distribution de probabilité f sur
. Par analogie avec le cas discret,
l'entropie d'une distribution de probabilité f sur 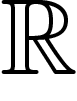 est égale à
est égale à
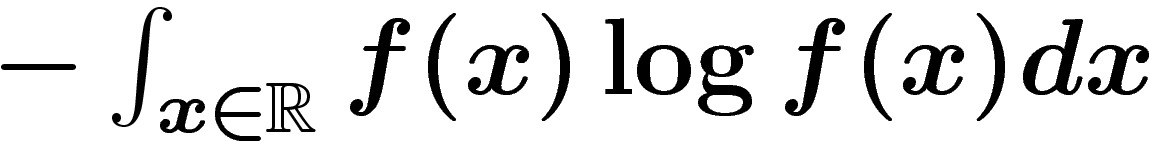 .
.
On remarque que, si on multiplie par c la variable transmise par le
canal, on ajoute 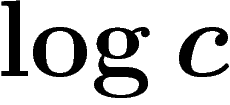 à l'entropie de l'information transmise (ce qui
est naturel : en multipliant par
à l'entropie de l'information transmise (ce qui
est naturel : en multipliant par  on a une précision deux fois plus
grande, ce qui donne un bit d'information en plus). Pour
obtenir des résultats pertinents, on suppose en général que les canaux
utilisés sont limités en puissance, par exemple qu'ils ne peuvent pas
transmettre une variable dont la variance est supérieure à un certain
seuil (sans cette hypothèse, on peut facilement transmettre une quantité
infinie d'information).
on a une précision deux fois plus
grande, ce qui donne un bit d'information en plus). Pour
obtenir des résultats pertinents, on suppose en général que les canaux
utilisés sont limités en puissance, par exemple qu'ils ne peuvent pas
transmettre une variable dont la variance est supérieure à un certain
seuil (sans cette hypothèse, on peut facilement transmettre une quantité
infinie d'information).
Un simple calcul variationnel montre que, parmi les distributions de
probabilité de variance fixée, les gaussiennes sont celles d'entropie
maximale. En effet, soit f une fonction maximisant 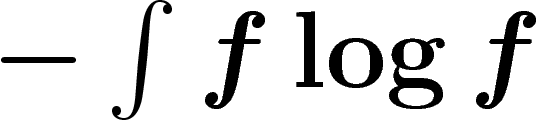 , et
calculons l'entropie d'une fonction voisine
, et
calculons l'entropie d'une fonction voisine 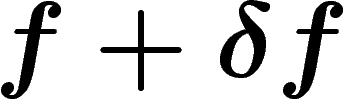 de même
variance. Comme
de même
variance. Comme 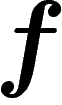 et
et 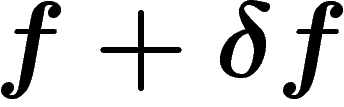 sont des mesures de probabilité,
donc d'intégrale
sont des mesures de probabilité,
donc d'intégrale  , on a
, on a 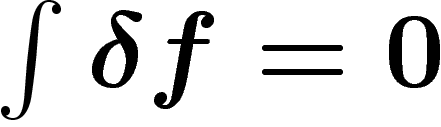 . On peut supposer que f et
. On peut supposer que f et
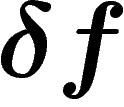 sont de moyenne nulle (par translation), et donc
sont de moyenne nulle (par translation), et donc 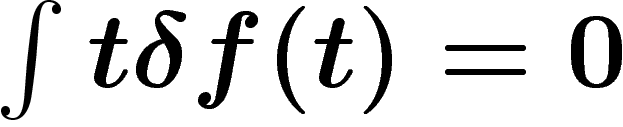 . Alors le fait que
. Alors le fait que 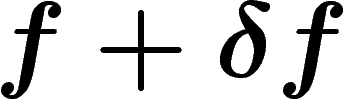 ait même variance que f
s'écrit
ait même variance que f
s'écrit 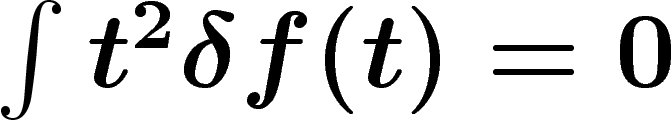 . Maintenant, la variation d'entropie est
. Maintenant, la variation d'entropie est
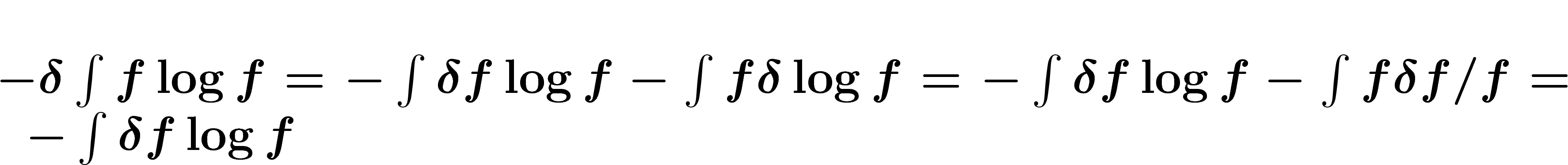 . Pour tout
. Pour tout
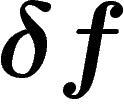 vérifiant
vérifiant 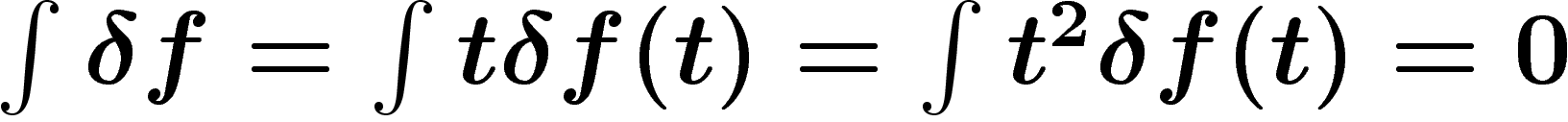 , on doit donc avoir
, on doit donc avoir 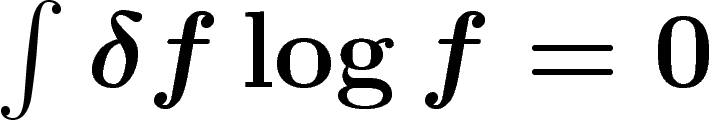 si f est un
extrémum d'entropie. Cela implique
si f est un
extrémum d'entropie. Cela implique 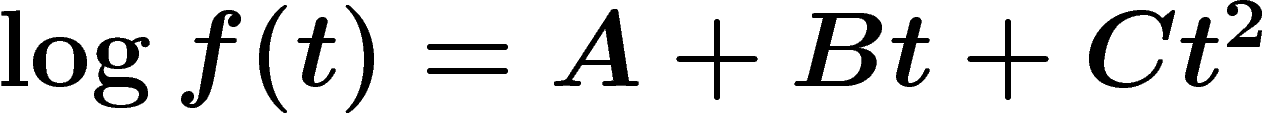 , d'où la
gaussienne.
, d'où la
gaussienne.
Intéressons-nous au cas où on cherche à transmettre une information X à
travers un canal limité en puissance, la limite étant p (autrement dit
l'espérance de 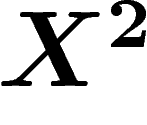 doit être inférieure à p). Mais ce canal est
bruité ; plus exactement, on a un ennemi qui a accès à ce canal et qui
peut transmettre du bruit Y (indépendant de X), la puissance du bruit
transmis étant inférieure à
doit être inférieure à p). Mais ce canal est
bruité ; plus exactement, on a un ennemi qui a accès à ce canal et qui
peut transmettre du bruit Y (indépendant de X), la puissance du bruit
transmis étant inférieure à 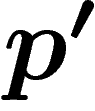 . Le récepteur reçoit
. Le récepteur reçoit 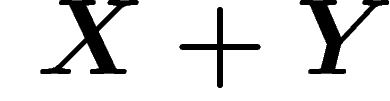 , qui fait
perdre de l'information par rapport à X. Ce qui intéresse le
transmetteur est de maximiser
, qui fait
perdre de l'information par rapport à X. Ce qui intéresse le
transmetteur est de maximiser 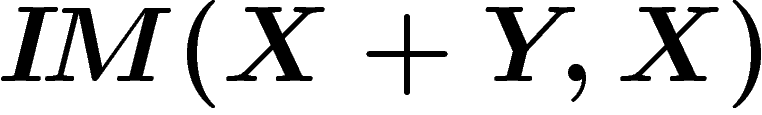 à Y donné, tandis que
l'ennemi cherche à minimiser cette quantité à X donné (si chacun
connaît la stratégie appliquée par l'autre).
à Y donné, tandis que
l'ennemi cherche à minimiser cette quantité à X donné (si chacun
connaît la stratégie appliquée par l'autre).
Théorème.
Il y a un équilibre de Nash à ce jeu, qui vérifie :
![\[
\inf_Y\sup_X I\!M(X+Y,X)=\sup_X\inf_Y I\!M(X+Y,X)=\frac12\log(1+\frac{p}{p'})
\]](entropie148.png)
et cet équilibre consiste pour chacun à utiliser des variables
gaussiennes de variances
p et
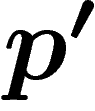
.
À noter que même si 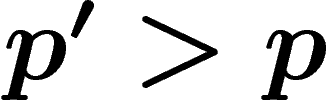 , il reste encore quelque chose du message
initial.
, il reste encore quelque chose du message
initial.
La preuve utilise des inégalités fines. Par analogie avec le fait que les
variances de variables indépendantes s'ajoutent, on définit la
puissance-entropie 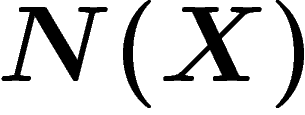 d'une variable X comme la variance qu'aurait
une gaussienne de même entropie que X. (On vérifie qu'en dimension d,
on a
d'une variable X comme la variance qu'aurait
une gaussienne de même entropie que X. (On vérifie qu'en dimension d,
on a 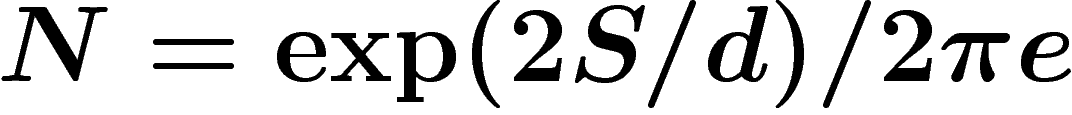 .)
.)
On a alors l'inégalité de puissance-entropie
de Shannon pour des variables indépendantes : 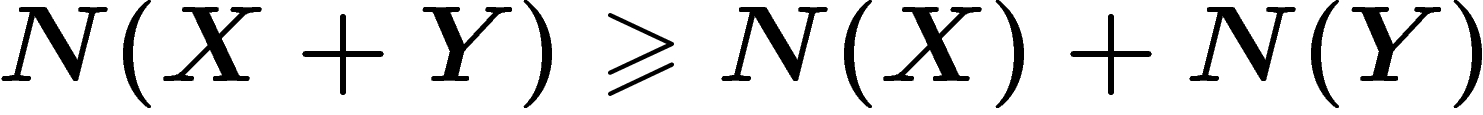 .
Pour conserver l'information on doit monter en puissance... Autre forme
équivalente :
pour
.
Pour conserver l'information on doit monter en puissance... Autre forme
équivalente :
pour 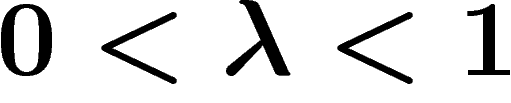 , si X et Y sont des
variables aléatoires indépendantes, alors
, si X et Y sont des
variables aléatoires indépendantes, alors
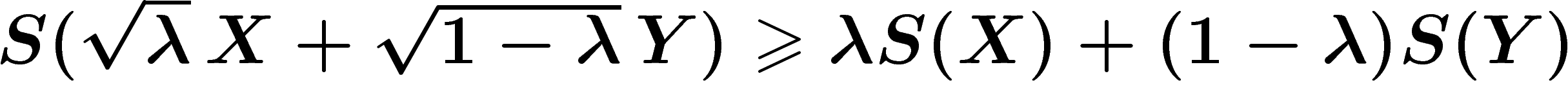 . Ceci peut servir à montrer par exemple que si
. Ceci peut servir à montrer par exemple que si
 sont des variables aléatoires indépendantes
identiquement distribuées, alors
sont des variables aléatoires indépendantes
identiquement distribuées, alors  ressemble à
une gaussienne (au moins si n est une puissance de
ressemble à
une gaussienne (au moins si n est une puissance de  )...
)...
Ces inégalités n'ont pas été rigoureusement démontrées par Shannon (elles
le sont désormais). Elles
sont à rapprocher, par exemple, de l'inégalité de Brunn-Minkowski, ou
encore à des problèmes de constantes optimales dans l'inégalité de
convolution de Young 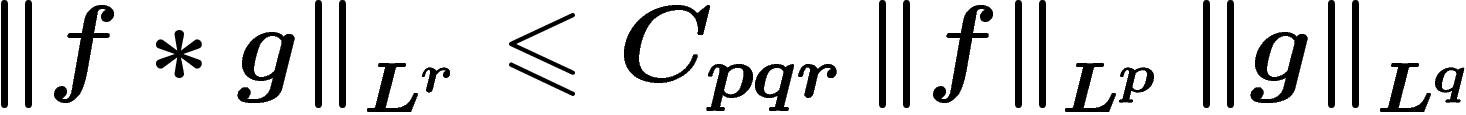 pour
pour 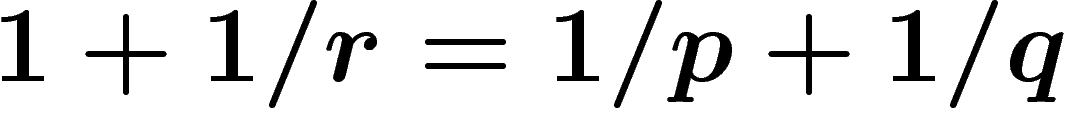 ...
...
Le sujet est donc loin d'être clos.
Back to: Main Page > Mathématiques > Aspects de l'entropie en mathématiques
To leave a comment: contact (domain) yann-ollivier.org
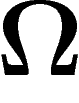 , et que le message consiste à spécifier
un élément de
, et que le message consiste à spécifier
un élément de 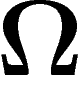 . Si tous les éléments de
. Si tous les éléments de 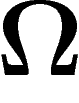 sont aussi
vraisemblables a priori (on verra ci-dessous ce qui se passe si on dote
sont aussi
vraisemblables a priori (on verra ci-dessous ce qui se passe si on dote
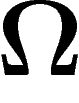 d'une probabilité), quelle est l'information transmise par le
message « telle possibilité s'est réalisée » ?
d'une probabilité), quelle est l'information transmise par le
message « telle possibilité s'est réalisée » ?
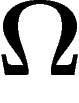 a deux éléments, on transmet une information d'une unité. Si
a deux éléments, on transmet une information d'une unité. Si
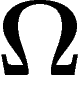 comporte
comporte 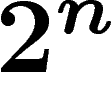 éléments, on peut spécifier un élément de
éléments, on peut spécifier un élément de
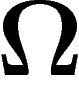 en donnant n informations élémentaires (par exemple par
dichotomie de type « moitié de droite / moitié de gauche » ou bien en
numérotant les éléments de
en donnant n informations élémentaires (par exemple par
dichotomie de type « moitié de droite / moitié de gauche » ou bien en
numérotant les éléments de 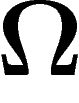 et en donnant la décomposition en
base
et en donnant la décomposition en
base  ). On a donc envie de dire que spécifier un élément parmi un
ensemble
). On a donc envie de dire que spécifier un élément parmi un
ensemble 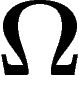 de possibilités revient à transmettre
de possibilités revient à transmettre 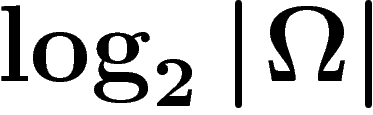 unités d'information. (Désormais dans cette partie, tous
les logarithmes seront implicitement pris en base
unités d'information. (Désormais dans cette partie, tous
les logarithmes seront implicitement pris en base  .)
.)
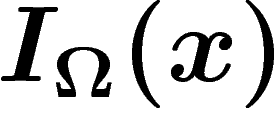 la quantité d'information de
l'événement x appartenant à l'ensemble
la quantité d'information de
l'événement x appartenant à l'ensemble  , on a donc
, on a donc
![\[
I_\Omega(x)=\log\abs{\Omega}
\]](entropie016.png)
 des possibilités ». On
applique le principe intuitif suivant : si on dit que l'événement réalisé
appartient à une partie A, puis qu'on spécifie ensuite de quel
événement de A il s'agit, on a totalement spécifié l'événement, comme
si on l'avait donné directement dès le début. Spécifier directement
l'événement réalisé, c'est transmettre
des possibilités ». On
applique le principe intuitif suivant : si on dit que l'événement réalisé
appartient à une partie A, puis qu'on spécifie ensuite de quel
événement de A il s'agit, on a totalement spécifié l'événement, comme
si on l'avait donné directement dès le début. Spécifier directement
l'événement réalisé, c'est transmettre 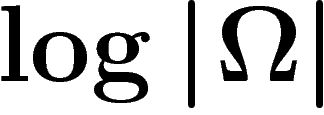 unités
d'information. Spécifier un événement en sachant déjà qu'il appartient à
un sous-ensemble A, peut se faire en transmettant
unités
d'information. Spécifier un événement en sachant déjà qu'il appartient à
un sous-ensemble A, peut se faire en transmettant 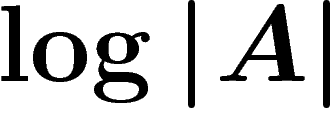 unités d'information. On en déduit qu'en précisant que l'événement
appartient à A, on avait déjà transmis
unités d'information. On en déduit qu'en précisant que l'événement
appartient à A, on avait déjà transmis
 unités d'information d'où
unités d'information d'où
![\[
I_\Omega(A)
=\log\abs{\Omega}/\abs{A}
\]](entropie021.png)
 est un
événement de
est un
événement de 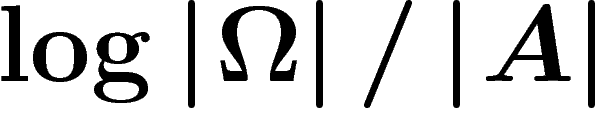 unités d'information. Si on
suppose qu'
unités d'information. Si on
suppose qu'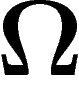 est un ensemble probabilisé où tous les événements
sont équiprobables, la probabilité de la partie A est
est un ensemble probabilisé où tous les événements
sont équiprobables, la probabilité de la partie A est
 ; l'information apportée par la réalisation d'un
événement de A est donc
; l'information apportée par la réalisation d'un
événement de A est donc 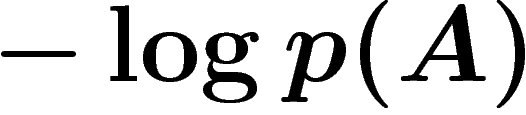 .
.
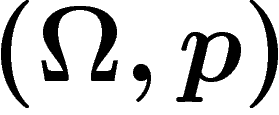 est un espace probabilisé, et
est un espace probabilisé, et  un événement, on pose donc
un événement, on pose donc
![\[
I_\Omega(A)=-\log p(A)
\]](entropie029.png)
![\[
I_\Omega(x)=-\log p(x)
\]](entropie030.png)
 ) n'apporte aucune
information.
) n'apporte aucune
information.
 suivant la probabilité p :
suivant la probabilité p :
![\[
S(\Omega, p)=\sum_{x\in\Omega}p(x)I_\Omega(x)=-\sum_{x\in\Omega}p(x)\log
p(x)
\]](entropie033.png)
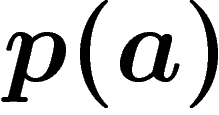 ; l'entropie est alors la quantité moyenne
d'information apportée par chaque nouvelle lettre transmise, ou encore,
l'incertitude moyenne sur la prochaine lettre qui va arriver.
; l'entropie est alors la quantité moyenne
d'information apportée par chaque nouvelle lettre transmise, ou encore,
l'incertitude moyenne sur la prochaine lettre qui va arriver.
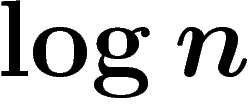 .
Inversement, si la mesure est concentrée en un point de probabilité
.
Inversement, si la mesure est concentrée en un point de probabilité  ,
alors un tirage sous cette loi n'apporte aucune information car le
résultat est connu d'avance, l'entropie est nulle.
,
alors un tirage sous cette loi n'apporte aucune information car le
résultat est connu d'avance, l'entropie est nulle.
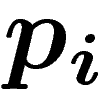 . Quelle est la quantité
d'information apportée par la spécification complète de l'état
microscopique des particules, autrement dit, la liste qui pour chaque
particules dit dans quel état elle se trouve ? Le nombre de possibilités
de répartir les N particules en respectant les proportions est
. Quelle est la quantité
d'information apportée par la spécification complète de l'état
microscopique des particules, autrement dit, la liste qui pour chaque
particules dit dans quel état elle se trouve ? Le nombre de possibilités
de répartir les N particules en respectant les proportions est
![\[
\abs{\Omega}=\frac{N!}{(p_1N)! \,(p_2N)!\ldots (p_kN)!}
\]](entropie038.png)
![\[S=\frac1N \log\abs{\Omega}\sim -\sum p_i\log p_i
\]](entropie039.png)
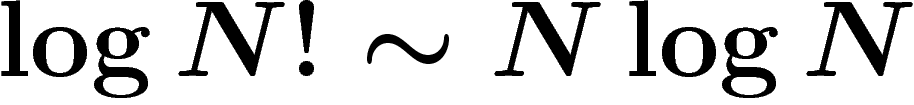 .)
.)
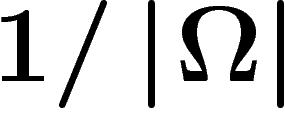 , on trouve en
particulier la formule célèbre
, on trouve en
particulier la formule célèbre 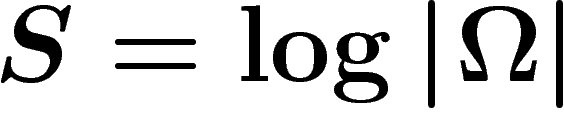 qui (avec la
constante de proportionnalité k) est gravée sur la tombe de Boltzmann.
Dans ce cas, l'entropie de la distribution de probabilité est bien sûr
égale à la quantité d'information apportée par chaque événement
particulier. (Ce qui est à l'origine d'un certain nombre de confusions,
du fait que l'entropie est une notion globale définie pour une mesure de
probabilité, et que parler de l'entropie d'un état particulier n'a pas de
sens. En physique, l'entropie d'un état macroscopique donné est en fait
l'entropie de la mesure uniforme sur tous les états microscopiques
donnant cet état macroscopique.)
qui (avec la
constante de proportionnalité k) est gravée sur la tombe de Boltzmann.
Dans ce cas, l'entropie de la distribution de probabilité est bien sûr
égale à la quantité d'information apportée par chaque événement
particulier. (Ce qui est à l'origine d'un certain nombre de confusions,
du fait que l'entropie est une notion globale définie pour une mesure de
probabilité, et que parler de l'entropie d'un état particulier n'a pas de
sens. En physique, l'entropie d'un état macroscopique donné est en fait
l'entropie de la mesure uniforme sur tous les états microscopiques
donnant cet état macroscopique.)
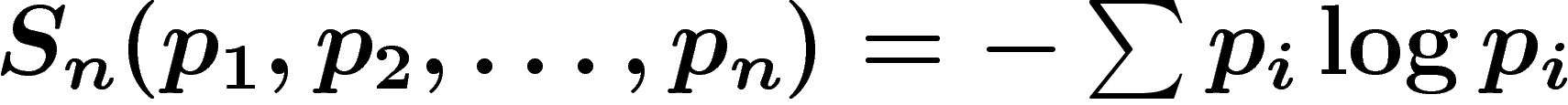 est
la seule vérifiant :
est
la seule vérifiant :
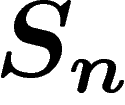 est symétrique en ses arguments, positive, continue
est symétrique en ses arguments, positive, continue
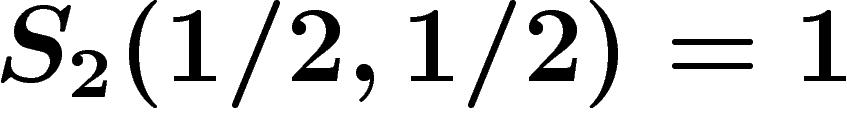
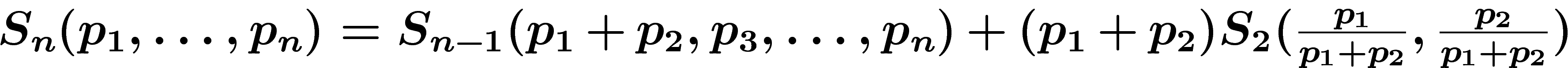
 . Supposons par exemple que le message soit constitué de
lettres, mais qu'on confonde les lettres E et F. Alors la quantité
d'information reçue à la transmission est seulement
. Supposons par exemple que le message soit constitué de
lettres, mais qu'on confonde les lettres E et F. Alors la quantité
d'information reçue à la transmission est seulement 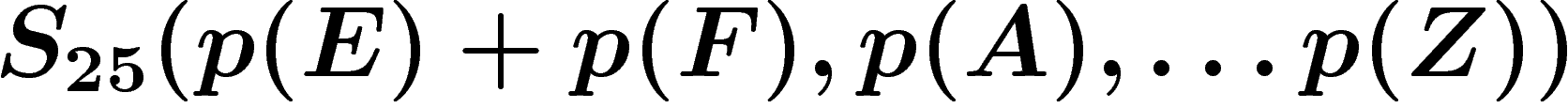 et pour reconstituer le message, il faut, dans une proportion
et pour reconstituer le message, il faut, dans une proportion
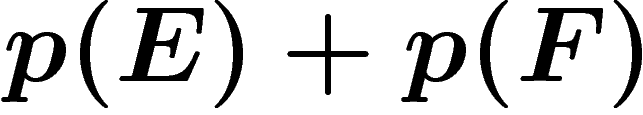 des cas, demander une information supplémentaire qui
départage entre E et F, ce qui transmet exactement
des cas, demander une information supplémentaire qui
départage entre E et F, ce qui transmet exactement
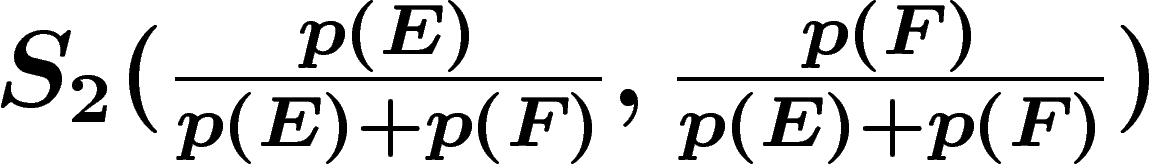 unités
d'information.
unités
d'information.
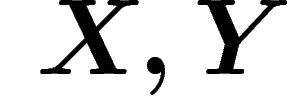 :
: 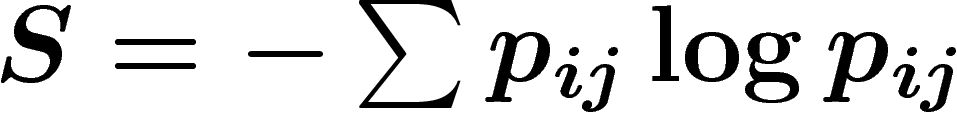 . On peut bien sûr généraliser
à un nombre quelconque de variables.
. On peut bien sûr généraliser
à un nombre quelconque de variables.
![\[
S(X,Y)=S(X)+S(Y)
\]](entropie053.png)
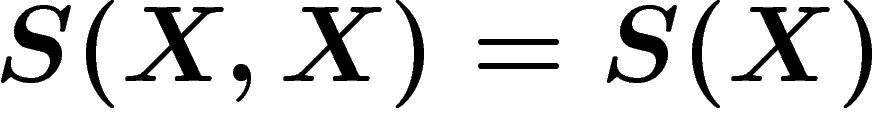 . En
fait on a toujours
. En
fait on a toujours
![\[
S(X,Y)\leq S(X)+S(Y)
\]](entropie055.png)
![\[S(Y|X)=S(X,Y)-S(X)
\]](entropie056.png)
![\[
I\!M(X,Y)=S(X)+S(Y)-S(X,Y)
\]](entropie057.png)

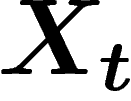 le
signal émis au temps t, c'est une variable aléatoire à valeurs dans un
certain alphabet. Ces variables ne sont pas forcément indépendantes (cas
d'un texte en français : chaque lettre dépend des précédentes).
L'entropie de la suite infinie
le
signal émis au temps t, c'est une variable aléatoire à valeurs dans un
certain alphabet. Ces variables ne sont pas forcément indépendantes (cas
d'un texte en français : chaque lettre dépend des précédentes).
L'entropie de la suite infinie  est définie
par
est définie
par
![\[
S(X)=\lim_{n\rightarrow \infty} \frac1n S(X_1,\ldots,X_n)
\]](entropie061.png)
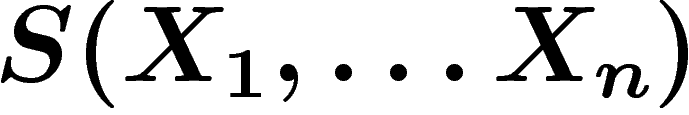 est l'entropie de la
distribution jointe du n-uplet
est l'entropie de la
distribution jointe du n-uplet  .
.
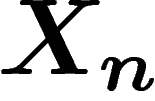 est égale à la loi de
est égale à la loi de
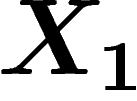 pour tout n), alors on a bien sûr
pour tout n), alors on a bien sûr
![\[
S(X_1,\ldots,X_n,\ldots)=\lim \frac1n S(X_1,\ldots,X_n)=S(X_1)
\]](entropie066.png)
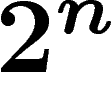 peut être codé par n unités
d'information. C'est le premier lien entre théorie de l'information et
codage.
peut être codé par n unités
d'information. C'est le premier lien entre théorie de l'information et
codage.
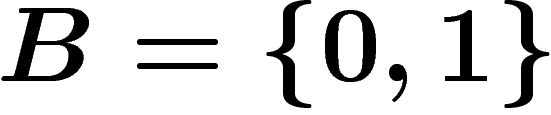 ). On dit que le codage est instantanément décodable
s'il n'existe pas deux lettres
). On dit que le codage est instantanément décodable
s'il n'existe pas deux lettres 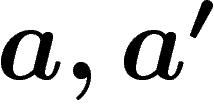 de A telles que le code de a
soit un préfixe du code de
de A telles que le code de a
soit un préfixe du code de 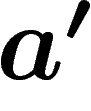 . Tous les codages ci-dessous seront
supposés instantanément décodables.
. Tous les codages ci-dessous seront
supposés instantanément décodables.
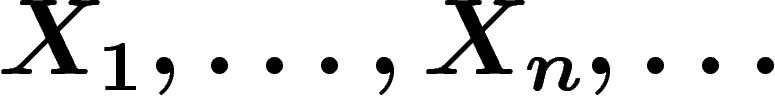 des variables aléatoires identiquement
distribuées à valeurs dans un ensemble A. Soit C un codage de A
utilisant un alphabet B. On définit la longueur moyenne du codage :
des variables aléatoires identiquement
distribuées à valeurs dans un ensemble A. Soit C un codage de A
utilisant un alphabet B. On définit la longueur moyenne du codage :
![\[
L(C)=\lim_n \frac1n \mathbb{E} \ell (C(X_1\ldots X_n))
\]](entropie072.png)
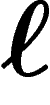 représente la longueur d'un mot sur l'alphabet B. On a alors
le théorème de codage de Shannon, qui identifie entropie et taux de
compression maximal :
représente la longueur d'un mot sur l'alphabet B. On a alors
le théorème de codage de Shannon, qui identifie entropie et taux de
compression maximal :
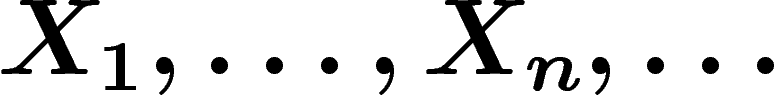 . Alors
. Alors
![\[
L(C)\geq \frac{S(X_1,\ldots,X_n,\ldots)}{\log \abs{B}}
\]](entropie075.png)
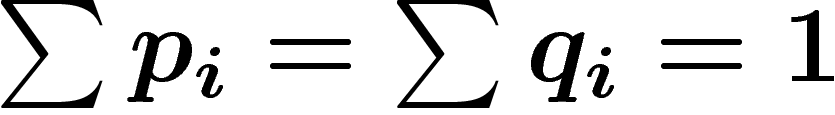 , alors
, alors 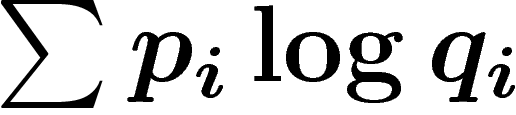 est maximal quand
est maximal quand 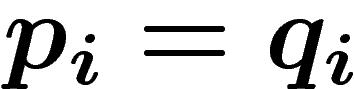 , et la
remarque que si les
, et la
remarque que si les 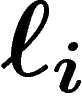 sont les longueurs des codes d'un codage
instantanément déchiffrable, on a
sont les longueurs des codes d'un codage
instantanément déchiffrable, on a 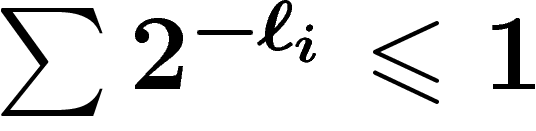 .
.
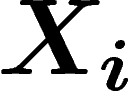 peuvent être
décomposés en deux classes, une classe de mots « typiques » et une
classe de mots « rares ». Les mots typiques sont environ au nombre de
peuvent être
décomposés en deux classes, une classe de mots « typiques » et une
classe de mots « rares ». Les mots typiques sont environ au nombre de
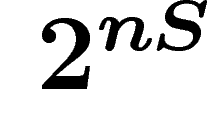 , chacun d'entre eux étant de probabilité environ
, chacun d'entre eux étant de probabilité environ 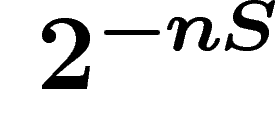 ; les
mots rares ont une probabilité totale négligeable. Pour coder dans
; les
mots rares ont une probabilité totale négligeable. Pour coder dans
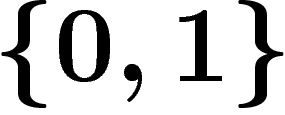 un mot typique, on met un « 0 » suivi du code en base
un mot typique, on met un « 0 » suivi du code en base  du
numéro du mot typique parmi les
du
numéro du mot typique parmi les 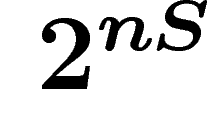 mots typiques (ce qui prend nS
chiffres en base
mots typiques (ce qui prend nS
chiffres en base  ) ; pour un mot rare, on met un « 1 » suivi
simplement du code en base
) ; pour un mot rare, on met un « 1 » suivi
simplement du code en base  du numéro du mot rare parmi l'ensemble des
mots possibles sur l'alphabet de départ.
du numéro du mot rare parmi l'ensemble des
mots possibles sur l'alphabet de départ.
 de longueur
de longueur 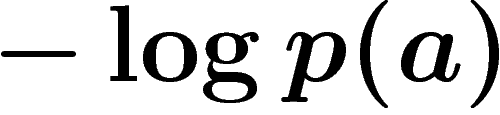 (arrondi à l'entier supérieur), ce qui est
toujours possible : par exemple, arranger les probabilités de manière
croissante sur l'intervalle
(arrondi à l'entier supérieur), ce qui est
toujours possible : par exemple, arranger les probabilités de manière
croissante sur l'intervalle ![$[0;1]$](entropie091.png) , ce qui donne une partition en
sous-intervalles, si un intervalle est de longueur
, ce qui donne une partition en
sous-intervalles, si un intervalle est de longueur 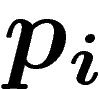 on peut trouver
un nombre binaire à
on peut trouver
un nombre binaire à 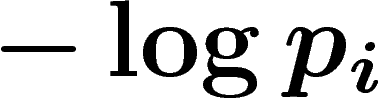 chiffres qu'on lui associe, de manière à
former un codage sans préfixes. Autrement dit on code les lettres plus
fréquentes par des mots plus courts.
chiffres qu'on lui associe, de manière à
former un codage sans préfixes. Autrement dit on code les lettres plus
fréquentes par des mots plus courts.
 une fonction de
décodage, on veut que
une fonction de
décodage, on veut que 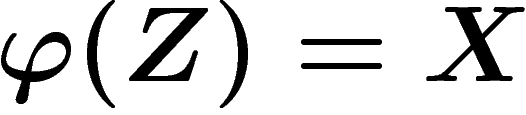 le plus souvent possible, mais le
passage de X vers Z n'est pas forcément injectif. Le théorème
suivant, dû à Fano, affirme que la probabilité minimale d'erreur est liée
à l'entropie :
le plus souvent possible, mais le
passage de X vers Z n'est pas forcément injectif. Le théorème
suivant, dû à Fano, affirme que la probabilité minimale d'erreur est liée
à l'entropie :
 , la probabilité que
, la probabilité que 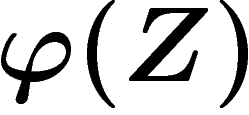 soit
différent de X est supérieure ou égale à
soit
différent de X est supérieure ou égale à ![\[
\frac{S(X|Z)-1}{\log\abs{X}}
\]](entropie098.png)
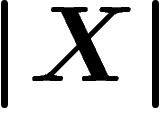 est la taille de l'alphabet de X.
est la taille de l'alphabet de X.
 . Auparavant, il code X par une
suite binaire Y de longueur
. Auparavant, il code X par une
suite binaire Y de longueur 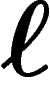 . Le récepteur, lui, reçoit à la
sortie du canal une suite binaire Z qui est une fonction aléatoire
de la suite binaire Y donnée à l'entrée du canal.
. Le récepteur, lui, reçoit à la
sortie du canal une suite binaire Z qui est une fonction aléatoire
de la suite binaire Y donnée à l'entrée du canal.
 par
par
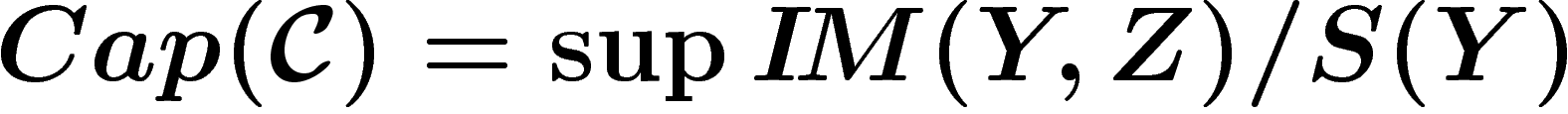 , le sup étant pris sur toutes les
lois de probabilité possibles pour le mot binaire Y. Cette quantité ne
dépend que du canal.
, le sup étant pris sur toutes les
lois de probabilité possibles pour le mot binaire Y. Cette quantité ne
dépend que du canal.
 et des
et des  , mais,
avec une faible probabilité p, change un
, mais,
avec une faible probabilité p, change un  en
en  ou un
ou un  en
en  .
La capacité est alors
.
La capacité est alors 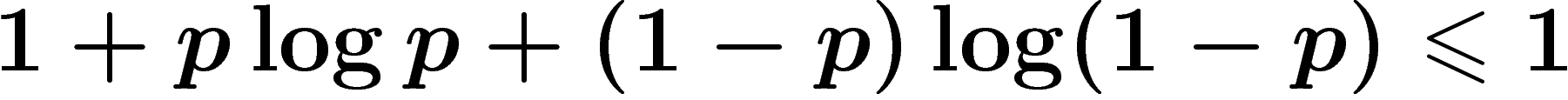 . Dans le cas où
. Dans le cas où
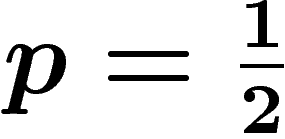 , aucune information ne peut être tirée, la capacité est
nulle.
, aucune information ne peut être tirée, la capacité est
nulle.
 pour une certaine longueur
pour une certaine longueur 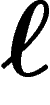 (pour
simplifier, on considère des codages à longueur constante). On définit
la probabilité d'erreur
(pour
simplifier, on considère des codages à longueur constante). On définit
la probabilité d'erreur 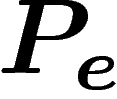 d'un codage C (avec fonction de décodage
D) par
d'un codage C (avec fonction de décodage
D) par 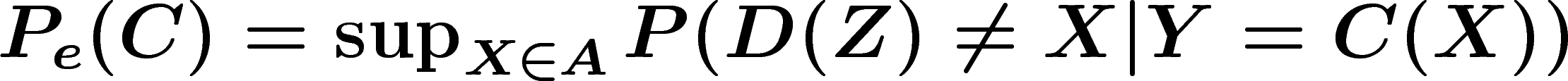 . On définit aussi le
taux de compression du codage par
. On définit aussi le
taux de compression du codage par 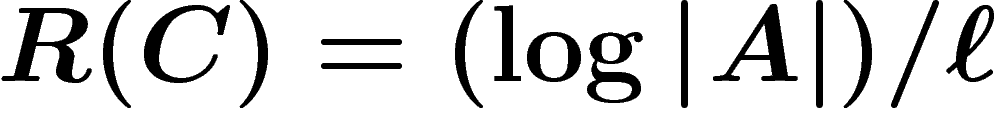 .
.
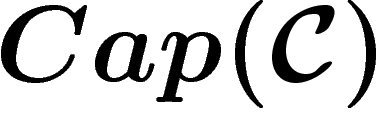 d'un canal
d'un canal  est
égale au sup des nombres R tels que, pour tout
est
égale au sup des nombres R tels que, pour tout 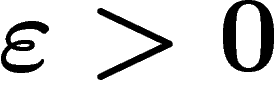 , il existe un
alphabet A, une longueur
, il existe un
alphabet A, une longueur 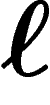 , un codage
, un codage  tels que
tels que 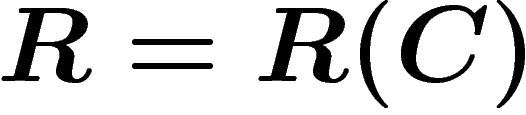 et
et 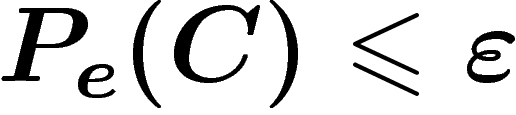 .
.
 . Par analogie avec le cas discret,
l'entropie d'une distribution de probabilité f sur
. Par analogie avec le cas discret,
l'entropie d'une distribution de probabilité f sur 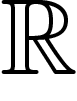 est égale à
est égale à
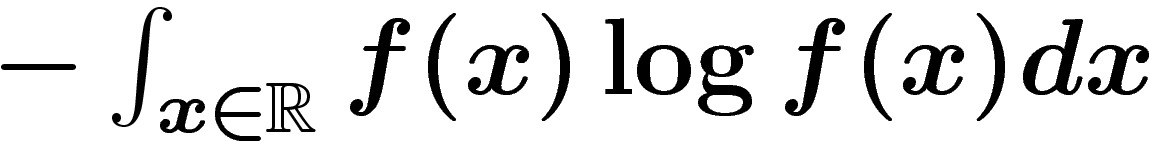 .
.
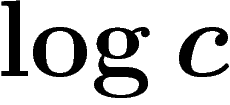 à l'entropie de l'information transmise (ce qui
est naturel : en multipliant par
à l'entropie de l'information transmise (ce qui
est naturel : en multipliant par  on a une précision deux fois plus
grande, ce qui donne un bit d'information en plus). Pour
obtenir des résultats pertinents, on suppose en général que les canaux
utilisés sont limités en puissance, par exemple qu'ils ne peuvent pas
transmettre une variable dont la variance est supérieure à un certain
seuil (sans cette hypothèse, on peut facilement transmettre une quantité
infinie d'information).
on a une précision deux fois plus
grande, ce qui donne un bit d'information en plus). Pour
obtenir des résultats pertinents, on suppose en général que les canaux
utilisés sont limités en puissance, par exemple qu'ils ne peuvent pas
transmettre une variable dont la variance est supérieure à un certain
seuil (sans cette hypothèse, on peut facilement transmettre une quantité
infinie d'information).
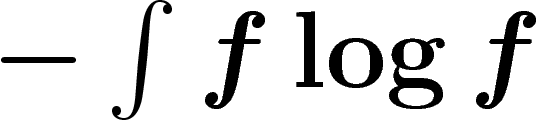 , et
calculons l'entropie d'une fonction voisine
, et
calculons l'entropie d'une fonction voisine 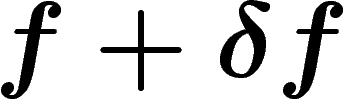 de même
variance. Comme
de même
variance. Comme 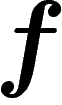 et
et 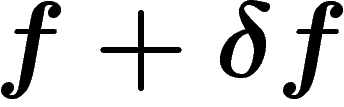 sont des mesures de probabilité,
donc d'intégrale
sont des mesures de probabilité,
donc d'intégrale  , on a
, on a 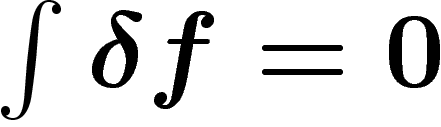 . On peut supposer que f et
. On peut supposer que f et
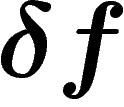 sont de moyenne nulle (par translation), et donc
sont de moyenne nulle (par translation), et donc 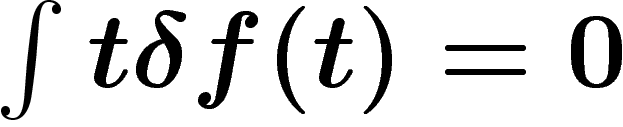 . Alors le fait que
. Alors le fait que 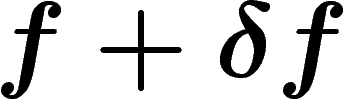 ait même variance que f
s'écrit
ait même variance que f
s'écrit 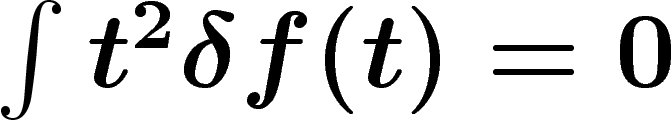 . Maintenant, la variation d'entropie est
. Maintenant, la variation d'entropie est
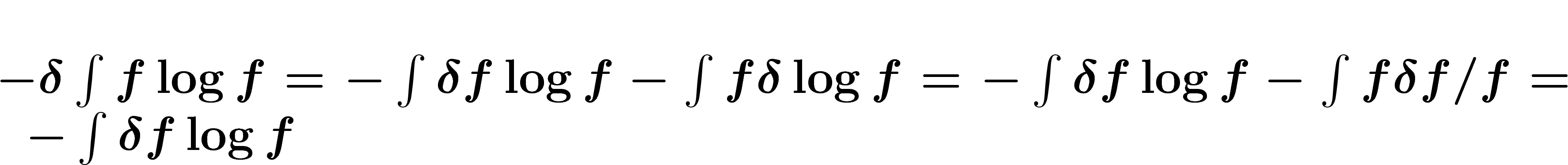 . Pour tout
. Pour tout
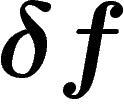 vérifiant
vérifiant 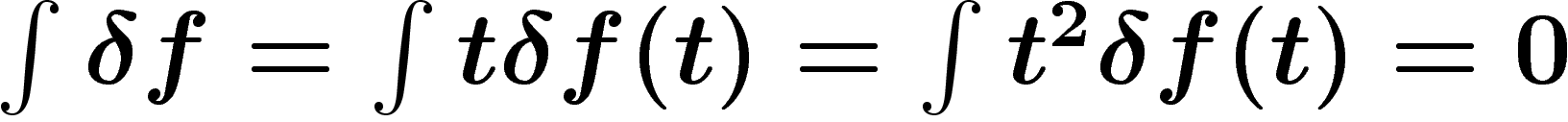 , on doit donc avoir
, on doit donc avoir 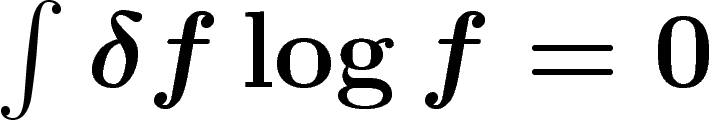 si f est un
extrémum d'entropie. Cela implique
si f est un
extrémum d'entropie. Cela implique 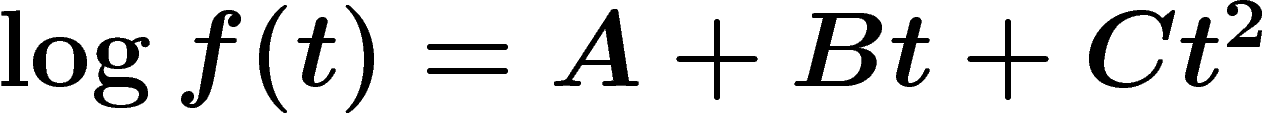 , d'où la
gaussienne.
, d'où la
gaussienne.
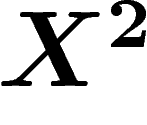 doit être inférieure à p). Mais ce canal est
bruité ; plus exactement, on a un ennemi qui a accès à ce canal et qui
peut transmettre du bruit Y (indépendant de X), la puissance du bruit
transmis étant inférieure à
doit être inférieure à p). Mais ce canal est
bruité ; plus exactement, on a un ennemi qui a accès à ce canal et qui
peut transmettre du bruit Y (indépendant de X), la puissance du bruit
transmis étant inférieure à 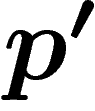 . Le récepteur reçoit
. Le récepteur reçoit 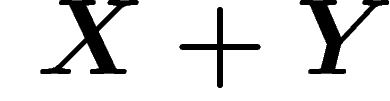 , qui fait
perdre de l'information par rapport à X. Ce qui intéresse le
transmetteur est de maximiser
, qui fait
perdre de l'information par rapport à X. Ce qui intéresse le
transmetteur est de maximiser 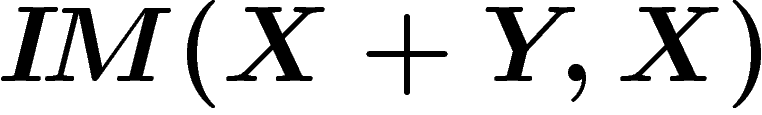 à Y donné, tandis que
l'ennemi cherche à minimiser cette quantité à X donné (si chacun
connaît la stratégie appliquée par l'autre).
à Y donné, tandis que
l'ennemi cherche à minimiser cette quantité à X donné (si chacun
connaît la stratégie appliquée par l'autre).
![\[
\inf_Y\sup_X I\!M(X+Y,X)=\sup_X\inf_Y I\!M(X+Y,X)=\frac12\log(1+\frac{p}{p'})
\]](entropie148.png)
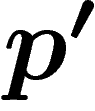 .
.
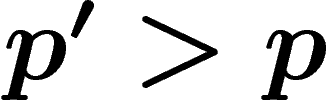 , il reste encore quelque chose du message
initial.
, il reste encore quelque chose du message
initial.
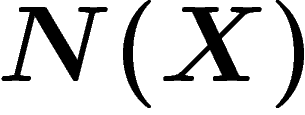 d'une variable X comme la variance qu'aurait
une gaussienne de même entropie que X. (On vérifie qu'en dimension d,
on a
d'une variable X comme la variance qu'aurait
une gaussienne de même entropie que X. (On vérifie qu'en dimension d,
on a 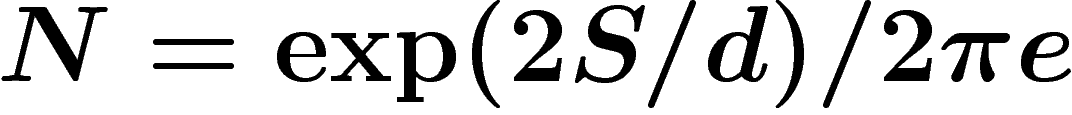 .)
.)
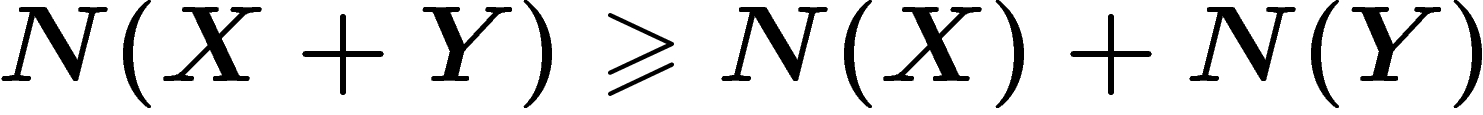 .
Pour conserver l'information on doit monter en puissance... Autre forme
équivalente :
pour
.
Pour conserver l'information on doit monter en puissance... Autre forme
équivalente :
pour 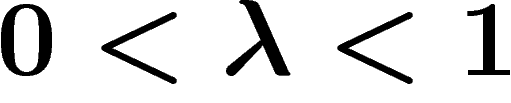 , si X et Y sont des
variables aléatoires indépendantes, alors
, si X et Y sont des
variables aléatoires indépendantes, alors
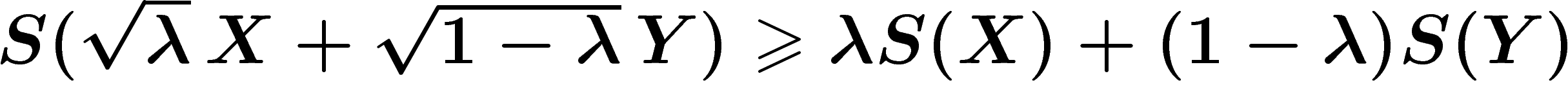 . Ceci peut servir à montrer par exemple que si
. Ceci peut servir à montrer par exemple que si
 sont des variables aléatoires indépendantes
identiquement distribuées, alors
sont des variables aléatoires indépendantes
identiquement distribuées, alors  ressemble à
une gaussienne (au moins si n est une puissance de
ressemble à
une gaussienne (au moins si n est une puissance de  )...
)...
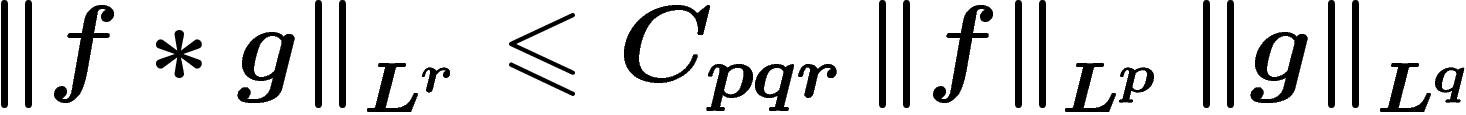 pour
pour 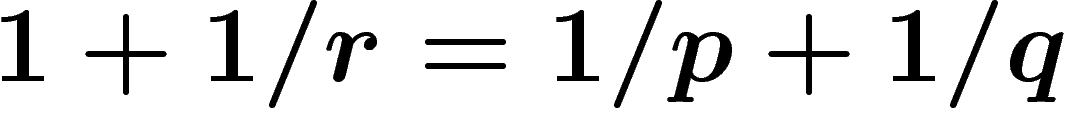 ...
...