![\[
S(E)=k \log \mathrm{vol} \{(p,q),\,E\leq E(p,q)\leq E+\delta E\}
\]](entropie340.png)
En physique, l'entropie d'un système hamiltonien à l'énergie E est définie comme le log du volume de l'espace des phases qui est à l'énergie E :
![\[
S(E)=k \log \mathrm{vol} \{(p,q),\,E\leq E(p,q)\leq E+\delta E\}
\]](entropie340.png)
On veut définir un analogue en théorie des probabilités. L'idée est que,
comme en physique statistique, on va regarder une variable 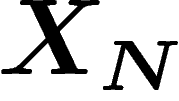 dépendant d'un grand nombre N d'événements élémentaires. La constante
de Boltzmann ci-dessus, k, est égale à la constante des gaz parfaits
divisée par le nombre de particules impliquées (le nombre d'Avogadro), on
est donc tenté de remplacer cette constante par
dépendant d'un grand nombre N d'événements élémentaires. La constante
de Boltzmann ci-dessus, k, est égale à la constante des gaz parfaits
divisée par le nombre de particules impliquées (le nombre d'Avogadro), on
est donc tenté de remplacer cette constante par 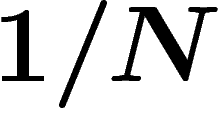 . Le volume
s'interprète tout naturellement en terme de probabilité, et on pose :
. Le volume
s'interprète tout naturellement en terme de probabilité, et on pose :
![\[
H(E)=-\frac1N \log \P(E\leq X_N\leq E+\delta E)
\]](entropie343.png)
 parce qu'une probabilité est inférieure à
parce qu'une probabilité est inférieure à  .
.
L'idée est qu'on arrive souvent à évaluer l'entropie d'un événement au
moyen de la théorie de l'information. Cela fournit alors directement une
évaluation de la probabilité d'un événement : presque par définition, un
événement apportant une quantité d'information H a une probabilité
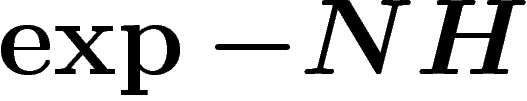 .
.
On commence par donner l'exemple le plus simple d'une telle situation, avant d'expliquer en termes d'entropie les théorèmes plus généraux.
On considère un alphabet fini à n lettres 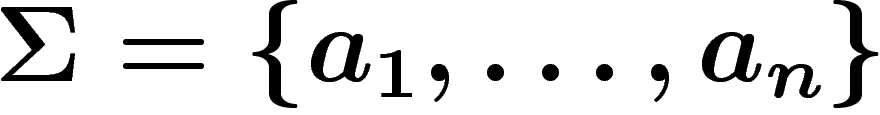 .
On se donne une loi de probabilité
.
On se donne une loi de probabilité 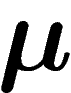 sur cet alphabet et on tire, de
manière indépendante, une suite de lettres
sur cet alphabet et on tire, de
manière indépendante, une suite de lettres  selon cette loi. La proportion de
selon cette loi. La proportion de 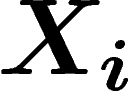 qui sont égales à une lettre
qui sont égales à une lettre
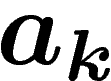 est, d'après la loi des grands nombres,
est, d'après la loi des grands nombres, 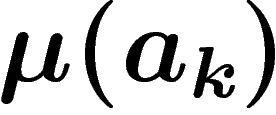 . Ce qui nous
intéresse est le comportement asymptotique de la probabilité que, sur les
N premières lettres, cette proportion ait une valeur très différente,
mettons
. Ce qui nous
intéresse est le comportement asymptotique de la probabilité que, sur les
N premières lettres, cette proportion ait une valeur très différente,
mettons 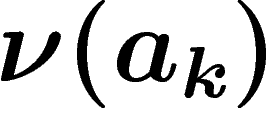 . Autrement dit : quelle est la probabilité qu'un dé
non pipé sorte des « six » un quart du temps ? (Ou : si un dé prétendu
non pipé sort des « six » un quart du temps, que doit-on conclure ?)
. Autrement dit : quelle est la probabilité qu'un dé
non pipé sorte des « six » un quart du temps ? (Ou : si un dé prétendu
non pipé sort des « six » un quart du temps, que doit-on conclure ?)
On définit donc la mesure empirique des 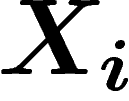 par
par
![\[
L_N(a_k)=\frac1N \#\{i\leq N, X_i=a_k\}
\]](entropie355.png)
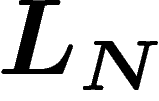 est une variable aléatoire dont la valeur est une mesure de probabilité
sur
est une variable aléatoire dont la valeur est une mesure de probabilité
sur 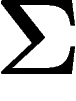 .
(À noter que n'importe quelle mesure sur
.
(À noter que n'importe quelle mesure sur 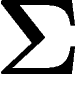 ne peut pas être une
mesure empirique : les fréquences doivent être des multiples de
ne peut pas être une
mesure empirique : les fréquences doivent être des multiples de 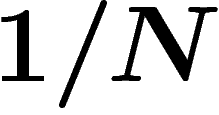 .)
.)
Ce qui nous intéresse est d'évaluer la probabilité que 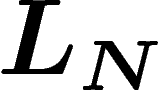 soit proche d'une
certaine mesure
soit proche d'une
certaine mesure 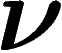 sur
sur  . Pour cela, on va évaluer la quantité
d'information H fournie par l'événement « la mesure empirique est
. Pour cela, on va évaluer la quantité
d'information H fournie par l'événement « la mesure empirique est
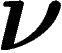 », et la réponse sera alors : la probabilité est
», et la réponse sera alors : la probabilité est 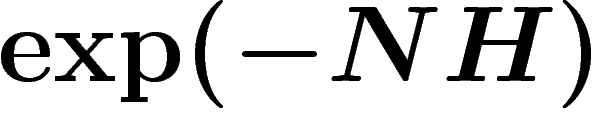 .
.
On rappelle qu'en théorie de l'information, l'occurrence d'un événement
x qui était de probabilité 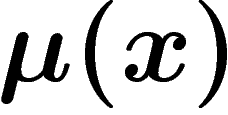 apporte une information
apporte une information
![\[
I_\mu(x)=-\log \mu(x)
\]](entropie366.png)
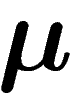 est l'espérance de la
quantité d'information obtenue en tirant un élément selon
est l'espérance de la
quantité d'information obtenue en tirant un élément selon 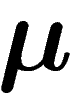 :
:
![\[
H(\mu)=\E_\mu I_\mu =-\sum \mu_i\log \mu_i
\]](entropie369.png)
Spécifier un élément d'un ensemble, sachant que cet élément allait être
tiré selon la loi 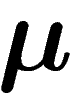 , apporte donc en moyenne une information
, apporte donc en moyenne une information
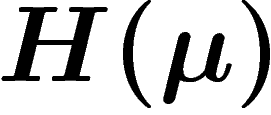 .
.
Maintenant, on peut se demander quelle information (par rapport à 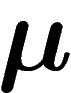 )
est apportée par l'affirmation suivante : « en fait, l'élément va être
tiré selon une autre loi
)
est apportée par l'affirmation suivante : « en fait, l'élément va être
tiré selon une autre loi 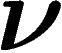 ». Cela apporte assurément une
information : par exemple, si
». Cela apporte assurément une
information : par exemple, si 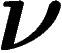 est concentrée en un point x, cela
revient à donner directement x ce qui apporte une information
est concentrée en un point x, cela
revient à donner directement x ce qui apporte une information
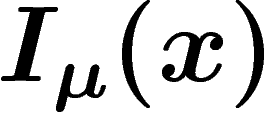 . On définit l'information relative :
. On définit l'information relative :
![\[
I_{\nu|\mu}(x)=I_\mu(x)-I_\nu(x)
\]](entropie376.png)
![\[
H(\nu|\mu)=\E_\nu I_{\nu|\mu}=\sum \nu(x)\log \frac{\nu(x)}{\mu(x)}=\sum
\frac{\nu(x)}{\mu(x)}\log \frac{\nu(x)}{\mu(x)}\,\, \mu(x)
\]](entropie377.png)
On montre que 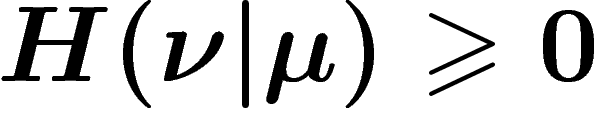 , d'où le choix des signes (c'est
essentiellement la convexité de
, d'où le choix des signes (c'est
essentiellement la convexité de 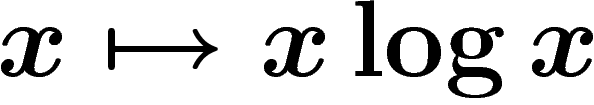 ).
).
L'interprétation est la suivante : si on tire un élément sous la loi
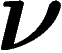 , l'information moyenne qui sera au final obtenue sera
, l'information moyenne qui sera au final obtenue sera 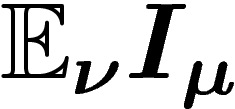 , par rapport à
, par rapport à 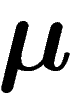 . Or effectuer un tirage selon une loi
. Or effectuer un tirage selon une loi 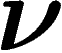 ne fait apparaître, dans l'absolu, qu'une information
ne fait apparaître, dans l'absolu, qu'une information 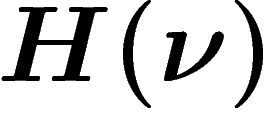 . C'est
donc qu'en sachant que l'élément allait être tiré selon
. C'est
donc qu'en sachant que l'élément allait être tiré selon 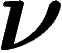 , on
possédait dès le départ une information
, on
possédait dès le départ une information 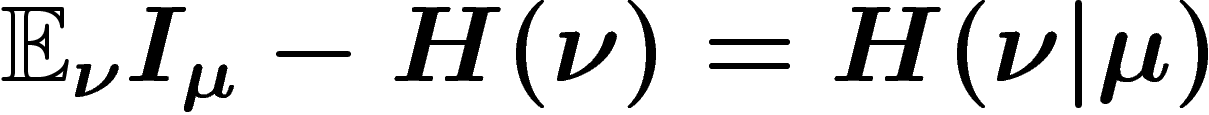 , par
rapport à la loi
, par
rapport à la loi 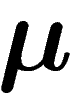 .
.
Moralement, cette quantité d'information peut servir à définir une distance sur l'espace des mesures de probabilité sur un ensemble (mais elle n'est pas symétrique).
Revenons à la loi de la mesure empirique 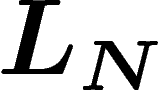 de variables aléatoires
de variables aléatoires
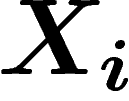 tirées dans
tirées dans 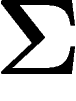 selon la loi
selon la loi 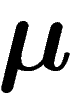 . Un raisonnement intuitif,
à ce point, permettrait d'obtenir le résultat. En effet, si la loi
empirique est
. Un raisonnement intuitif,
à ce point, permettrait d'obtenir le résultat. En effet, si la loi
empirique est 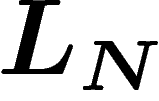 , c'est comme si on avait tiré N fois de suite les
, c'est comme si on avait tiré N fois de suite les
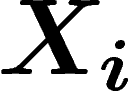 selon la loi
selon la loi 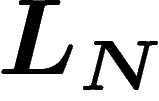 . Ceci apporte une information
. Ceci apporte une information 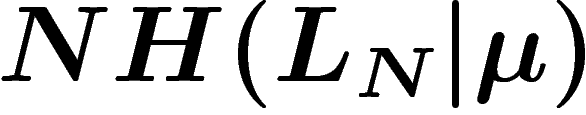 . Un
événement d'information H ayant probabilité
. Un
événement d'information H ayant probabilité 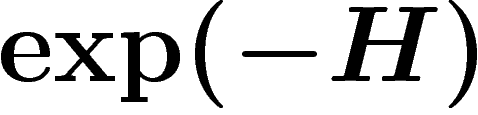 , on en conclut
que la probabilité que la mesure empirique
, on en conclut
que la probabilité que la mesure empirique 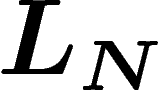 soit égale à une
certaine loi
soit égale à une
certaine loi 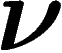 se comporte comme
se comporte comme 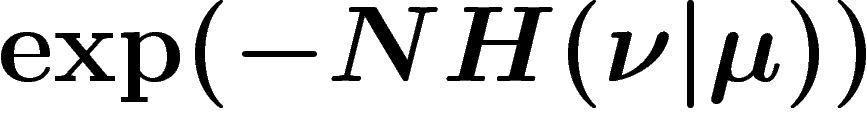 .
.
Cela se passe presque ainsi. Soit donc 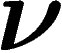 une loi sur
une loi sur  . Soit
. Soit
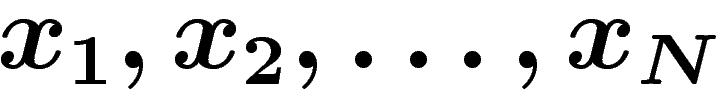 une suite de lettres de
une suite de lettres de 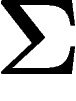 , telle que la
proportion de
, telle que la
proportion de 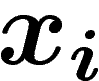 égaux à une lettre
égaux à une lettre 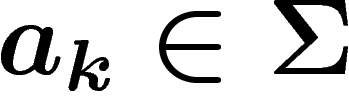 soit
soit 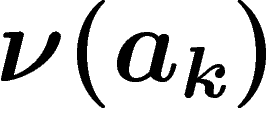 .
Calculons la probabilité (sous
.
Calculons la probabilité (sous 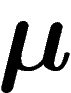 ) que
) que
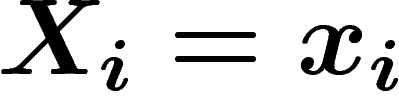 . Cette probabilité est
. Cette probabilité est 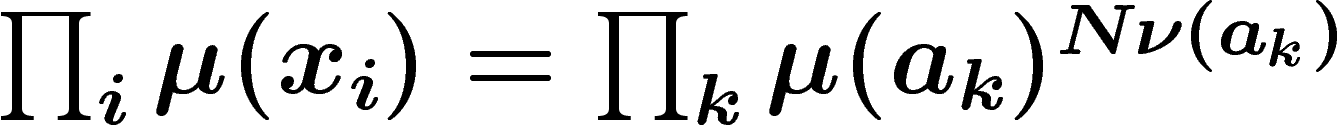 , et ou encore
, et ou encore 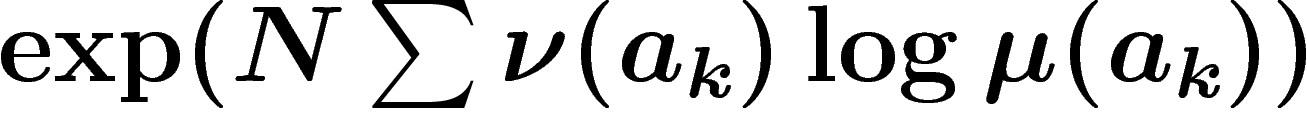 , soit encore
, soit encore
![\[
\P_\mu(x_1,x_2,\ldots,x_N)=\exp \,-N(H(\nu)+H(\nu|\mu))
\]](entropie411.png)
Pour évaluer la probabilité que la fréquence empirique soit 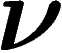 , il
reste donc à multiplier cette quantité par le nombre de suites
, il
reste donc à multiplier cette quantité par le nombre de suites
 telles que la proportion des
telles que la proportion des 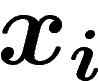 égaux à la letrte
égaux à la letrte
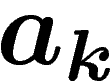 soit
soit 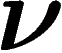 . Pour cela, on suppose bien sûr que
. Pour cela, on suppose bien sûr que 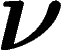 est réalisable
comme une telle fréquence, i.e. que les valeurs de
est réalisable
comme une telle fréquence, i.e. que les valeurs de 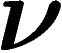 sont multiples
de
sont multiples
de 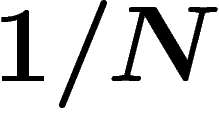 .
.
Ce nombre vaut 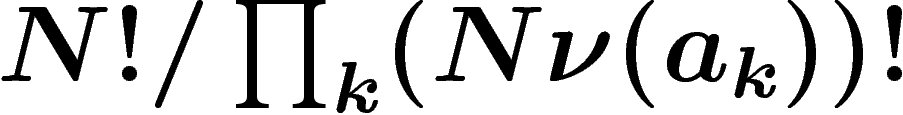 , qui, par un calcul très simple
(essentiellement, celui de Boltzmann), vaut environ
, qui, par un calcul très simple
(essentiellement, celui de Boltzmann), vaut environ 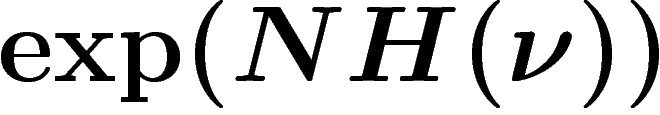 quand
N est grand (à un facteur polynomial en N près), ce qui est bien
naturel quand on sait que spécifier une suite particulière parmi
l'ensemble des suites de fréquence empirique
quand
N est grand (à un facteur polynomial en N près), ce qui est bien
naturel quand on sait que spécifier une suite particulière parmi
l'ensemble des suites de fréquence empirique 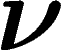 , fournit une
information
, fournit une
information  .
.
Conclusion : si 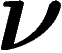 est réalisable comme fréquence d'une suite à N
termes, alors la probabilité, sous
est réalisable comme fréquence d'une suite à N
termes, alors la probabilité, sous 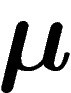 , que la fréquence empirique
, que la fréquence empirique
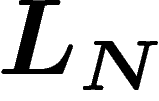 soit égale à
soit égale à 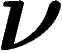 est donc environ
est donc environ
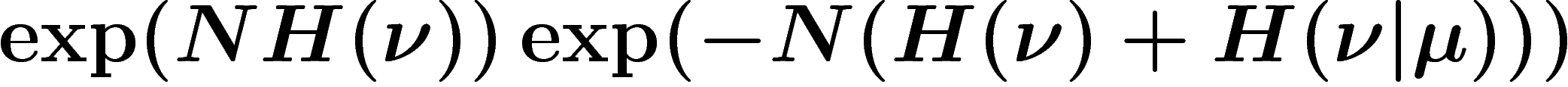 , soit
, soit
![\[
\P_\mu(L_N=\nu)\approx \exp(-NH(\nu|\mu))
\]](entropie429.png)
Pour se débarrasser des problèmes de lois réalisables ou non, on va
plutôt calculer la probabilité que 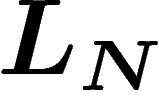 tombe dans un petit ensemble
autour de
tombe dans un petit ensemble
autour de 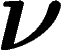 . On énonce alors le théorème de Sanov :
. On énonce alors le théorème de Sanov :
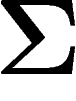 , et soit
, et soit 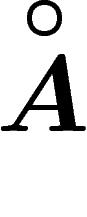 son intérieur. La
probabilité que la mesure empirique
son intérieur. La
probabilité que la mesure empirique 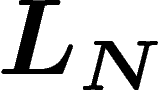 d'une suite de variables
indépendantes tirées dans
d'une suite de variables
indépendantes tirées dans 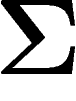 avec la loi
avec la loi 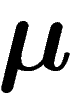 , appartienne à A,
vérifie :
, appartienne à A,
vérifie :
![\[
-\inf_{\nu\in \overset{\circ}A}H(\nu|\mu)\leq
\vliminf_{N\rightarrow \infty}\frac 1N \log\P_\mu(L_N\in A)
\leq \vlimsup_{N\rightarrow \infty}\frac 1N \log\P_\mu(L_N\in A)
\leq -\inf_{\nu\in A} H(\nu|\mu)
\]](entropie437.png)
Autrement dit, c'est la mesure la plus « proche » de 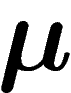 au sens de la
distance
au sens de la
distance 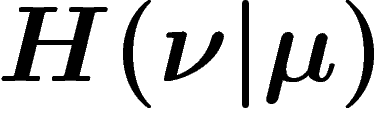 qui contrôle le taux de décroissance de cette
probabilité.
qui contrôle le taux de décroissance de cette
probabilité.
Le principe des grandes déviations est une généralisation de la situation
précédente. En particulier, on ne demande plus forcément l'indépendance.
On considère donc une suite de mesures de probabilité 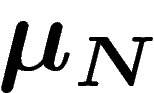 sur un
espace X régulier (par exemple, métrisable avec sa tribu borélienne). On
comprend que la mesure
sur un
espace X régulier (par exemple, métrisable avec sa tribu borélienne). On
comprend que la mesure 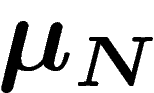 dépend de N « événements de base ».
L'information ne croît pas forcément linéairement en N, on considère
donc une suite de nombres
dépend de N « événements de base ».
L'information ne croît pas forcément linéairement en N, on considère
donc une suite de nombres 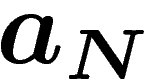 qui jauge cette croissance.
qui jauge cette croissance.
On considère une fonction ![$I:X\rightarrow[0;\infty]$](entropie443.png) candidate à être la
fonction entropie des
candidate à être la
fonction entropie des 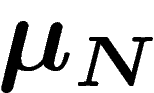 . On suppose en général que I est semi-continue
inférieurement (c'est-à-dire que les
. On suppose en général que I est semi-continue
inférieurement (c'est-à-dire que les ![$I^{-1}([0;A])$](entropie445.png) sont fermés), et on
qualifie cette fonction de « bonne fonction de taux » si les
sont fermés), et on
qualifie cette fonction de « bonne fonction de taux » si les
![$I^{-1}([0;A])$](entropie446.png) sont compacts.
sont compacts.
On dit alors que la famille 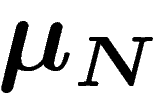 satisfait le principe des grandes
déviations pour la bonne fonction de taux I, si
pour tout fermé
satisfait le principe des grandes
déviations pour la bonne fonction de taux I, si
pour tout fermé  , on a
, on a
![\[
\vlimsup_{N\rightarrow\infty}\frac1{a_N}\log \mu_N(F)\leq -\inf_F I
\]](entropie449.png)
 , on a
, on a
![\[
\vliminf_{N\rightarrow\infty}\frac1{a_N}\log \mu_N(\mathcal{O})\geq -\inf_{\mathcal{O}}I
\]](entropie451.png)
Le principe de grandes déviations est donc analogue à l'existence d'une entropie.
Si on a des variables satisfaisant un principe de grandes déviations, et
que la fonction d'entropie I admet un minimum (qui vaut alors forcément
 , la probabilité totale étant
, la probabilité totale étant  ) et est régulière, il est tentant de
développer I à l'ordre
) et est régulière, il est tentant de
développer I à l'ordre  au voisinage de ce minimum, pour trouver que
la renormalisation en
au voisinage de ce minimum, pour trouver que
la renormalisation en 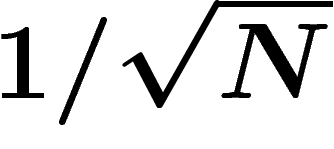 plutôt qu'en
plutôt qu'en 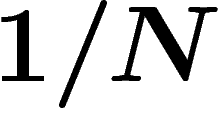 , autour de la
moyenne, donne une gaussienne... Bien sûr, on aurait aussi pu développer
la probabilité à l'ordre
, autour de la
moyenne, donne une gaussienne... Bien sûr, on aurait aussi pu développer
la probabilité à l'ordre  au voisinage de son maximum, on aurait
trouvé que localement la probabilité se comportait comme une parabole
osculant la gaussienne ci-dessus à l'ordre
au voisinage de son maximum, on aurait
trouvé que localement la probabilité se comportait comme une parabole
osculant la gaussienne ci-dessus à l'ordre  . Pour que la probabilité
ressemble vraiment à une gaussienne, il faut donc vérifier que le
développement de I est valable (par exemple, il suffit que la dérivée
troisième soit contrôlée).
. Pour que la probabilité
ressemble vraiment à une gaussienne, il faut donc vérifier que le
développement de I est valable (par exemple, il suffit que la dérivée
troisième soit contrôlée).
Alors, si I a un unique minimum au point
z, on peut vérifier que 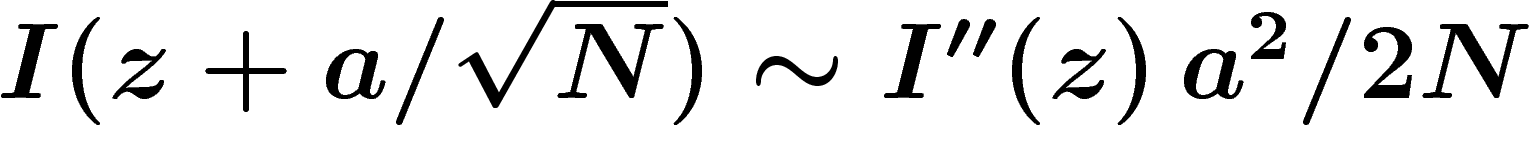 et que
la probabilité correspondante est donc
et que
la probabilité correspondante est donc 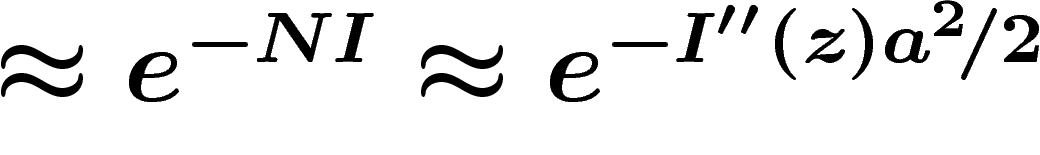 ,
autrement dit qu'on a une gaussienne de variance
,
autrement dit qu'on a une gaussienne de variance 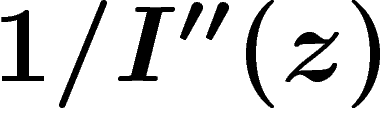 .
.
On avait vu en théorie de l'information que les gaussiennes maximisaient l'entropie à variance donnée, c'est exactement le phénomène qu'on retrouve ici : notre estimation de probabilités provient d'une maximisation d'entropie, et on renormalise à l'ordre deux au voisinage du maximum. Une fois de plus, les gaussiennes trouvent leur origine dans une quantité d'information...
À ce stade, on peut donner une première généralisation : plutôt que de
s'intéresser à la mesure empirique des 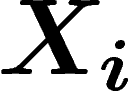 , on peut considérer une
fonction quelconque
, on peut considérer une
fonction quelconque 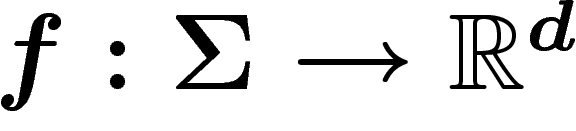 , et s'intéresser à sa
moyenne empirique
, et s'intéresser à sa
moyenne empirique 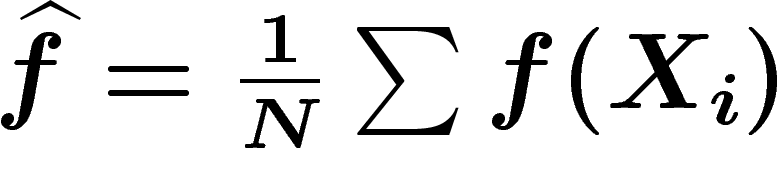 . Si on prend
. Si on prend
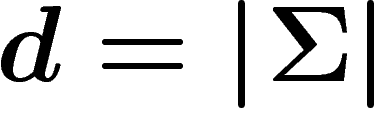 et qu'on prend
et qu'on prend 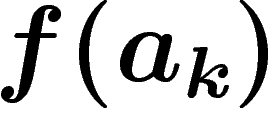 égal au k-ième vecteur d'une
base de
égal au k-ième vecteur d'une
base de 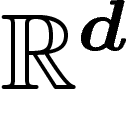 , on retrouve bien évidemment le cas précédent.
, on retrouve bien évidemment le cas précédent.
Si 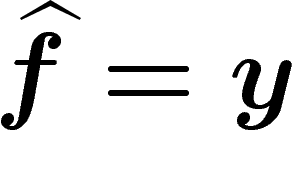 , cela signifie que la fréquence empirique
, cela signifie que la fréquence empirique 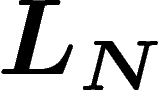 des
des
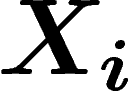 vérifie
vérifie 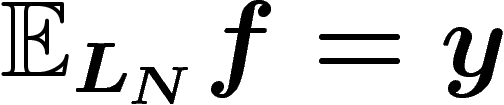 , par définition. On est donc tenté de dire
que la probabilité que
, par définition. On est donc tenté de dire
que la probabilité que 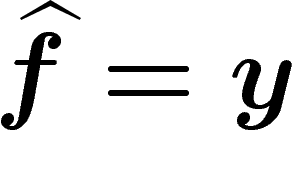 est la somme, pour toutes les
mesures
est la somme, pour toutes les
mesures 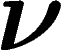 sur
sur 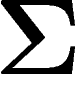 satisfaisant
satisfaisant 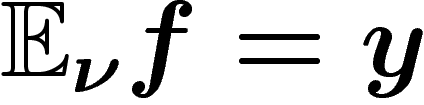 , de la probabilité
que
, de la probabilité
que 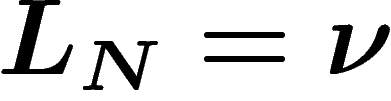 . Cette probabilité, comme ci-dessus, est
asymptotiquement
. Cette probabilité, comme ci-dessus, est
asymptotiquement 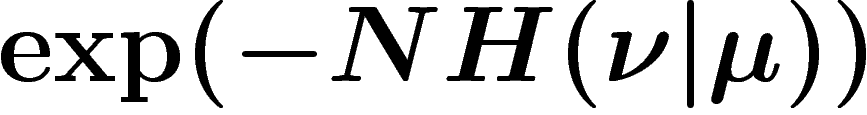 .
.
Quand N est grand, seule la contribution du meilleur 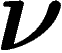 (c'est-à-dire celui minimisant la « distance »
(c'est-à-dire celui minimisant la « distance » 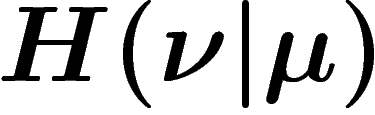 ) compte, les
autres devenant négligeables. Posons donc, pour
) compte, les
autres devenant négligeables. Posons donc, pour 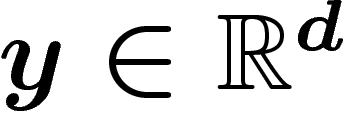 :
:
![\[
I(y)=\inf \{H(\nu|\mu), \nu\text{ mesure de probabilité sur }\Sigma\text{ telle que }\E_\nu f=y\}
\]](entropie481.png)
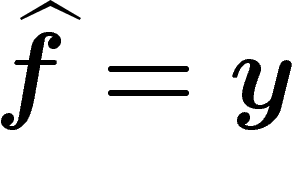 . On peut alors énoncer le théorème suivant :
. On peut alors énoncer le théorème suivant :
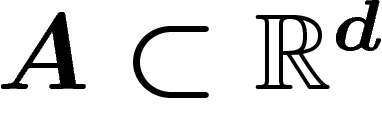 , d'intérieur
, d'intérieur 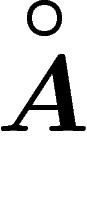 . La probabilité que
la moyenne empirique
. La probabilité que
la moyenne empirique 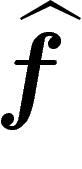 tombe dans A vérifie
tombe dans A vérifie
![\[
-\inf_{\overset{\circ}A}I\leq
\vliminf_{N\rightarrow\infty} \frac 1N \log \P_\mu(\widehat{f}\in A)
\leq
\vlimsup_{N\rightarrow\infty} \frac 1N \log \P_\mu(\widehat{f}\in A)
\leq
-\inf_{A} I
\]](entropie486.png)
On va désormais illustrer ce principe dans un cas un peu plus général que
le théorème de Sanov. Soient 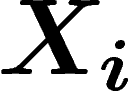 des variables aléatoires à valeurs
dans
des variables aléatoires à valeurs
dans 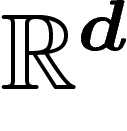 , éventuellement non indépendantes, ni identiquement
distribuées. On considère la moyenne empirique
, éventuellement non indépendantes, ni identiquement
distribuées. On considère la moyenne empirique 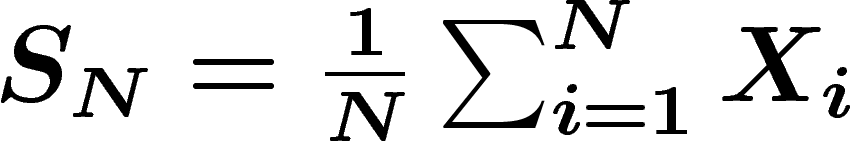 . Soit
. Soit 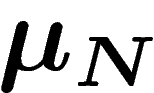 la loi de
la loi de 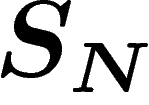 . On va montrer que sous certaines
hypothèses,
. On va montrer que sous certaines
hypothèses, 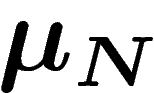 satisfait un principe de grandes déviations, pour une
fonction de taux à déterminer.
satisfait un principe de grandes déviations, pour une
fonction de taux à déterminer.
Comme précédemment, on a envie de dire que si 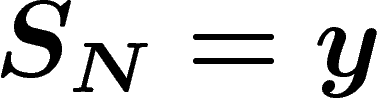 , cela signifie
qu'en fait, les
, cela signifie
qu'en fait, les 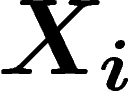 ont collectivement une distribution empirique
ont collectivement une distribution empirique 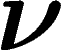 qui est de moyenne y, i.e.
qui est de moyenne y, i.e. 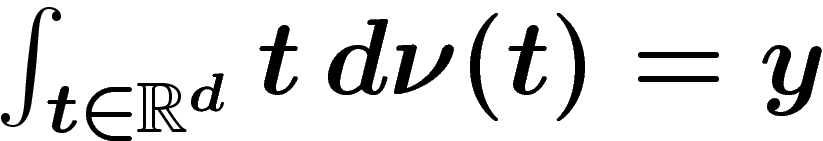 .
.
On voudrait alors dire que la probabilité d'une telle situation est
 , ou plutôt
, ou plutôt 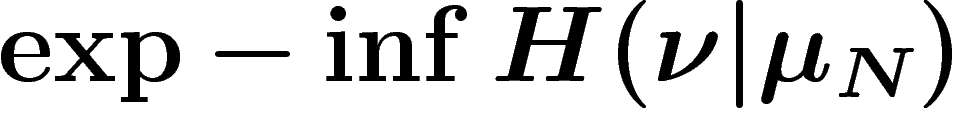 , l'inf étant
pris sur toutes les mesures
, l'inf étant
pris sur toutes les mesures 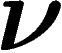 satisfaisant la contrainte d'être de
moyenne y : asymptotiquement, les contributions des mesures ne
réalisant pas l'inf sont négligeables.
satisfaisant la contrainte d'être de
moyenne y : asymptotiquement, les contributions des mesures ne
réalisant pas l'inf sont négligeables.
Comme les 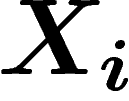 ne sont pas indépendantes, on va plutôt travailler avec
la loi jointe
ne sont pas indépendantes, on va plutôt travailler avec
la loi jointe 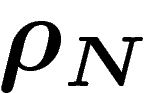 du N-uplet
du N-uplet 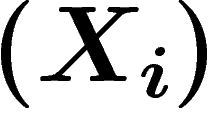 dans
dans 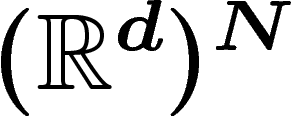 . On
cherche maintenant des lois
. On
cherche maintenant des lois 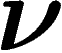 sur
sur 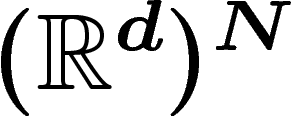 soumises à la contrainte
que
soumises à la contrainte
que 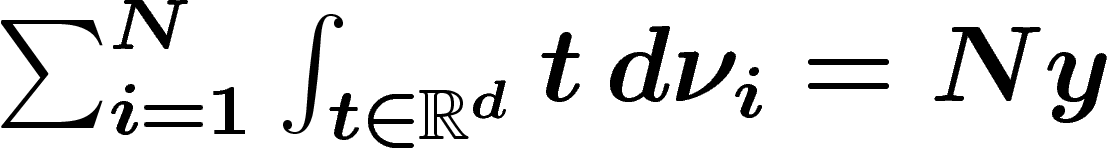 , où
, où 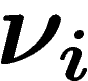 est la
loi de la i-ième composante de
est la
loi de la i-ième composante de 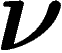 : la somme des moyennes sur chaque
composante doit être égale à Ny. Parmi celles-ci on cherche celle qui a
l'entropie minimale par rapport à la mesure
: la somme des moyennes sur chaque
composante doit être égale à Ny. Parmi celles-ci on cherche celle qui a
l'entropie minimale par rapport à la mesure 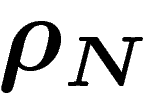 .
.
Ici intervient la remarque fondamentale suivante : à moyenne fixée,
les distributions qui minimisent l'entropie sont les distributions
exponentielles (ou maxwelliennes) de la forme
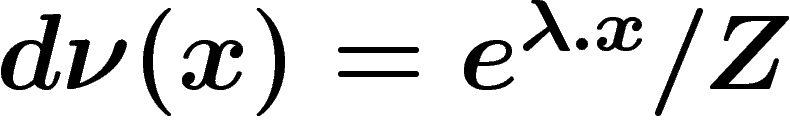 , où
, où 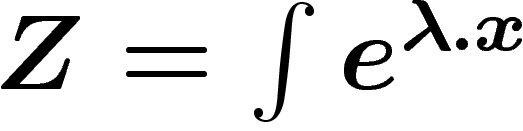 est la
constante de normalisation, appelée fonction de partition par les
physiciens. Ceci se démontre par un calcul variationnel simple, identique
à celui qui montre qu'à variance fixées, ce sont les gaussiennes.
est la
constante de normalisation, appelée fonction de partition par les
physiciens. Ceci se démontre par un calcul variationnel simple, identique
à celui qui montre qu'à variance fixées, ce sont les gaussiennes.
Soit 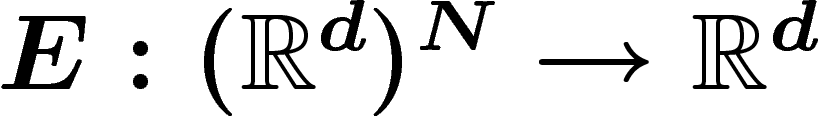 l'application « somme des
composantes ».
l'application « somme des
composantes ».
Pour minimiser l'entropie par rapport à la mesure 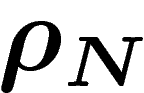 , il est donc
suffisant de chercher parmi les mesures de la forme
, il est donc
suffisant de chercher parmi les mesures de la forme
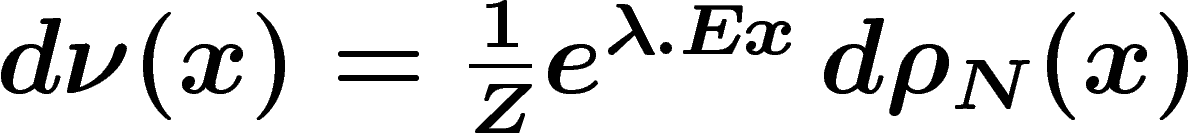 où
où 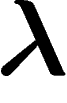 est un élément de
est un élément de
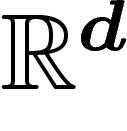 , le produit
, le produit 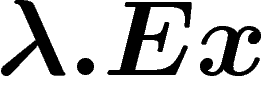 étant un produit scalaire. Cet élément
étant un produit scalaire. Cet élément
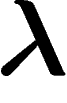 est à déterminer de sorte que la moyenne
est à déterminer de sorte que la moyenne 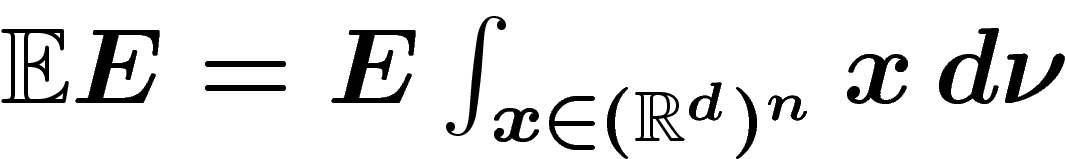 soit égale à Ny.
soit égale à Ny.
Ce qui nous intéresse est l'entropie de la distribution. Or pour les
distributions exponentielles, il y a une relation simple entre entropie
et moyenne. La moyenne de la distribution 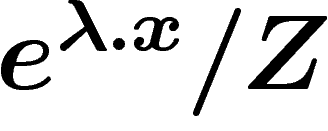 est
est 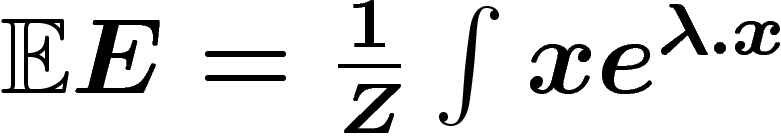 et son entropie est
et son entropie est 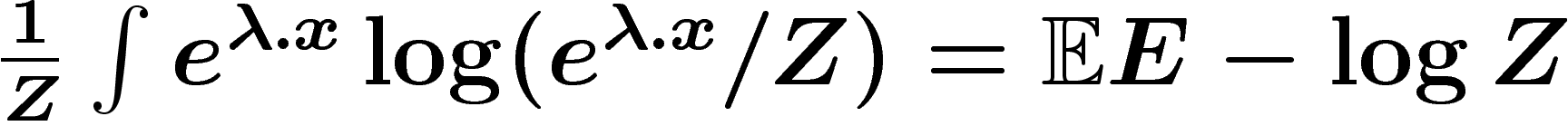 .
.
On voit donc qu'une distribution exponentielle de moyenne 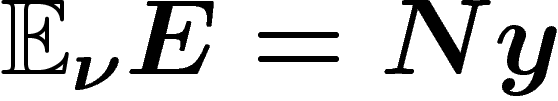 a une
entropie
a une
entropie 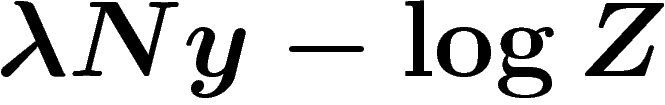 .
.
Reste quand même à déterminer 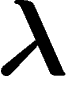 . Là encore la forme exponentielle
de la loi de probabilité joue : la dérivée de
. Là encore la forme exponentielle
de la loi de probabilité joue : la dérivée de 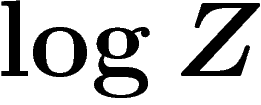 par
rapport à
par
rapport à 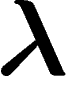 est précisément l'espérance de la distribution
exponentielle. En effet, on a
est précisément l'espérance de la distribution
exponentielle. En effet, on a
![\[\frac{d}{d\lambda}\log Z=
\frac1Z \frac{d}{d\lambda} \int e^{\lambda.x}=\frac1Z \int x e^{\lambda.x}
\]](entropie528.png)
Le 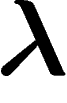 recherché vérifie donc
recherché vérifie donc 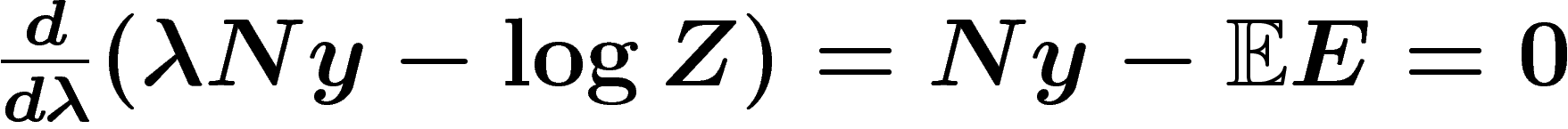 , autrement dit le
, autrement dit le 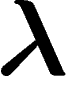 recherché est un extrémum de
recherché est un extrémum de
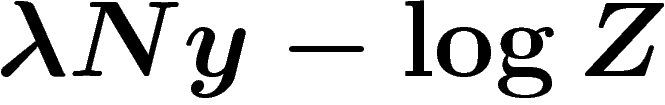 . C'est en fait un maximum car
. C'est en fait un maximum car 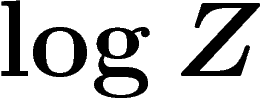 est une
fonction convexe de
est une
fonction convexe de 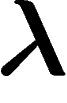 .
.
Dans le principe de grandes déviations 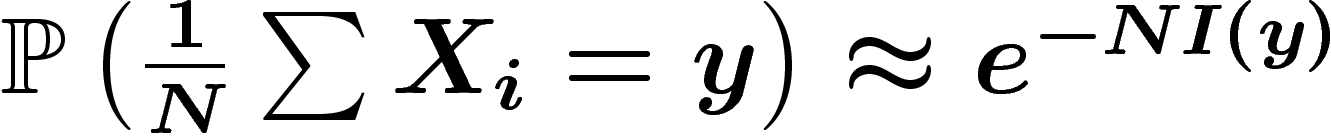 , on doit donc poser :
, on doit donc poser :
![\[
I(y)=\sup_{\lambda \in \R^d} \lambda.y - \frac1N \log Z(\lambda)
\]](entropie536.png)
![\[
Z(\lambda)=\int_{(t_1,\ldots,t_N)\in (\R^d)^N} \exp\left(\lambda \sum
t_i\right) \,d\rho_N(t_1,\ldots,t_N)
\]](entropie537.png)
On a donc réussi, grâce à la remarque que les minima d'entropie sont obtenus pour les distributions exponentielles, à donner une recette de calcul de l'entropie de l'événement « la moyenne est égale à y ».
Ceci nous amène donc à énoncer le théorème de Gärtner-Ellis. Cependant,
il faut faire attention à l'énoncé : par exemple, nos raisonnements
ci-dessus étaient à N fixé ; il faut donc que 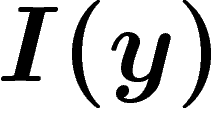 converge quand
converge quand 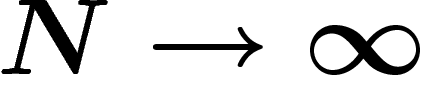 , vers une certaine valeur, ce qui ne
se produit que si les
, vers une certaine valeur, ce qui ne
se produit que si les 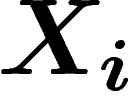 n'ont pas des distributions trop sauvages.
n'ont pas des distributions trop sauvages.
De plus, lorsque la limite 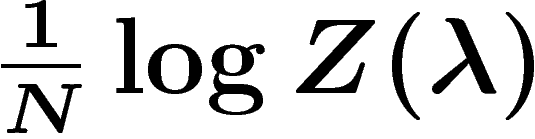 n'est pas
différentiable, il n'y a pas forcément de
n'est pas
différentiable, il n'y a pas forcément de 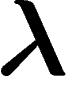 donnant une
exponentielle de moyenne y pour tout y, ce qui n'empêche pas que
donnant une
exponentielle de moyenne y pour tout y, ce qui n'empêche pas que
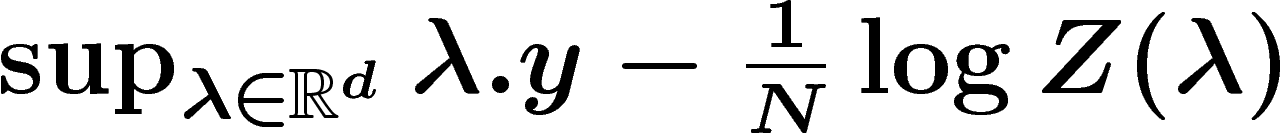 ait une
certaine valeur. Un même
ait une
certaine valeur. Un même 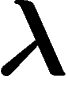 peut ainsi maximiser
peut ainsi maximiser 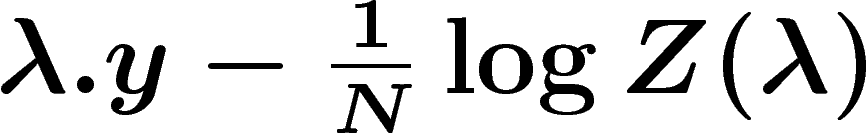 pour plusieurs y. Disons que
pour plusieurs y. Disons que 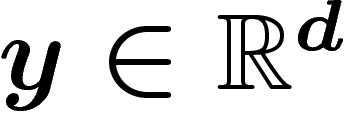 est
un point exposé si le
est
un point exposé si le 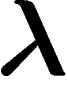 maximisant cette quantité ne maximise pas
aussi cette quantité pour un autre
maximisant cette quantité ne maximise pas
aussi cette quantité pour un autre 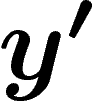 , cela revient à dire que y est
exposé s'il existe un
, cela revient à dire que y est
exposé s'il existe un 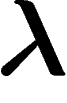 tel que pour tout
tel que pour tout 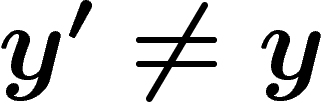 , on a
, on a
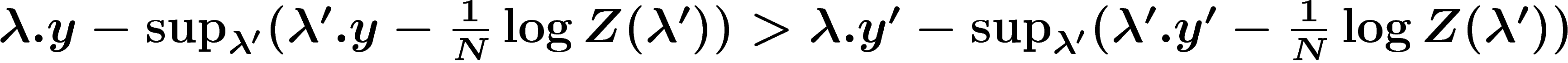 .
Les points exposés sont ceux pour lesquels le fait que
.
Les points exposés sont ceux pour lesquels le fait que 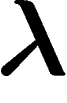 maximise
l'entropie implique bien que l'espérance de la distribution exponentielle
de paramètre
maximise
l'entropie implique bien que l'espérance de la distribution exponentielle
de paramètre 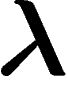 vaut y.
vaut y.
L'énoncé est alors le
suivant. Il se place dans un cadre un peu plus général où on ne considère
pas forcément une somme de variables aléatoires ; de plus, il se peut
que la bonne renormalisation ne soit pas N mais 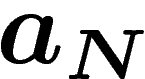 où
où 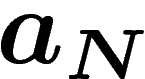 est une
suite tendant vers l'infini.
est une
suite tendant vers l'infini.
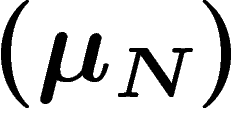 une suite de lois de probabilité sur
une suite de lois de probabilité sur 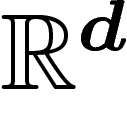 et soit
et soit 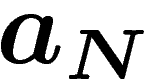 une suite tendant vers l'infini. Pour
une suite tendant vers l'infini. Pour 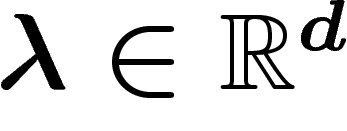 , on pose
, on pose
![\[
Z_N(\lambda)=\E_{\mu_N} e^{a_N\,\lambda.t}
\]](entropie560.png)
![\[
\Lambda(\lambda)=\lim_N \frac1{a_N}\log Z_N(\lambda)
\]](entropie561.png)
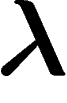 dans un voisinage de
dans un voisinage de  . Pour
. Pour
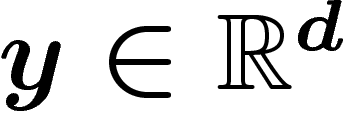 , soit
, soit
![\[
I(y)=\sup_{\lambda\in\R^d} \lambda.y-\Lambda(\lambda)
\]](entropie565.png)
 l'ensemble des points y exposés. Alors, si A
est une partie de
l'ensemble des points y exposés. Alors, si A
est une partie de 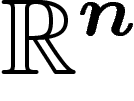 , d'adhérence
, d'adhérence  et d'intérieur
et d'intérieur
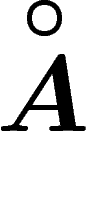 , on a
, on a
![\[
\vlimsup_N \frac1{a_N}\log \mu_N(A)\leq -\inf_{\overline{A}} I
\]](entropie570.png)
![\[
\vliminf_N\frac1{a_N}\log \mu_N(A)\geq -\inf_{\overset{\circ}A \cap
\mathcal{P}} I
\]](entropie571.png)
Reconnaissons que sans explication par la théorie de l'information, l'énoncé pourrait rester mystérieux.
Là encore, le sujet n'est pas clos : on peut chercher à montrer qu'un principe des grandes déviations est satisfait dans des contextes plus généraux (par exemple des chaînes de Markov), vouloir obtenir des bornes explicites plutôt que des relations asymptotiques, montrer que les grandes déviations sont contrôlées uniformément pour un grand nombre de fonctions-tests de la variable étudiée, ou encore étudier les innombrables et délicates applications à la physique statistique...