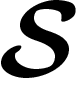 pouvant présenter un certain nombre
d'états. On a deux options de modélisation : la modélisation discrète, où
pouvant présenter un certain nombre
d'états. On a deux options de modélisation : la modélisation discrète, où
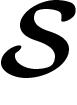 est un ensemble fini d'états
est un ensemble fini d'états  ; la modélisation continue,
où
; la modélisation continue,
où 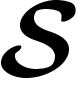 est une partie (compacte) de l'espace
est une partie (compacte) de l'espace 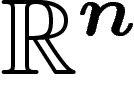 .
.
Ce texte entend expliquer la croyance populaire selon laquelle l'entropie augmenterait, qui semble incompatible avec la réversibilité des lois de la physique classique.
On analysera les situations classiques suivantes : une goutte d'encre versée dans un verre d'eau, un gaz initialement confiné dans une moitié de boîte et se répandant dans toute la boîte, ou encore une assiette qui tombe.
On essaiera d'expliquer comment le sens commun est capable de rejeter un film à l'envers de ces situations comme incompatible avec les lois de la physique, voire impossible.
On considère un système physique 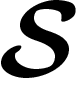 pouvant présenter un certain nombre
d'états. On a deux options de modélisation : la modélisation discrète, où
pouvant présenter un certain nombre
d'états. On a deux options de modélisation : la modélisation discrète, où
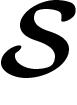 est un ensemble fini d'états
est un ensemble fini d'états  ; la modélisation continue,
où
; la modélisation continue,
où 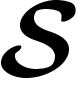 est une partie (compacte) de l'espace
est une partie (compacte) de l'espace 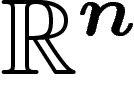 .
.
On suppose qu'on a un opérateur d'évolution temporelle 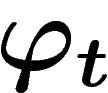 sur le
système. Dans le premier cas, pour t un nombre entier (positif ou
négatif),
sur le
système. Dans le premier cas, pour t un nombre entier (positif ou
négatif), 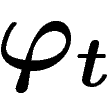 est une fonction de
est une fonction de 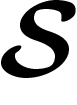 dans
dans 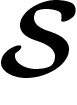 . La réversibilité
des lois de la physique signifie que
. La réversibilité
des lois de la physique signifie que 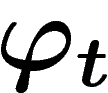 est une bijection, ce que
nous supposerons. Dans le cas continu, on suppose qu'on a une mesure de
volume sur l'espace des états (en mécanique classique elle est issue de
la forme symplectique
est une bijection, ce que
nous supposerons. Dans le cas continu, on suppose qu'on a une mesure de
volume sur l'espace des états (en mécanique classique elle est issue de
la forme symplectique  ), et que
), et que 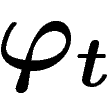 préserve le
volume : c'est l'analogue continu de la condition d'irréversibilité.
préserve le
volume : c'est l'analogue continu de la condition d'irréversibilité.
Notons qu'on a les relations 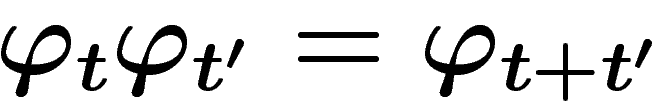 . Dans le cas
discret,
. Dans le cas
discret,  est entièrement déterminé à partir de
est entièrement déterminé à partir de 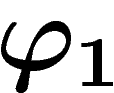 ; si le
temps est choisi continu, à partir de son générateur infinitésimal pour
; si le
temps est choisi continu, à partir de son générateur infinitésimal pour
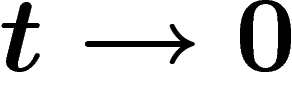 .
.
L'entropie microscopique d'un état d'un système discret est
définie comme le logarithme du nombre d'états de ce système accessibles à
partir de cet état par l'opérateur 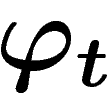 pour tout t.
L'entropie microscopique d'un état d'un système continu est
définie comme le logarithme du volume de (la fermeture topologique de)
l'ensemble des états accessibles par l'opérateur
pour tout t.
L'entropie microscopique d'un état d'un système continu est
définie comme le logarithme du volume de (la fermeture topologique de)
l'ensemble des états accessibles par l'opérateur 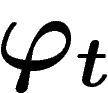 .
.
Comme l'ensemble des états accessibles par 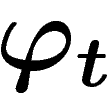 ne change pas si on
applique
ne change pas si on
applique 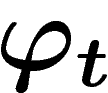 , les entropies microscopiques sont trivialement
indépendantes du temps : l'entropie microscopique est constante.
, les entropies microscopiques sont trivialement
indépendantes du temps : l'entropie microscopique est constante.
Par contre, si on change le système, l'entropie peut varier : si on a un
gaz dans une moitié de boîte, avec une paroi au milieu de la boîte, et
qu'on retire subitement la paroi, le nombre d'états accessibles au
système augmente d'un seul coup : lors du relâchement d'une
contrainte, l'entropie microscopique augmente. À noter que cette
augmentation se produit au moment où on enlève la paroi, même si le gaz
ne s'est pas encore répandu ; c'est l'opérateur d'évolution  qui a
changé.
qui a
changé.
L'entropie microscopique, qui tient compte de l'ensemble des états accessibles au système, n'est pas très satisfaisante (en particulier son changement subit lorsqu'on enlève la paroi, alors même que le gaz ne s'est pas encore répandu). Cependant, cette définition est largement suffisante pour une grande part de la physique statistique, fondée sur l'étude de la manière dont l'entropie d'un système dépend de son énergie.
L'entropie macroscopique, historiquement définie avant la précédente, ne possède pas cet inconvénient : elle ne dépend que de ce qu'on voit du système.
On suppose que les états de notre système sont répartis en un certain nombre de classes appelés états macroscopiques ou macro-états, deux états microscopiques appartenant au même macro-état s'ils ne peuvent pas être distingués par l'expérimentateur (éventuellement en utilisant certains appareils de mesure).
Par exemple, pour notre boîte de gaz, on peut définir les macro-états caractérisés par le nombre de particules de gaz dans les moitiés droite et gauche de la boîte. On peut aussi faire des distinctions plus fines si cela nous chaut.
Alors, l'entropie macroscopique d'un état microscopique est le logarithme du nombre d'états microscopiques correspondant au même macro-état (ou logarithme du volume, dans le cas continu). C'est ainsi une fonction de chaque macro-état.
L'entropie macroscopique globale du système peut être
définie comme la moyenne des entropies macroscopiques des états
microscopiques, autrement dit 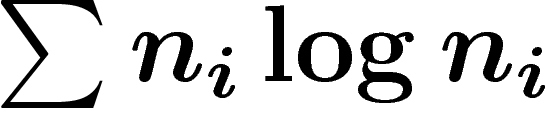 où
où 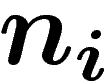 est le nombre
d'états microscopiques dans le macro-état i. On peut aussi normaliser
en
est le nombre
d'états microscopiques dans le macro-état i. On peut aussi normaliser
en 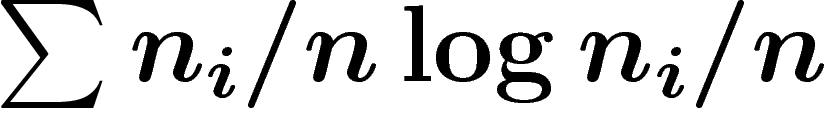 qui est la formule classique. Ceci est une
fonction globale qui ne dépend que du système, mais ni du temps ni d'un
état observé ; sa constance ou sa croissance n'a donc pas de sens
qui est la formule classique. Ceci est une
fonction globale qui ne dépend que du système, mais ni du temps ni d'un
état observé ; sa constance ou sa croissance n'a donc pas de sens
Si un des macro-états correspond à un nombre d'états microscopiques beaucoup plus grand que les autres, alors son entropie macroscopique est très proche de l'entropie microscopique du système. Ainsi ces deux définitions recouvrent souvent des notions comparables. Dans notre exemple de la boîte, de tels états sont ceux où les nombres de particules de gaz à droite et à gauche sont presque égaux. Une proportion presque totale des états microscopiques sont tels, et donc, le logarithme du macro-état correspondant est presque égal au logarithme du nombre d'états total du système.
Notons qu'au niveau macroscopique, la dynamique n'est plus définie que de manière probabiliste : si on a un macro-état, il manque de l'information, et il n'est pas sûr que tous les états microscopiques futurs issus du macro-état présent appartiennent au même macro-état futur.
Cependant :
(Les démonstrations de ces théorèmes, peu difficiles au moins dans le cas discret, sont omises. Toute fonction des états microscopiques vérifierait le premier qui n'est qu'une conséquence de la bijectivité. Toute fonction croissante du nombre d'états microscopiques dans un macro-état vérifierait le second.)
Illustrons ceci dans le cas de la goutte d'encre dans l'eau. Soit 1 le
nombre d'état où la goutte n'est pas diluée dans l'eau, et soit 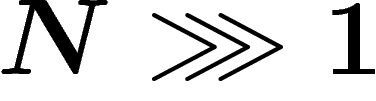 le nombre d'états où la goutte apparaît diluée. Alors, si on pose côte à
côte un verre avec goutte non diluée et un verre avec goutte diluée, la
goutte non diluée va se diluer, celle qui était diluée va tranquillement
le rester, et l'entropie aura augmenté.
le nombre d'états où la goutte apparaît diluée. Alors, si on pose côte à
côte un verre avec goutte non diluée et un verre avec goutte diluée, la
goutte non diluée va se diluer, celle qui était diluée va tranquillement
le rester, et l'entropie aura augmenté.
Par contre, si on place sur une très grande table N verres avec une goutte bien mélangée et 1 verre avec une goutte non diluée, en moyenne un des verres contiendra précisément la configuration microscopique des vitesses des particules d'encre requise pour qu'en une unité de temps, ces particules se regroupent pour former une belle goutte d'encre (une telle configuration existe forcément : il suffit d'inverser l'opérateur d'évolution à partir de l'état où la goutte est formée). Par conséquent, dans le verre où elle était présente la goutte d'encre disparaît, mais elle apparaît en moyenne dans un autre verre. L'entropie est constante en moyenne.
De même, à long terme, si on lâche une goutte d'encre dans un verre, elle commence par se diluer ; puis, au bout d'un nombre immense d'années, elle se reforme pour se diluer à nouveau immédiatement, et le cycle recommence pour les siècles des siècles. À long terme, l'entropie reste constante.
Le fait est qu'en pratique, on part plus souvent d'états à entropie plus faible que la moyenne ; par exemple on lâche l'encre au milieu du verre, ou encore, on place le gaz dans une moitié de boîte au moyen d'une paroi. Si on part souvent d'états à faible entropie, on a de bonnes chances que l'entropie augmente...
En voyant un film de scènes quotidiennes, on est parfaitement capable de dire si le film est passé à l'envers : on voit très couramment tomber des assiettes, mais moins souvent des morceaux d'assiette se soulever du sol pour bondir sur la table en formant une assiette complète. En revanche, un film de molécules de gaz s'entrechoquant, s'il pouvait être tourné, ne montrerait aucune dissymétrie temporelle. L'irréversibilité observée macroscopiquement est souvent attribuée à la croissance de l'entropie.
Comment, en pratique, reconnaissons-nous un film passé à l'envers ? Le raisonnement ne peut être purement déductif, puisque le film passé à l'envers est entièrement compatible avec toutes les lois de la physique, qui sont symétriques par renversement du temps (en physique classique ; les violations de symétrie par les particules élémentaires ne nous importent pas). Simplement, ce film apparaît comme extrêmement improbable. On mène en fait un raisonnement inductif, qui s'appuie sur le principe suivant, qui est un cas particulier d'une attitude beaucoup plus générale.
Reprenons nos N mélanges d'eau et d'encre de tout à l'heure. On nous
montre un film où, dans un verre contenant de l'encre et de l'eau, toute
l'encre se regroupe subitement et miraculeusement pour former une seule
goutte, au centre du verre. On suppose que le mélange initial d'encre et
d'eau était, au hasard, l'un des N tels mélanges possibles. On sait
qu'un exactement de ces mélanges donne une goutte bien formée au bout
d'une unité de temps, tandis que tous les autres restent aussi
insondables. Deux hypothèses : le film est à l'endroit, ou bien il est à
l'envers. Dans la première, le déroulement du film nous dit que nous nous
trouvions juste dans la configuration donnant une goutte, ce qui était a
priori le cas avec probabilité 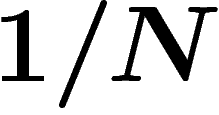 , le nombre N étant immense. Dans
le cas où le film est à l'envers, la goutte se dilue et cela n'a rien
d'anormal. Un raisonnement inductif amène donc à penser que l'hypothèse
que le film n'est pas truqué est à rejeter avec probabilité
, le nombre N étant immense. Dans
le cas où le film est à l'envers, la goutte se dilue et cela n'a rien
d'anormal. Un raisonnement inductif amène donc à penser que l'hypothèse
que le film n'est pas truqué est à rejeter avec probabilité 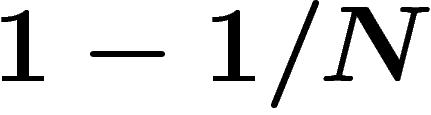 ,
autant dire
,
autant dire  vu la taille de N.
vu la taille de N.
La même interprétation vaut pour les assiettes sauteuses.
La thermodynamique classique, avec son second principe affirmant que l'entropie augmente, est pourtant tout à fait adaptée à la description d'un certain nombre de situations, tant en physique que dans la vie courante ; elle explique en particulier pourquoi, dans la réalité, les assiettes se brisent plus facilement qu'elles ne se forment spontanément (bien que si l'on considère l'univers dans son ensemble, plus d'assiettes aient été créées par l'action des lois de la physique que brisées...).
Une des formulations du second principe, une des plus anciennes historiquement est qu'on ne peut pas transformer la chaleur en travail dans un système où la température est uniforme. Chaleur et travail sont deux formes d'énergie ; la distinction entre les deux est que le travail est de l'énergie exploitable macroscopiquement, alors que la chaleur est de l'énergie non structurée d'agitation des molécules, qu'on ne peut pas exploiter (noter que la limite entre les deux dépend de la technologie disponible, en particulier pour l'exploitation de l'énergie chimique ou électrique).
Plus exactement, on peut transformer de la chaleur en travail, mais uniquement celle qu'on aurait préalablement produite en utilisant du travail (par exemple en brûlant un combustible), et en passant par un accroissement temporaire de la température d'une partie du système. On ne peut pas se contenter de refroidir un objet en pompant sa chaleur pour travailler.
Dans le cas des assiettes sauteuses, c'est l'énergie thermique du sol et de l'air, celle qui fait que l'assiette fait du bruit en tombant, qui serait récupérée pour faire s'envoler l'assiette. La chaleur ne peut pas être changée en travail.
Et pourtant :
Bien évidemment, cette recette n'est pas applicable en pratique étant donné la taille de N. On peut donc formuler ainsi le second principe de la thermodynamique : en pratique, on ne peut pas convertir de la chaleur en travail dans un système où la température est uniforme.
Ce principe est alors simplement une conséquence de la définition des états microscopiques correspondant à un même macro-état : par hypothèse, ce sont ceux qu'on ne peut pas distinguer, et a fortiori pas manipuler pour en extraire l'énergie.
On a vu que l'irréversibilité apparente à l'échelle macroscopique est le reflet des conditions particulières dans lesquelles on se place (on part plus souvent d'état de faible entropie) et du fait que l'homme ne peut pas spécifier toutes les caractéristiques microscopiques d'un état ; nul n'est besoin d'invoquer une dissymétrie fondamentale du temps, une loi macroscopique spécifique, ou encore l'indétermination de la mécanique quantique (dont les lois d'évolution sont d'ailleurs tout aussi réversibles que les lois classiques).
Nous n'avons nulle part utilisé la définition classique de l'entropie qui dit que sa variation est égale à la variation de chaleur divisée par la température. Notre cadre de départ était beaucoup trop général pour qu'une telle relation ait même un sens. Cependant, dans un certain nombre de systèmes physiques, les deux définitions coïncident ; nous ne donnerons pas la preuve de ce résultat découvert par Boltzmann, et qu'il fit graver sur sa tombe.