Back to: Main Page > Mathématiques
Le nombre d'extraterrestres
Introduction
On se propose ici d'apporter une réponse probabiliste aux trois petites
questions suivantes :
- Quelle sera la date de la fin du monde?
- Puis-je légitimement croire que les objets et personnes qui m'entourent sont le fruit de mon imagination?
- Combien d'extraterrestres y a-t-il dans l'Univers?
La formule de Bayes
(Thomas Bayes : mathématicien anglais 1702-1761).
On pourrait l'appeler "formule de probabilité des causes". C'est celle qui vous
dit que votre alarme dérange presque toujours les voisins pour rien, ou encore
que vous arrivez systématiquement dans un magasin au moment où la file
d'attente est le plus longue.
Si les événements 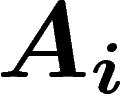 s'excluent mutuellement et recouvrent un univers donné,
connaissant les probabilités conditionnelles
s'excluent mutuellement et recouvrent un univers donné,
connaissant les probabilités conditionnelles 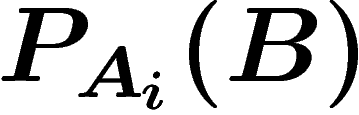 de réalisation de l'événement B
sachant
de réalisation de l'événement B
sachant 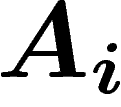 et les probabilités
et les probabilités 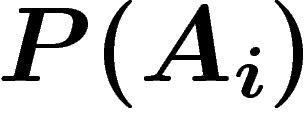 indépendamment de B, on peut calculer la
probabilité que sachant B, l'un des
indépendamment de B, on peut calculer la
probabilité que sachant B, l'un des 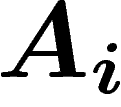 soit réalisé :
soit réalisé :
![\[
P_B(A_i)=\frac{P(A_i)P_{A_i}(B)}{\sum_j P(A_j)P_{A_j}(B)}
\]](extrater006.png)
Éventuellement, la somme sera remplacée par une intégrale dans le cas d'une variable continue.
Si donc la probabilité qu'une alarme se déclenche incongrûment durant
l'intervalle de temps dt est par exemple 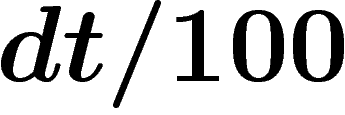 ,
celle qu'elle se déclenche en cas de vol est 1, et celle qu'il y ait un
vol durant l'intervalle dt est
,
celle qu'elle se déclenche en cas de vol est 1, et celle qu'il y ait un
vol durant l'intervalle dt est 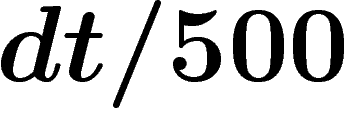 , la
probabilité qu'un déclenchement de l'alarme soit effectivement dû à un vol est
, la
probabilité qu'un déclenchement de l'alarme soit effectivement dû à un vol est
![\[
\frac{1\times\frac1{500}}{1\times\frac1{500}+\frac1{100}\times\frac{499}{500}}=\frac{100}{599}
\]](extrater009.png)
soit environ 1
chance sur 6, et pourtant les valeurs utilisées sont plutôt optimistes.
Cette formule peut servir à évaluer les probabilités de causes a priori
équiprobables sachant qu'un de leurs effets s'est produit.
Le dernier homme
Cette section reprend mathématiquement un raisonnement dû à
l'astrophysicien Brandon Carter et développé par le philosophe canadien
John Leslie (voir par exemple l'article de J.-P. Delahaye dans Pour la
Science n°191, sept. 93).
On suppose ici que le nombre de naissances humaines par unité de temps
vaut 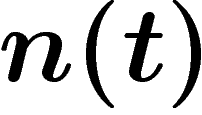 avec t en années, ceci en l'absence de disparition de
l'humanité. On supposera de plus que l'humanité est apparue vers l'année
avec t en années, ceci en l'absence de disparition de
l'humanité. On supposera de plus que l'humanité est apparue vers l'année
 (ce qui, vu le nombre d'hommes à cette époque dans les modèles
envisagés, ne change pas fondamentalement le résultat). Dans ces
conditions, le nombre d'hommes ayant vécu sur terre jusqu'à l'année t
est
(ce qui, vu le nombre d'hommes à cette époque dans les modèles
envisagés, ne change pas fondamentalement le résultat). Dans ces
conditions, le nombre d'hommes ayant vécu sur terre jusqu'à l'année t
est 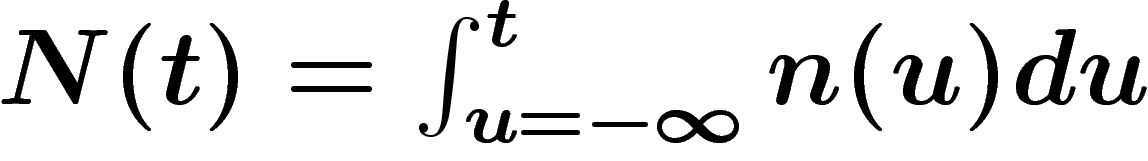 . Si l'humanité disparaît précocement
l'année
. Si l'humanité disparaît précocement
l'année 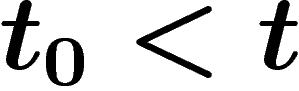 , le nombre total d'hommes ayant vécu sur terre est un
chouia moins que
, le nombre total d'hommes ayant vécu sur terre est un
chouia moins que 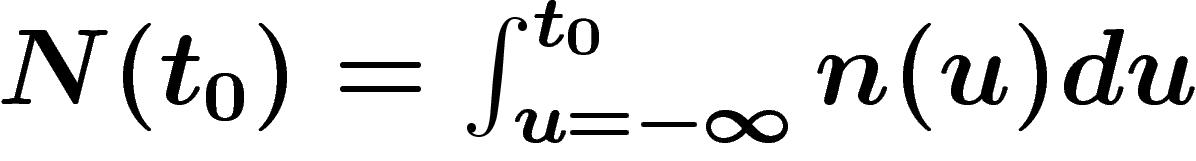 . Le chouia moins
est dû au fait que la disparition n'est pas instantanée. En fait dans la
suite on aura besoin d'une minoration plutôt que d'une majoration ; on
peut pallier à cet inconvénient en appelant
. Le chouia moins
est dû au fait que la disparition n'est pas instantanée. En fait dans la
suite on aura besoin d'une minoration plutôt que d'une majoration ; on
peut pallier à cet inconvénient en appelant 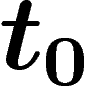 l'année où pour la
première fois
l'année où pour la
première fois 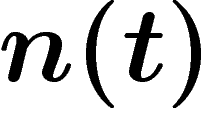 est plus faible que ce que prévoit le modèle sans
disparition (on pourrait poser
est plus faible que ce que prévoit le modèle sans
disparition (on pourrait poser 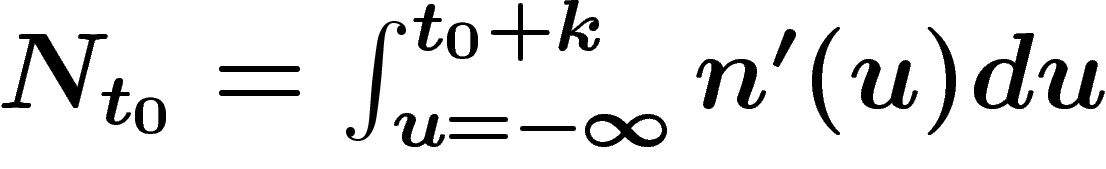 où
où 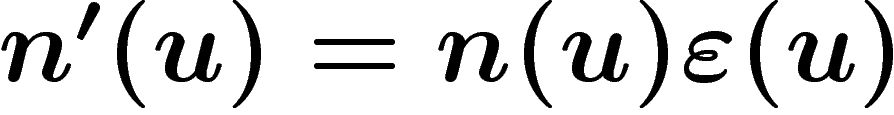 avec
avec  égal à 1 avant
égal à 1 avant 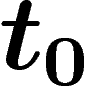 et valant 0 après
la date
et valant 0 après
la date 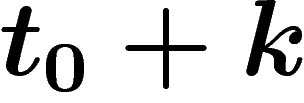 , et supposer que k est petit).
, et supposer que k est petit).
Dans ces conditions, on peut calculer la proportion d'hommes nés l'année
T [mettez ici votre année de naissance], c'est-à-dire la probabilité
qu'un homme choisi au hasard soit né en T. Si 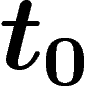 est la date de
disparition de l'humanité (éventuellement infinie), cette quantité vaut
est la date de
disparition de l'humanité (éventuellement infinie), cette quantité vaut
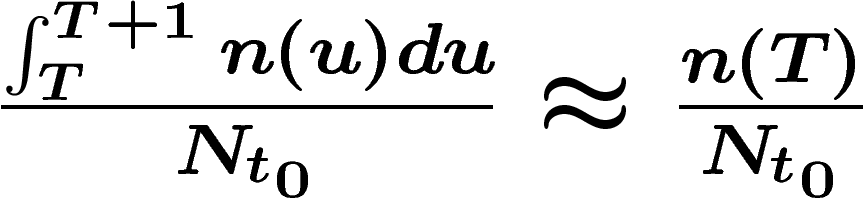 sachant que les variations de n sont faibles durant l'année considérée.
Appliquez maintenant la formule de Bayes à vous-mêmes pour l'événement
"être né l'année T", selon la date de disparition de l'humanité. Ceci
revient à appliquer le principe anthropique : "un observateur a plus de
chances de se trouver là où les observateurs sont le plus probables" (à
noter que l'inventeur de l'expression "principe anthropique" n'est autre
que Brandon Carter, même s'il semblerait que l'usage ultérieur de ces
termes ait largement dépassé son idée initiale).
sachant que les variations de n sont faibles durant l'année considérée.
Appliquez maintenant la formule de Bayes à vous-mêmes pour l'événement
"être né l'année T", selon la date de disparition de l'humanité. Ceci
revient à appliquer le principe anthropique : "un observateur a plus de
chances de se trouver là où les observateurs sont le plus probables" (à
noter que l'inventeur de l'expression "principe anthropique" n'est autre
que Brandon Carter, même s'il semblerait que l'usage ultérieur de ces
termes ait largement dépassé son idée initiale).
Les dates de disparition de l'humanité sont toutes a priori équiprobables (sauf celles antérieures à 1997). Sachant que
vous êtes né l'année T, la probabilité que l'humanité disparaisse
l'année 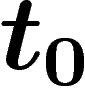 (ou plus exactement la probabilité
instantanée de disparition entre
(ou plus exactement la probabilité
instantanée de disparition entre 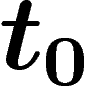 et
et 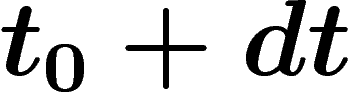 , ramenée à une année) est
, ramenée à une année) est
![\[
p(t_0)=\frac{\frac{n(T)}{N_{t_0}}}{\int_{u=1997}^\infty
\frac{n(T)}{N_u}du}=\frac{1}{N_{t_0}\int_{u=1997}^\infty}\frac{du}{N_u}
\]](extrater027.png)
(en bon
matheux, on vérifie placidement que la somme des probabilités de disparition de l'humanité de 1997 à l'infini vaut
bien 1).
On peut calculer le résultat pour différents modèles d'évolution de la
population. Prenons par exemple un modèle exponentiel avec un exposant de
l'ordre de 0.013/année, ce qui correspond aux données actuelles
(doublement de la population tous les 50 ans environ). Le coefficient
multiplicatif constant n'intervient pas dans le résultat final, et peut
donc être pris égal à 1. Alors 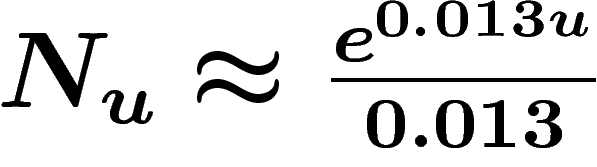 et
et
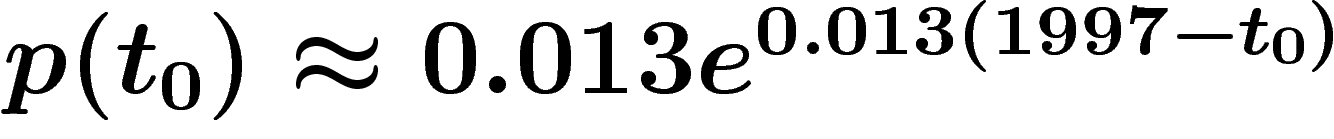 ce qui donne 1,3% pour l'année
prochaine. Si on prend plutôt un modèle d'évolution de la population
sous la forme
ce qui donne 1,3% pour l'année
prochaine. Si on prend plutôt un modèle d'évolution de la population
sous la forme 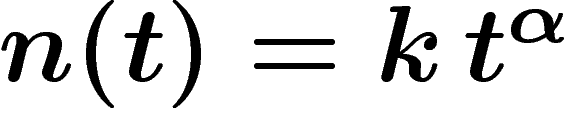 , en négligeant les dates négatives, tous
calculs faits
, en négligeant les dates négatives, tous
calculs faits 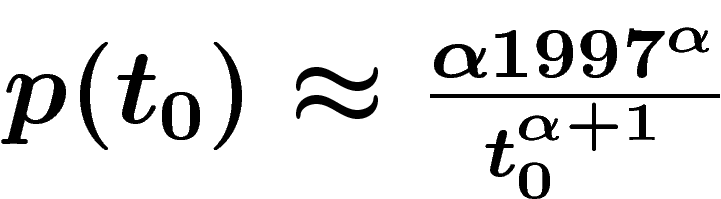 (le fait que cette valeur puisse dépasser 1 pour
(le fait que cette valeur puisse dépasser 1 pour 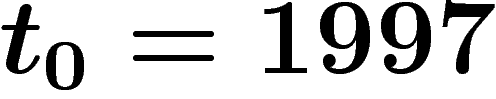 provient de
l'approximation de discrétisation, utilisée deux fois dans ce
raisonnement, qui consiste à dire que
provient de
l'approximation de discrétisation, utilisée deux fois dans ce
raisonnement, qui consiste à dire que 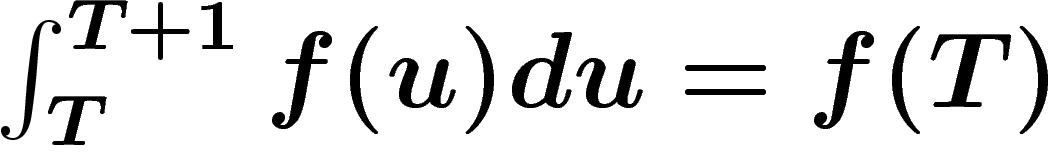 ). Pour un
exposant ajusté sur les données actuelles, aux environs de 11 (avec une
belle marge d'erreur), la probabilité est aux alentours de 0,5% pour
l'année prochaine. Il convient de rappeler que la non-nullité de la durée
de l'agonie entraîne une légère sous-évaluation des N calculés et donc de
ces probabilités.
). Pour un
exposant ajusté sur les données actuelles, aux environs de 11 (avec une
belle marge d'erreur), la probabilité est aux alentours de 0,5% pour
l'année prochaine. Il convient de rappeler que la non-nullité de la durée
de l'agonie entraîne une légère sous-évaluation des N calculés et donc de
ces probabilités.
Restent cependant les cas de divergence l'intégrale 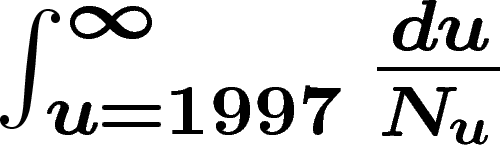 . Ceci ne se produit que si
. Ceci ne se produit que si 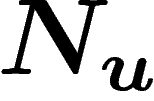 ne croît pas trop vite
(dans le style
ne croît pas trop vite
(dans le style 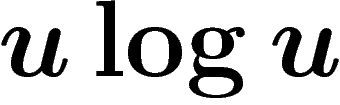 ). Mais maintenant si n décroît (si
). Mais maintenant si n décroît (si 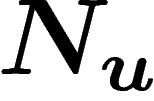 croît
moins vite que u), comme il est entier, il finira par atteindre 0 pour
une date
croît
moins vite que u), comme il est entier, il finira par atteindre 0 pour
une date 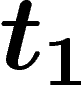 ; alors, dans la formule de Bayes, on doit prendre
l'intégrale non plus jusqu'à l'infini mais jusqu'à
; alors, dans la formule de Bayes, on doit prendre
l'intégrale non plus jusqu'à l'infini mais jusqu'à 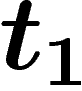 , puisque les dates
ultérieures sont a priori exclues, et l'intégrale retrouve une valeur
finie, donc la probabilité de disparition l'année prochaine reprend une
valeur non nulle. Nos descendants, sous peine de nous voir disparaître
avant l'heure (et donc eux avec nous), devront donc fixer leurs
naissances avec une grande précision (quoiqu'en fait, ils pourront
toujours laisser à la génération suivante le soin de rectifier le tir, et
ainsi jusqu'à l'infini s'ils ne disparaissent pas).
, puisque les dates
ultérieures sont a priori exclues, et l'intégrale retrouve une valeur
finie, donc la probabilité de disparition l'année prochaine reprend une
valeur non nulle. Nos descendants, sous peine de nous voir disparaître
avant l'heure (et donc eux avec nous), devront donc fixer leurs
naissances avec une grande précision (quoiqu'en fait, ils pourront
toujours laisser à la génération suivante le soin de rectifier le tir, et
ainsi jusqu'à l'infini s'ils ne disparaissent pas).
L'homme seul
Un raisonnement de la même veine peut fournir une réfutation du
scepticisme. S'il y a exactement n êtres pensants dans l'univers, la
probabilité que l'un d'eux, choisi au hasard, soit moi est 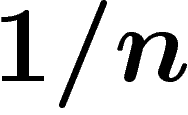 . Maintenant,
sachant que je suis moi, la probabilité que cela provienne du fait qu'il
n'existe que moi dans l'univers est, d'après la formule de Bayes, si on
considère qu'a priori toutes les possibilités sont équiprobables :
. Maintenant,
sachant que je suis moi, la probabilité que cela provienne du fait qu'il
n'existe que moi dans l'univers est, d'après la formule de Bayes, si on
considère qu'a priori toutes les possibilités sont équiprobables :
![\[
\frac{1}{\sum_1^\infty \frac{1}{n}}=0
\]](extrater041.png)
Cela signifie que la probabilité que je sois seul dans l'univers est
nulle. En fait ce raisonnement est faussé car il se base sur une densité
a priori uniforme sur 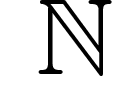 ... ce qui est impossible. On peut lever cet
inconvénient en appelant N le nombre maximal d'êtres pensants que
l'univers peut accueillir, et en faisant l'hypothèse d'une répartition
uniforme entre 1 et N. Ceci permet de ne sommer que de 1 à N et donc
d'obtenir la valeur
... ce qui est impossible. On peut lever cet
inconvénient en appelant N le nombre maximal d'êtres pensants que
l'univers peut accueillir, et en faisant l'hypothèse d'une répartition
uniforme entre 1 et N. Ceci permet de ne sommer que de 1 à N et donc
d'obtenir la valeur 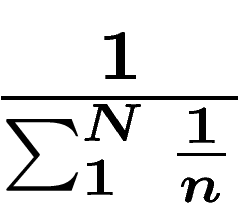 qui vaut environ
qui vaut environ
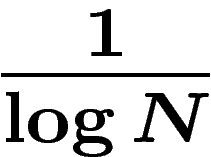 si N est grand (ce qui est certainement le cas). On
estime qu'actuellement le nombre de particules dans l'univers observable
est environ
si N est grand (ce qui est certainement le cas). On
estime qu'actuellement le nombre de particules dans l'univers observable
est environ 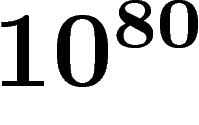 , ce qui limite N à cette valeur (et probablement
bien en deçà) et donc
, ce qui limite N à cette valeur (et probablement
bien en deçà) et donc  ce qui donne une probabilité non
négligeable d'être seul. Je peux cependant me demander quelle valeur je
dois accorder aux estimations des physiciens si je crois qu'ils ne sont
que des images mentales.
ce qui donne une probabilité non
négligeable d'être seul. Je peux cependant me demander quelle valeur je
dois accorder aux estimations des physiciens si je crois qu'ils ne sont
que des images mentales.
Maintenant que j'y pense, les résultats de la section précédente
utilisaient une densité uniforme sur 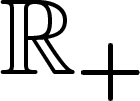 , ce qui n'est guère plus
possible que sur
, ce qui n'est guère plus
possible que sur 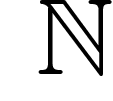 . Pour éviter cela, il suffit de la même manière de
borner la durée de vie de notre civilisation (par exemple par la mort du
Soleil dans 5 milliards d'années, ou par la durée que mettra notre espèce
à muter en une autre). Vu les intégrales à prendre en compte, cela ne
doit pas beaucoup modifier les résultats numériques (et d'ailleurs plutôt
à la hausse) dans les cas exponentiel et polynomial, et cela restitue une
valeur non nulle à la probabilité dans les cas où celle-ci était nulle
(et dans ce cadre, d'ailleurs, le contre-argument du report du contrôle
sur la génération suivante ne tient plus puisque le temps est borné).
. Pour éviter cela, il suffit de la même manière de
borner la durée de vie de notre civilisation (par exemple par la mort du
Soleil dans 5 milliards d'années, ou par la durée que mettra notre espèce
à muter en une autre). Vu les intégrales à prendre en compte, cela ne
doit pas beaucoup modifier les résultats numériques (et d'ailleurs plutôt
à la hausse) dans les cas exponentiel et polynomial, et cela restitue une
valeur non nulle à la probabilité dans les cas où celle-ci était nulle
(et dans ce cadre, d'ailleurs, le contre-argument du report du contrôle
sur la génération suivante ne tient plus puisque le temps est borné).
... et les autres
Appliquons strictement le même raisonnement à une situation légèrement
différente : sachant que nous sommes au moins n dans l'univers (les 5
milliards présents sur terre actuellement), combien d'extraterrestres y
a-t-il? S'il y a p êtres pensants dans l'univers, la probabilité que
n choisis au hasard soient précisément les n que je connais est
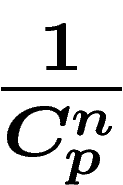 . La formule de Bayes donne alors, avec le même N que
précédemment (qui cette fois-ci ne tombe pas sous la critique de
l'inexistence des physiciens), que la probabilité que nous soyons seuls
dans l'univers est
. La formule de Bayes donne alors, avec le même N que
précédemment (qui cette fois-ci ne tombe pas sous la critique de
l'inexistence des physiciens), que la probabilité que nous soyons seuls
dans l'univers est
![\[ \frac{1}{\sum_{p=n}^N\frac1{C_p^n}} \]](extrater050.png)
qui, sachant
que N est très grand et que la série 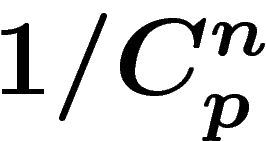 converge très vite pour
converge très vite pour
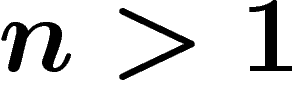 , est très proche de
, est très proche de 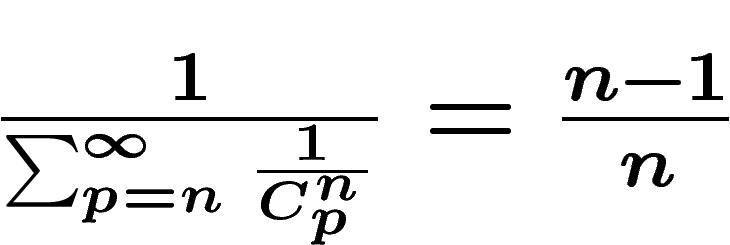 (voir en annexe une ébauche de preuve de
cette dernière égalité), ce qui laisse 1 chance sur n (n=5 milliards)
qu'il y ait des extraterrestres.
(voir en annexe une ébauche de preuve de
cette dernière égalité), ce qui laisse 1 chance sur n (n=5 milliards)
qu'il y ait des extraterrestres.
On pourra opposer que les probabilités de choix "au hasard" des n êtres
pensants parmi p ne sont pas indépendantes et qu'on a tendance à
choisir des êtres pensants ayant dans l'univers une localisation
géographique relativement proche. Le 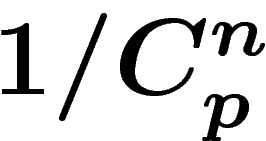 doit donc être revu à la hausse,
ce qui augmente la probabilité d'existence des extraterrestres.
doit donc être revu à la hausse,
ce qui augmente la probabilité d'existence des extraterrestres.
En guise de conclusion
Je ne m'excuse pas auprès du lecteur des éventuelles nuits blanches occasionnées par la lecture de ces lignes, car c'est
sciemment que je ne l'avais pas averti de ce risque en début d'article, afin de ne pas le dissuader de contribuer à
l'avancement de la science.
Annexe
Voici les grandes lignes d'une preuve de 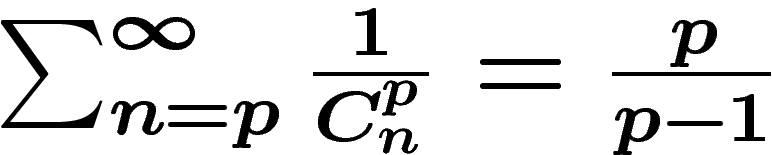 .
.
On commence d'abord par montrer (une récurrence marche) que
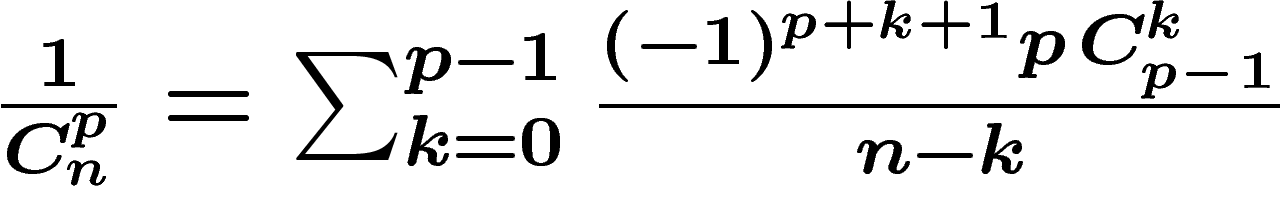 , ce
qui constitue une belle simplification dans la mesure où, ajoutant ces
quantités pour n variant de p à l'infini, on a des télescopages massifs
qui permettent de réduire l'expression
, ce
qui constitue une belle simplification dans la mesure où, ajoutant ces
quantités pour n variant de p à l'infini, on a des télescopages massifs
qui permettent de réduire l'expression 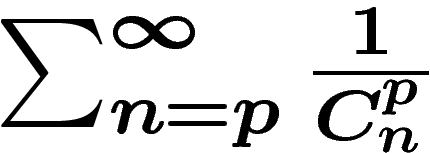 à disséquer à la valeur nettement
plus agréable
à disséquer à la valeur nettement
plus agréable
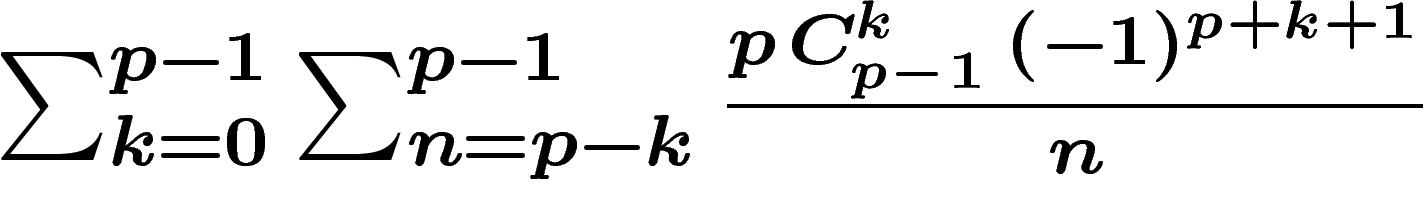 . Une partie de cette expression peut être calculée à
partir de la valeur d'une autre partie au rang précédent, ce qui donne
après moult calcul que cette expression vaut aussi
. Une partie de cette expression peut être calculée à
partir de la valeur d'une autre partie au rang précédent, ce qui donne
après moult calcul que cette expression vaut aussi
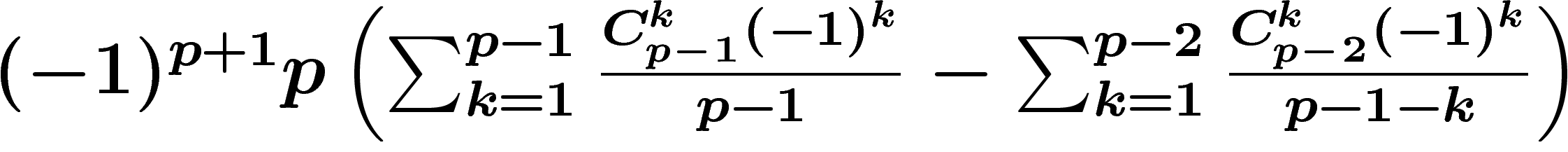 . Le premier terme se
simplifie immédiatement grâce à la formule du binôme. Le second nécessite
de séparer les cas pair et impair et d'utiliser des scissions puis
recoupements d'indices conjointement avec maintes propriétés des
coefficients binomiaux. Tout un programme.
. Le premier terme se
simplifie immédiatement grâce à la formule du binôme. Le second nécessite
de séparer les cas pair et impair et d'utiliser des scissions puis
recoupements d'indices conjointement avec maintes propriétés des
coefficients binomiaux. Tout un programme.
Back to: Main Page > Mathématiques
To leave a comment: contact (domain) yann-ollivier.org
 s'excluent mutuellement et recouvrent un univers donné,
connaissant les probabilités conditionnelles
s'excluent mutuellement et recouvrent un univers donné,
connaissant les probabilités conditionnelles 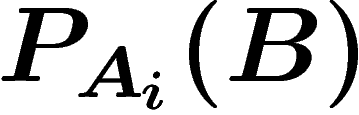 de réalisation de l'événement B
sachant
de réalisation de l'événement B
sachant 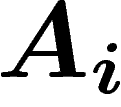 et les probabilités
et les probabilités 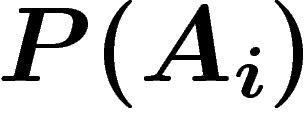 indépendamment de B, on peut calculer la
probabilité que sachant B, l'un des
indépendamment de B, on peut calculer la
probabilité que sachant B, l'un des 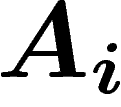 soit réalisé :
soit réalisé :
![\[
P_B(A_i)=\frac{P(A_i)P_{A_i}(B)}{\sum_j P(A_j)P_{A_j}(B)}
\]](extrater006.png)
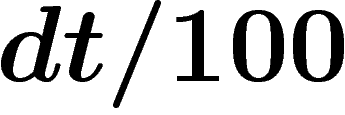 ,
celle qu'elle se déclenche en cas de vol est 1, et celle qu'il y ait un
vol durant l'intervalle dt est
,
celle qu'elle se déclenche en cas de vol est 1, et celle qu'il y ait un
vol durant l'intervalle dt est 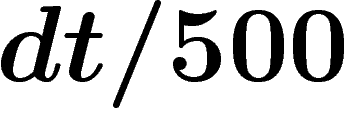 , la
probabilité qu'un déclenchement de l'alarme soit effectivement dû à un vol est
, la
probabilité qu'un déclenchement de l'alarme soit effectivement dû à un vol est
![\[
\frac{1\times\frac1{500}}{1\times\frac1{500}+\frac1{100}\times\frac{499}{500}}=\frac{100}{599}
\]](extrater009.png)
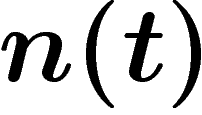 avec t en années, ceci en l'absence de disparition de
l'humanité. On supposera de plus que l'humanité est apparue vers l'année
avec t en années, ceci en l'absence de disparition de
l'humanité. On supposera de plus que l'humanité est apparue vers l'année
 (ce qui, vu le nombre d'hommes à cette époque dans les modèles
envisagés, ne change pas fondamentalement le résultat). Dans ces
conditions, le nombre d'hommes ayant vécu sur terre jusqu'à l'année t
est
(ce qui, vu le nombre d'hommes à cette époque dans les modèles
envisagés, ne change pas fondamentalement le résultat). Dans ces
conditions, le nombre d'hommes ayant vécu sur terre jusqu'à l'année t
est 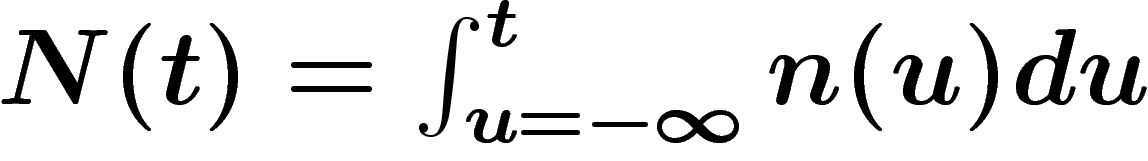 . Si l'humanité disparaît précocement
l'année
. Si l'humanité disparaît précocement
l'année  , le nombre total d'hommes ayant vécu sur terre est un
chouia moins que
, le nombre total d'hommes ayant vécu sur terre est un
chouia moins que 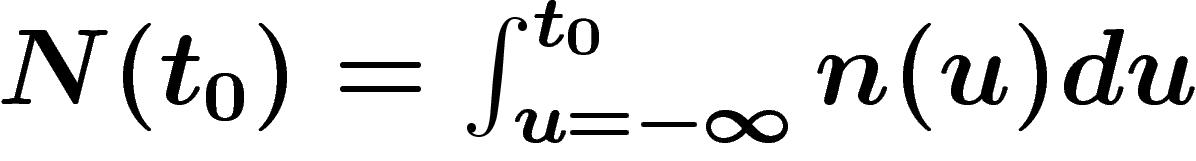 . Le chouia moins
est dû au fait que la disparition n'est pas instantanée. En fait dans la
suite on aura besoin d'une minoration plutôt que d'une majoration ; on
peut pallier à cet inconvénient en appelant
. Le chouia moins
est dû au fait que la disparition n'est pas instantanée. En fait dans la
suite on aura besoin d'une minoration plutôt que d'une majoration ; on
peut pallier à cet inconvénient en appelant 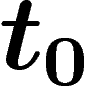 l'année où pour la
première fois
l'année où pour la
première fois 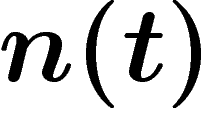 est plus faible que ce que prévoit le modèle sans
disparition (on pourrait poser
est plus faible que ce que prévoit le modèle sans
disparition (on pourrait poser 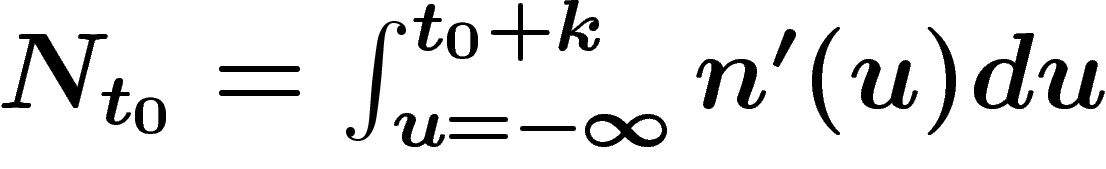 où
où 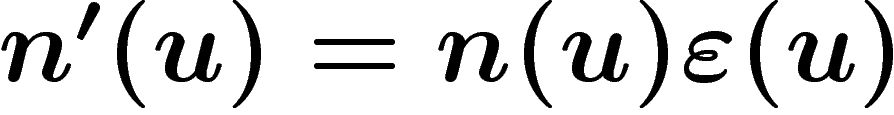 avec
avec  égal à 1 avant
égal à 1 avant 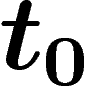 et valant 0 après
la date
et valant 0 après
la date 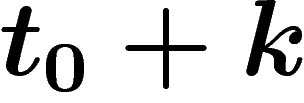 , et supposer que k est petit).
, et supposer que k est petit).
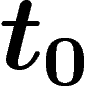 est la date de
disparition de l'humanité (éventuellement infinie), cette quantité vaut
est la date de
disparition de l'humanité (éventuellement infinie), cette quantité vaut
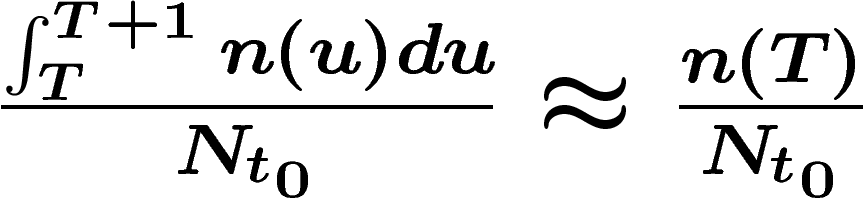 sachant que les variations de n sont faibles durant l'année considérée.
Appliquez maintenant la formule de Bayes à vous-mêmes pour l'événement
"être né l'année T", selon la date de disparition de l'humanité. Ceci
revient à appliquer le principe anthropique : "un observateur a plus de
chances de se trouver là où les observateurs sont le plus probables" (à
noter que l'inventeur de l'expression "principe anthropique" n'est autre
que Brandon Carter, même s'il semblerait que l'usage ultérieur de ces
termes ait largement dépassé son idée initiale).
sachant que les variations de n sont faibles durant l'année considérée.
Appliquez maintenant la formule de Bayes à vous-mêmes pour l'événement
"être né l'année T", selon la date de disparition de l'humanité. Ceci
revient à appliquer le principe anthropique : "un observateur a plus de
chances de se trouver là où les observateurs sont le plus probables" (à
noter que l'inventeur de l'expression "principe anthropique" n'est autre
que Brandon Carter, même s'il semblerait que l'usage ultérieur de ces
termes ait largement dépassé son idée initiale).
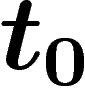 (ou plus exactement la probabilité
instantanée de disparition entre
(ou plus exactement la probabilité
instantanée de disparition entre 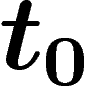 et
et 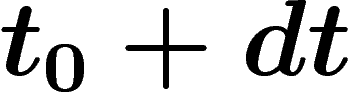 , ramenée à une année) est
, ramenée à une année) est
![\[
p(t_0)=\frac{\frac{n(T)}{N_{t_0}}}{\int_{u=1997}^\infty
\frac{n(T)}{N_u}du}=\frac{1}{N_{t_0}\int_{u=1997}^\infty}\frac{du}{N_u}
\]](extrater027.png)
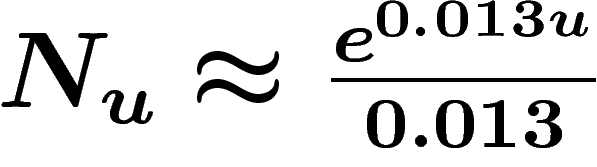 et
et
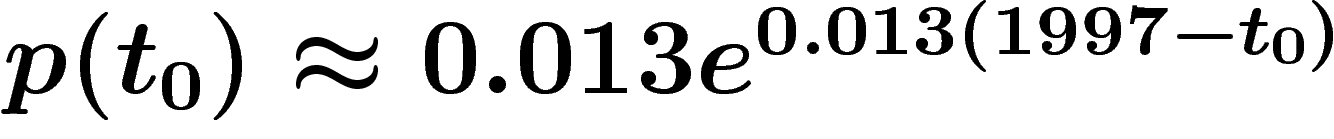 ce qui donne 1,3% pour l'année
prochaine. Si on prend plutôt un modèle d'évolution de la population
sous la forme
ce qui donne 1,3% pour l'année
prochaine. Si on prend plutôt un modèle d'évolution de la population
sous la forme 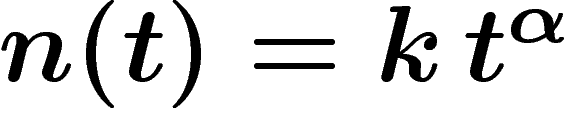 , en négligeant les dates négatives, tous
calculs faits
, en négligeant les dates négatives, tous
calculs faits 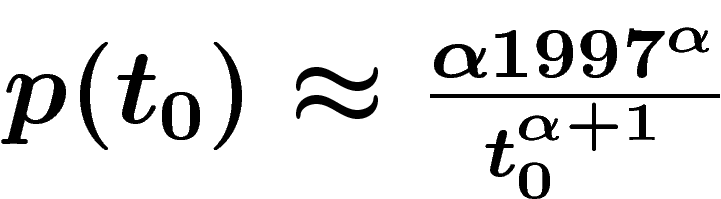 (le fait que cette valeur puisse dépasser 1 pour
(le fait que cette valeur puisse dépasser 1 pour 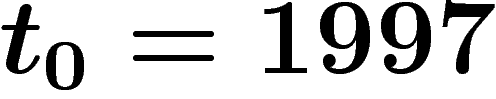 provient de
l'approximation de discrétisation, utilisée deux fois dans ce
raisonnement, qui consiste à dire que
provient de
l'approximation de discrétisation, utilisée deux fois dans ce
raisonnement, qui consiste à dire que 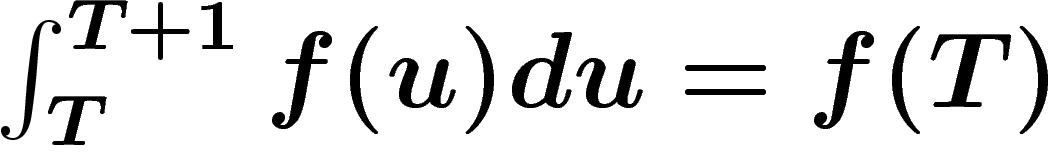 ). Pour un
exposant ajusté sur les données actuelles, aux environs de 11 (avec une
belle marge d'erreur), la probabilité est aux alentours de 0,5% pour
l'année prochaine. Il convient de rappeler que la non-nullité de la durée
de l'agonie entraîne une légère sous-évaluation des N calculés et donc de
ces probabilités.
). Pour un
exposant ajusté sur les données actuelles, aux environs de 11 (avec une
belle marge d'erreur), la probabilité est aux alentours de 0,5% pour
l'année prochaine. Il convient de rappeler que la non-nullité de la durée
de l'agonie entraîne une légère sous-évaluation des N calculés et donc de
ces probabilités.
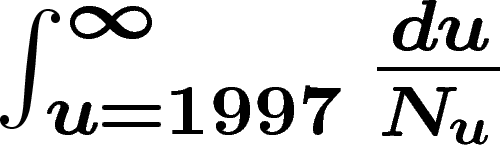 . Ceci ne se produit que si
. Ceci ne se produit que si 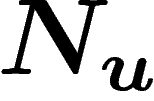 ne croît pas trop vite
(dans le style
ne croît pas trop vite
(dans le style 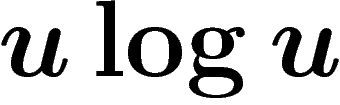 ). Mais maintenant si n décroît (si
). Mais maintenant si n décroît (si 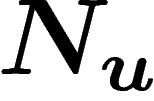 croît
moins vite que u), comme il est entier, il finira par atteindre 0 pour
une date
croît
moins vite que u), comme il est entier, il finira par atteindre 0 pour
une date 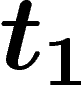 ; alors, dans la formule de Bayes, on doit prendre
l'intégrale non plus jusqu'à l'infini mais jusqu'à
; alors, dans la formule de Bayes, on doit prendre
l'intégrale non plus jusqu'à l'infini mais jusqu'à 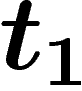 , puisque les dates
ultérieures sont a priori exclues, et l'intégrale retrouve une valeur
finie, donc la probabilité de disparition l'année prochaine reprend une
valeur non nulle. Nos descendants, sous peine de nous voir disparaître
avant l'heure (et donc eux avec nous), devront donc fixer leurs
naissances avec une grande précision (quoiqu'en fait, ils pourront
toujours laisser à la génération suivante le soin de rectifier le tir, et
ainsi jusqu'à l'infini s'ils ne disparaissent pas).
, puisque les dates
ultérieures sont a priori exclues, et l'intégrale retrouve une valeur
finie, donc la probabilité de disparition l'année prochaine reprend une
valeur non nulle. Nos descendants, sous peine de nous voir disparaître
avant l'heure (et donc eux avec nous), devront donc fixer leurs
naissances avec une grande précision (quoiqu'en fait, ils pourront
toujours laisser à la génération suivante le soin de rectifier le tir, et
ainsi jusqu'à l'infini s'ils ne disparaissent pas).
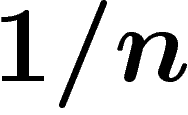 . Maintenant,
sachant que je suis moi, la probabilité que cela provienne du fait qu'il
n'existe que moi dans l'univers est, d'après la formule de Bayes, si on
considère qu'a priori toutes les possibilités sont équiprobables :
. Maintenant,
sachant que je suis moi, la probabilité que cela provienne du fait qu'il
n'existe que moi dans l'univers est, d'après la formule de Bayes, si on
considère qu'a priori toutes les possibilités sont équiprobables :
![\[
\frac{1}{\sum_1^\infty \frac{1}{n}}=0
\]](extrater041.png)
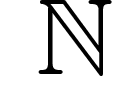 ... ce qui est impossible. On peut lever cet
inconvénient en appelant N le nombre maximal d'êtres pensants que
l'univers peut accueillir, et en faisant l'hypothèse d'une répartition
uniforme entre 1 et N. Ceci permet de ne sommer que de 1 à N et donc
d'obtenir la valeur
... ce qui est impossible. On peut lever cet
inconvénient en appelant N le nombre maximal d'êtres pensants que
l'univers peut accueillir, et en faisant l'hypothèse d'une répartition
uniforme entre 1 et N. Ceci permet de ne sommer que de 1 à N et donc
d'obtenir la valeur 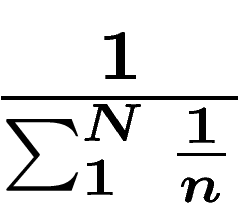 qui vaut environ
qui vaut environ
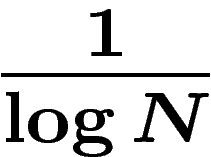 si N est grand (ce qui est certainement le cas). On
estime qu'actuellement le nombre de particules dans l'univers observable
est environ
si N est grand (ce qui est certainement le cas). On
estime qu'actuellement le nombre de particules dans l'univers observable
est environ 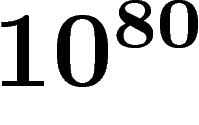 , ce qui limite N à cette valeur (et probablement
bien en deçà) et donc
, ce qui limite N à cette valeur (et probablement
bien en deçà) et donc  ce qui donne une probabilité non
négligeable d'être seul. Je peux cependant me demander quelle valeur je
dois accorder aux estimations des physiciens si je crois qu'ils ne sont
que des images mentales.
ce qui donne une probabilité non
négligeable d'être seul. Je peux cependant me demander quelle valeur je
dois accorder aux estimations des physiciens si je crois qu'ils ne sont
que des images mentales.
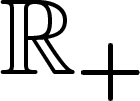 , ce qui n'est guère plus
possible que sur
, ce qui n'est guère plus
possible que sur 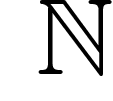 . Pour éviter cela, il suffit de la même manière de
borner la durée de vie de notre civilisation (par exemple par la mort du
Soleil dans 5 milliards d'années, ou par la durée que mettra notre espèce
à muter en une autre). Vu les intégrales à prendre en compte, cela ne
doit pas beaucoup modifier les résultats numériques (et d'ailleurs plutôt
à la hausse) dans les cas exponentiel et polynomial, et cela restitue une
valeur non nulle à la probabilité dans les cas où celle-ci était nulle
(et dans ce cadre, d'ailleurs, le contre-argument du report du contrôle
sur la génération suivante ne tient plus puisque le temps est borné).
. Pour éviter cela, il suffit de la même manière de
borner la durée de vie de notre civilisation (par exemple par la mort du
Soleil dans 5 milliards d'années, ou par la durée que mettra notre espèce
à muter en une autre). Vu les intégrales à prendre en compte, cela ne
doit pas beaucoup modifier les résultats numériques (et d'ailleurs plutôt
à la hausse) dans les cas exponentiel et polynomial, et cela restitue une
valeur non nulle à la probabilité dans les cas où celle-ci était nulle
(et dans ce cadre, d'ailleurs, le contre-argument du report du contrôle
sur la génération suivante ne tient plus puisque le temps est borné).
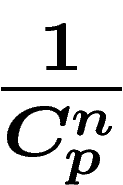 . La formule de Bayes donne alors, avec le même N que
précédemment (qui cette fois-ci ne tombe pas sous la critique de
l'inexistence des physiciens), que la probabilité que nous soyons seuls
dans l'univers est
. La formule de Bayes donne alors, avec le même N que
précédemment (qui cette fois-ci ne tombe pas sous la critique de
l'inexistence des physiciens), que la probabilité que nous soyons seuls
dans l'univers est ![\[ \frac{1}{\sum_{p=n}^N\frac1{C_p^n}} \]](extrater050.png)
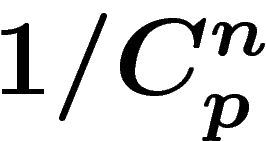 converge très vite pour
converge très vite pour
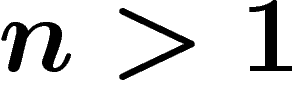 , est très proche de
, est très proche de 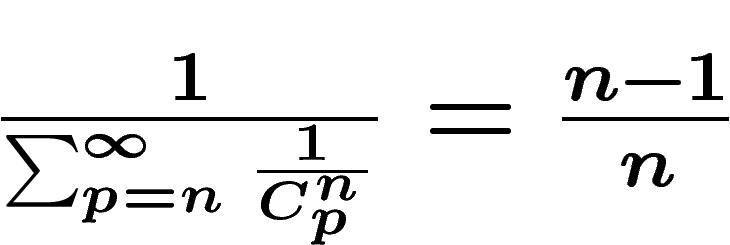 (voir en annexe une ébauche de preuve de
cette dernière égalité), ce qui laisse 1 chance sur n (n=5 milliards)
qu'il y ait des extraterrestres.
(voir en annexe une ébauche de preuve de
cette dernière égalité), ce qui laisse 1 chance sur n (n=5 milliards)
qu'il y ait des extraterrestres.
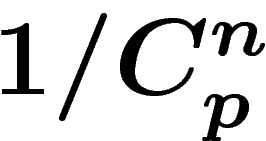 doit donc être revu à la hausse,
ce qui augmente la probabilité d'existence des extraterrestres.
doit donc être revu à la hausse,
ce qui augmente la probabilité d'existence des extraterrestres.
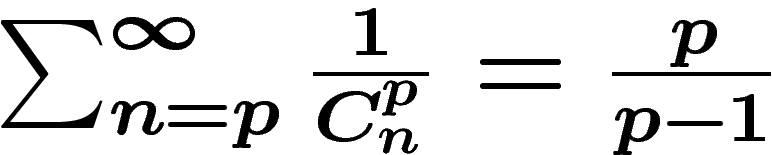 .
.
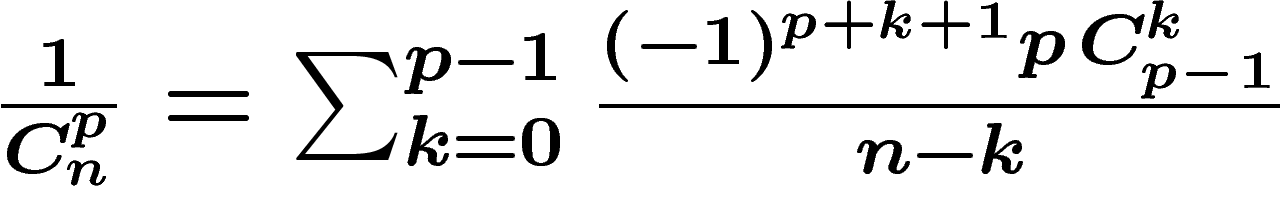 , ce
qui constitue une belle simplification dans la mesure où, ajoutant ces
quantités pour n variant de p à l'infini, on a des télescopages massifs
qui permettent de réduire l'expression
, ce
qui constitue une belle simplification dans la mesure où, ajoutant ces
quantités pour n variant de p à l'infini, on a des télescopages massifs
qui permettent de réduire l'expression 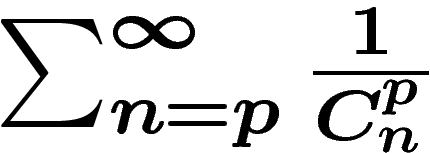 à disséquer à la valeur nettement
plus agréable
à disséquer à la valeur nettement
plus agréable
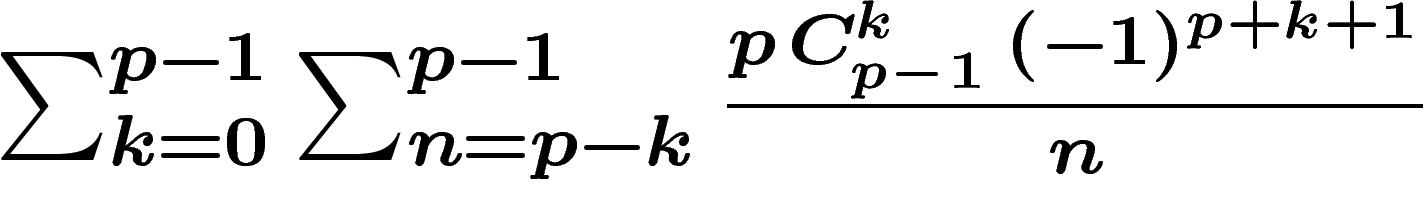 . Une partie de cette expression peut être calculée à
partir de la valeur d'une autre partie au rang précédent, ce qui donne
après moult calcul que cette expression vaut aussi
. Une partie de cette expression peut être calculée à
partir de la valeur d'une autre partie au rang précédent, ce qui donne
après moult calcul que cette expression vaut aussi
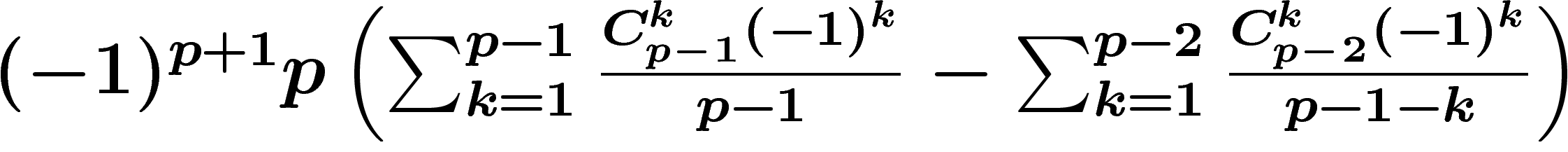 . Le premier terme se
simplifie immédiatement grâce à la formule du binôme. Le second nécessite
de séparer les cas pair et impair et d'utiliser des scissions puis
recoupements d'indices conjointement avec maintes propriétés des
coefficients binomiaux. Tout un programme.
. Le premier terme se
simplifie immédiatement grâce à la formule du binôme. Le second nécessite
de séparer les cas pair et impair et d'utiliser des scissions puis
recoupements d'indices conjointement avec maintes propriétés des
coefficients binomiaux. Tout un programme.