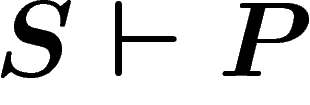 , si P est une
conséquence des axiomes de S.
, si P est une
conséquence des axiomes de S.
 dont les éléments satisfont les axiomes de S, ce que
l'on note
dont les éléments satisfont les axiomes de S, ce que
l'on note 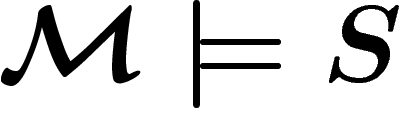 .
.
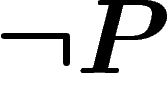 (la négation de P) ne sont des théorèmes de
S.
(la négation de P) ne sont des théorèmes de
S.
Je donne ici plusieurs manières précises d'énoncer le théorème d'incomplétude de Gödel, ainsi qu'une esquisse de démonstration. J'essaierai ensuite de traiter rigoureusement quelques interprétations couramment avancées de ce théorème.
Pour lire ce texte, il n'est pas nécessaire d'avoir une formation spécifique en logique mathématique.
Ce texte existe aussi au format ps gzippé et au format pdf.
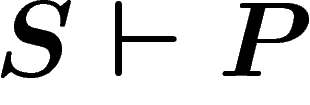 , si P est une
conséquence des axiomes de S.
, si P est une
conséquence des axiomes de S.
 dont les éléments satisfont les axiomes de S, ce que
l'on note
dont les éléments satisfont les axiomes de S, ce que
l'on note 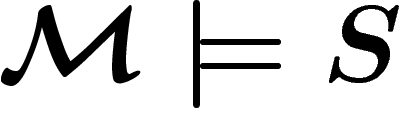 .
.
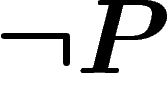 (la négation de P) ne sont des théorèmes de
S.
(la négation de P) ne sont des théorèmes de
S.
La première chose à noter est que l'indécidabilité n'a rien d'extraordinaire. Ainsi si l'on prend pour S les axiomes d'un groupe, la proposition qui exprime que le groupe n'a que trois éléments est indécidable, simplement parce qu'il existe des groupes à trois éléments et des groupes à plus de trois éléments ; autrement dit le système possède plusieurs modèles différents.
Plus précisément, un théorème de complétude de Gödel (qui malheureusement reçoit moins de publicité que son théorème d'incomplétude) précise que si une proposition est indécidable, alors il existe un modèle où elle est vraie et un modèle où elle est fausse. Autrement dit : si une proposition est vraie dans le système formel S (par vraie on entend vérifiée dans tous les modèles de S), alors elle est démontrable dans S (c'est-à-dire qu'il existe une suite de déductions formelles à partir des axiomes de S qui la démontre).
Un énoncé du théorème de Gödel est le suivant : pour tout système formel S contenant le langage de l'arithmétique, il existe une proposition G indémontrable dans S (sauf si S est contradictoire, auquel cas il démontre n'importe quoi).
Il y a une restriction supplémentaire : le système doit être récursif, c'est-à-dire, en gros, qu'on doit pouvoir reconnaître les axiomes par un programme.
Je ne détaillerai pas ce que signifie « contenant le langage de l'arithmétique ». Par simplicité, on prendra par la suite, et définitivement, pour S la théorie usuelle des ensembles.
L'idée maîtresse de la construction de Gödel est la suivante : il est tout à fait possible d'exprimer dans S ce qu'est la logique mathématique, ce qu'est une déduction, ce qu'est un modèle, etc. Partant, il est possible, dans le langage de S, d'exprimer une phrase qui dit « telle proposition est démontrable à partir de tels axiomes ».
Comment faire cela ? Rappelons que pour S nous prenons, par souci de simplicité, la théorie des ensembles usuelle. Il suffit alors de donner, dans S, des définitions de ce qu'est une suite de symboles, puis une suite de symboles syntaxiquement correcte (une proposition), de ce qu'est une déduction logique formelle (propriété d'une suite de propositions telle que chaque proposition découle des précédentes par applications d'une manipulation formelle correspondant à une déduction logique).
Par conséquent, comme S est assez puissant pour exprimer toute
manipulation sur des suites de symboles, et qu'une preuve à partir
d'axiomes est justement une certaine manipulation de suites de
symboles, on peut parfaitement, pour tout système d'axiomes A
(fini), produire une formule 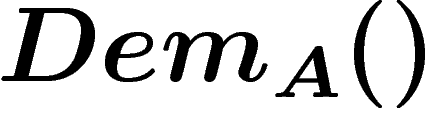 de S telle que
de S telle que 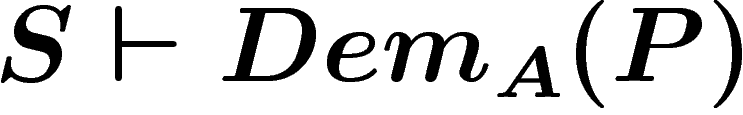 si et seulement si la proposition P du langage de A est
démontrable à partir des axiomes A. (Il n'est pas nécessaire que le
système d'axiomes A soit fini : il suffit qu'on puisse écrire une
formule finie, ou un programme, capable de dire pour toute chaîne de
symboles si oui ou non c'est un élément de A ; c'est le cas pour la
théorie des ensembles usuelle.)
si et seulement si la proposition P du langage de A est
démontrable à partir des axiomes A. (Il n'est pas nécessaire que le
système d'axiomes A soit fini : il suffit qu'on puisse écrire une
formule finie, ou un programme, capable de dire pour toute chaîne de
symboles si oui ou non c'est un élément de A ; c'est le cas pour la
théorie des ensembles usuelle.)
La formule 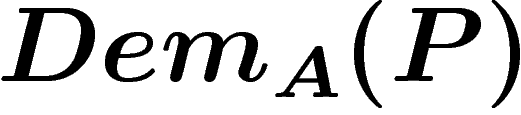 sera quelque chose comme : « il existe un entier
n (longueur de la démonstration) et une suite de n suites de
symboles (n propositions constituant la démonstration) telle que
chacune de ces suites de symboles est soit un axiome de A, soit est
obtenue par déduction de telle et telle manière à partir des
précédentes, et telle que la dernière suite de symboles est exactement
P ».
sera quelque chose comme : « il existe un entier
n (longueur de la démonstration) et une suite de n suites de
symboles (n propositions constituant la démonstration) telle que
chacune de ces suites de symboles est soit un axiome de A, soit est
obtenue par déduction de telle et telle manière à partir des
précédentes, et telle que la dernière suite de symboles est exactement
P ».
Remarquons bien le type des différents éléments : 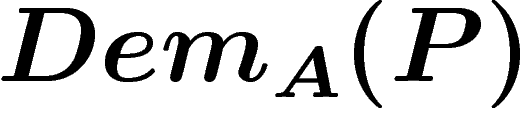 est une
formule du langage de S ; P est une proposition écrite dans le
langage que nous avons utilisé pour faire faire à S de la logique
(ce n'est pas une proposition de S), et A est un ensemble
d'axiomes exprimés dans ce même langage.
est une
formule du langage de S ; P est une proposition écrite dans le
langage que nous avons utilisé pour faire faire à S de la logique
(ce n'est pas une proposition de S), et A est un ensemble
d'axiomes exprimés dans ce même langage.
On notera désormais ces niveaux d'imbrication par différents niveaux
de guillemets : ainsi nous noterons sans guillemets (niveau 0) les
propositions qui sont exprimées dans notre langage naturel :
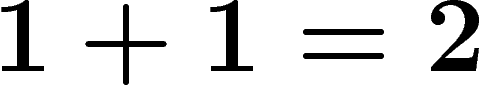 . Nous noterons avec des guillemets ``" (niveau 1) les
propositions et objets du système formel S :
. Nous noterons avec des guillemets ``" (niveau 1) les
propositions et objets du système formel S : 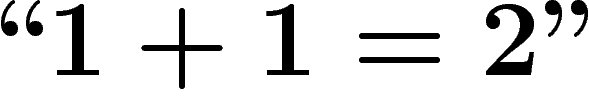 , que l'on
devrait en fait noter
, que l'on
devrait en fait noter  . Nous noterons
aussi S lui-même avec des guillemets. Nous savons, par exemple, que
. Nous noterons
aussi S lui-même avec des guillemets. Nous savons, par exemple, que
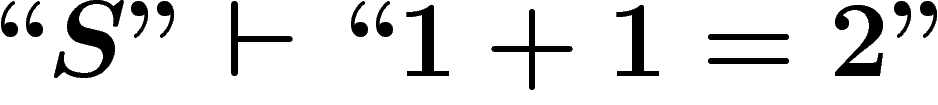 .
.
Enfin nous noterons avec des symboles  (niveau 2) les propositions et
objets écrits dans le langage symbolique que nous avons développé pour faire
faire de la logique à
(niveau 2) les propositions et
objets écrits dans le langage symbolique que nous avons développé pour faire
faire de la logique à  . Nous renoterons par
. Nous renoterons par  la proposition Dem ci-dessus, puisque c'est une proposition de
la proposition Dem ci-dessus, puisque c'est une proposition de
 qui ressemble à notre
qui ressemble à notre  .
.
Nous avons ainsi par exemple la formule suivante : 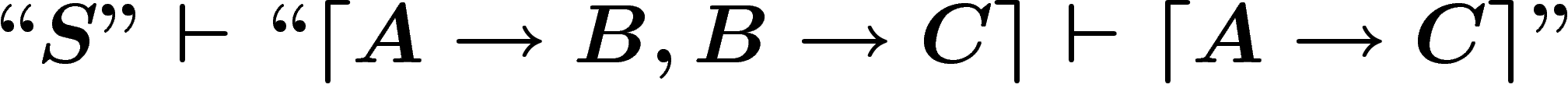 .
.
Tout cela pour éviter des erreurs d'interprétation courantes dues au
fait qu'on oublie qu'un système  ne peut pas parler
directement des formules de
ne peut pas parler
directement des formules de  . Autrement dit, une formule comme
. Autrement dit, une formule comme
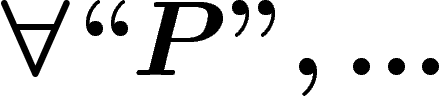 n'est pas une formule de niveau 1 (mais c'est une
formule de niveau 0). Mais
n'est pas une formule de niveau 1 (mais c'est une
formule de niveau 0). Mais  peut très bien parler directement
des formules de niveau 2 (c'est lui qui les a construites).
peut très bien parler directement
des formules de niveau 2 (c'est lui qui les a construites).
Maintenant, que signifie le fait que la formule  est bien
l'analogue dans
est bien
l'analogue dans  de la notion de démonstration ? Cela signifie que
notre procédé de construction de
de la notion de démonstration ? Cela signifie que
notre procédé de construction de  garantit des propriétés comme
garantit des propriétés comme
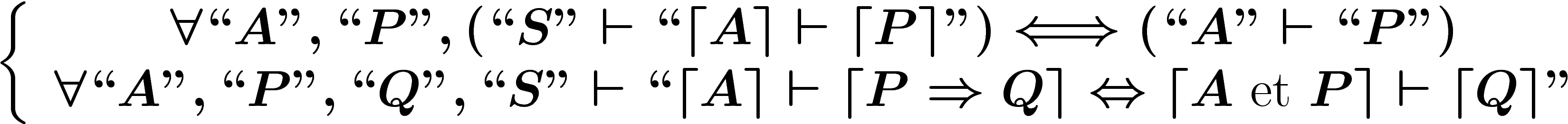
 . Pour la première par
exemple, à partir d'une démonstration symbolique du code de
. Pour la première par
exemple, à partir d'une démonstration symbolique du code de  à
partir du code des axiomes
à
partir du code des axiomes  , il me suffit simplement d'enlever
les guillemets
, il me suffit simplement d'enlever
les guillemets  pour obtenir une démonstration de
pour obtenir une démonstration de
 à partir de
à partir de  .
.
Attention cependant, ceci n'est vrai que sous certaines
hypothèses sur  : à savoir, que tous les axiomes composant
: à savoir, que tous les axiomes composant  soient vrais pour nous (sinon, on démontre n'importe quoi). Nous avons
pris pour
soient vrais pour nous (sinon, on démontre n'importe quoi). Nous avons
pris pour  la théorie des ensembles.
la théorie des ensembles.
L'idée de Gödel consiste à faire étudier à  le système
le système  ,
plus exactement à regarder
,
plus exactement à regarder 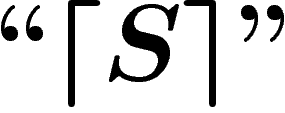 dans
dans  . Maintenant, on va,
par un procédé astucieux, fabriquer une formule G telle que G
soit équivalente à « S ne démontre pas G ». Plus précisément,
. Maintenant, on va,
par un procédé astucieux, fabriquer une formule G telle que G
soit équivalente à « S ne démontre pas G ». Plus précisément,
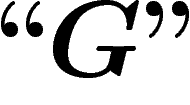 sera équivalente dans
sera équivalente dans  à la traduction de niveau 2 que ``
à la traduction de niveau 2 que ``
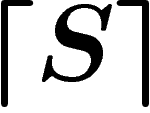 ne démontre pas
ne démontre pas 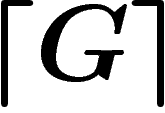 " :
" :
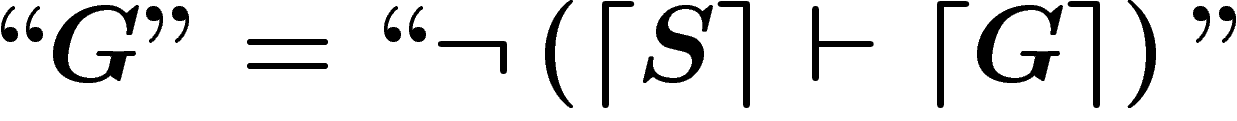
Cette phrase 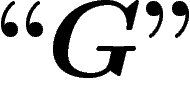 est une n-ième version du paraxode d'Épiménide («
tout les Crétois sont des menteurs », ou encore « cette phrase est
fausse »), qui a l'avantage de se prêter très bien à un traitement
rigoureux, et qui est formellement inattaquable.
est une n-ième version du paraxode d'Épiménide («
tout les Crétois sont des menteurs », ou encore « cette phrase est
fausse »), qui a l'avantage de se prêter très bien à un traitement
rigoureux, et qui est formellement inattaquable.
(Cette section plus technique peut être sautée en admettant
l'existence de 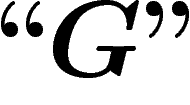 .)
.)
La construction de 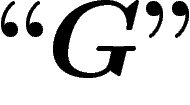 est comme suit. Remarquons d'abord qu'une
proposition de niveau 1 est un simple objet au niveau 0 (une suite de
symboles) ; de même une proposition au niveau 2 est en particulier un
objet de niveau 1. On note d'abord
est comme suit. Remarquons d'abord qu'une
proposition de niveau 1 est un simple objet au niveau 0 (une suite de
symboles) ; de même une proposition au niveau 2 est en particulier un
objet de niveau 1. On note d'abord
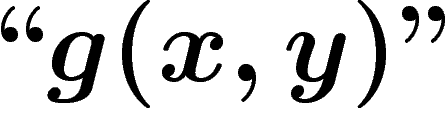 la fonction suivante, qui prend deux objets de niveau
1 et renvoie un objet de niveau 1 :
la fonction suivante, qui prend deux objets de niveau
1 et renvoie un objet de niveau 1 :
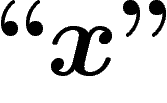 est un objet de niveau 1 qui est le code d'une
proposition de niveau 2 à une variable :
est un objet de niveau 1 qui est le code d'une
proposition de niveau 2 à une variable : 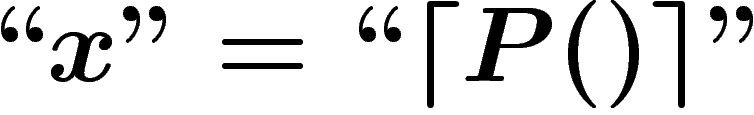 (
(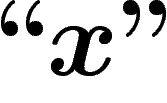 est une suite de symboles représentant une formule
syntaxiquement correcte). On pose alors
est une suite de symboles représentant une formule
syntaxiquement correcte). On pose alors 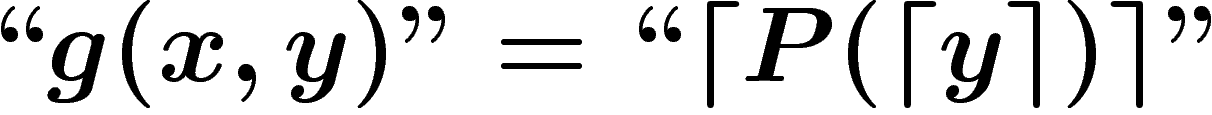 . À noter qu'alors,
. À noter qu'alors, 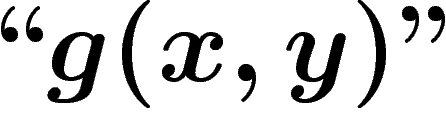 est aussi un objet de niveau 1
qui code une formule (sans variable libre) de niveau 2.
est aussi un objet de niveau 1
qui code une formule (sans variable libre) de niveau 2.
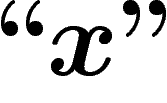 est un objet de niveau 1 qui n'est pas le code d'une
proposition de niveau 2 à une variable : on pose alors
est un objet de niveau 1 qui n'est pas le code d'une
proposition de niveau 2 à une variable : on pose alors
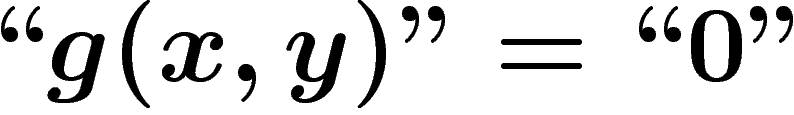 (le ``0" de
(le ``0" de  ).
).
Il faut aussi ajouter à la définition de 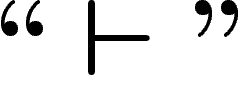 la convention que
la convention que 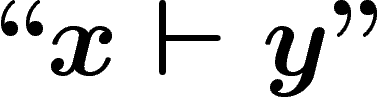 vaut ``faux" si
vaut ``faux" si 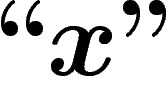 et
et 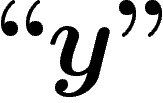 ne sont pas des symboles de
niveau 1 codant des formules de niveau 2.
ne sont pas des symboles de
niveau 1 codant des formules de niveau 2.
Ensuite, notons 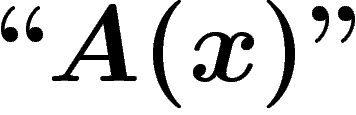 la formule
la formule 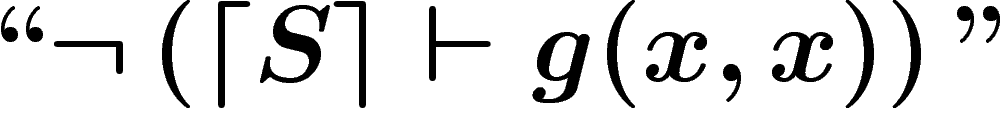 .
. 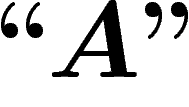 est une formule de
est une formule de  , donc on peut regarder son
code
, donc on peut regarder son
code 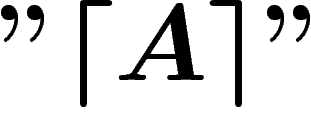 qui est une formule de niveau 2, donc un objet
de
qui est une formule de niveau 2, donc un objet
de  . Notons donc enfin
. Notons donc enfin 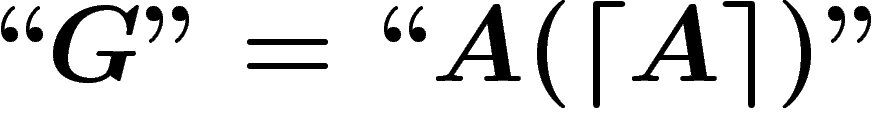 .
.
En redéveloppant les définitions, on voit que
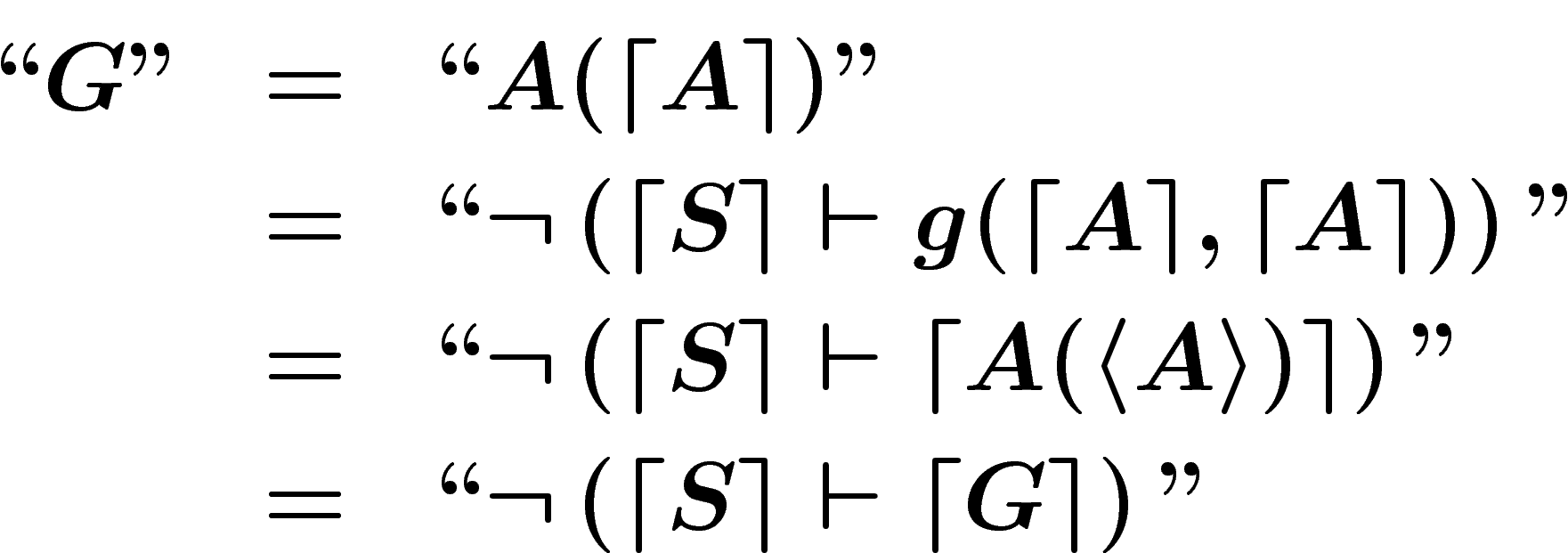
 pour indiquer un objet de niveau 3.
pour indiquer un objet de niveau 3.
Ce qui est bien la propriété annoncée.
L'existence de  a des conséquences immédiates très simples.
a des conséquences immédiates très simples.
En particulier,  n'est pas démontrable dans
n'est pas démontrable dans  (sauf si
(sauf si
 est contradictoire). En effet, supposons que
est contradictoire). En effet, supposons que 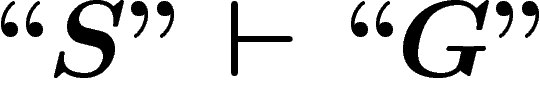 . Alors, d'après notre construction de
. Alors, d'après notre construction de  , on a
, on a 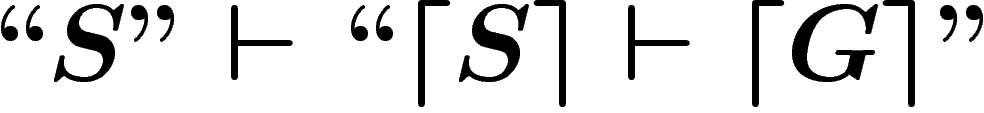 . Mais par la définition de
. Mais par la définition de 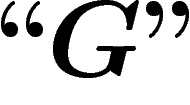 , dire que
, dire que 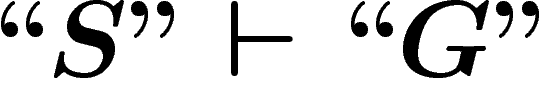 revient à dire justement, que
revient à dire justement, que  ne démontre pas que
ne démontre pas que
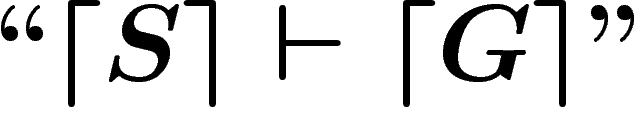 . Autrement dit, si
. Autrement dit, si 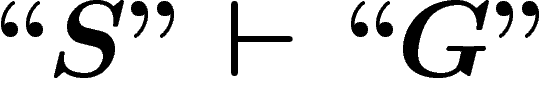 , alors
, alors  démontre le faux, et est contradictoire.
démontre le faux, et est contradictoire.
De la même manière, on prouve que 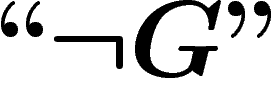 n'est pas non plus
démontrable dans
n'est pas non plus
démontrable dans  .
.
Une autre conséquence, qui constitue le second théorème d'incomplétude
de Gödel, est que  ne peut pas prouver la formule ``
ne peut pas prouver la formule ``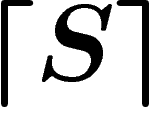 n'est pas contradictoire". La démonstration est la suivante :
si
n'est pas contradictoire". La démonstration est la suivante :
si  prouvait que
prouvait que 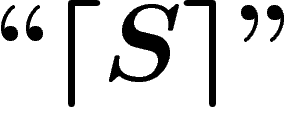 n'est pas contradictoire,
alors
n'est pas contradictoire,
alors  pourrait refaire, un niveau en-dessous, le raisonnement
que nous venons d'écrire ci-dessus (où nous avons utilisé la
non-contradiction de
pourrait refaire, un niveau en-dessous, le raisonnement
que nous venons d'écrire ci-dessus (où nous avons utilisé la
non-contradiction de  ), et prouver que
), et prouver que 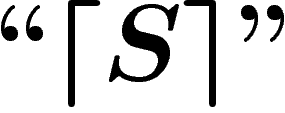 est soumis
au théorème de Gödel ; autrement dit,
est soumis
au théorème de Gödel ; autrement dit,  prouverait que
prouverait que 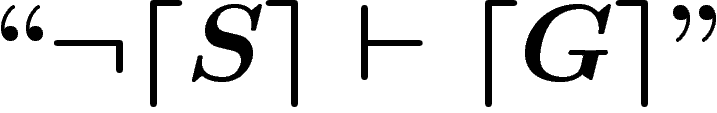 ... mais ceci est précisément
la phrase de Gödel, dont nous venons de prouver qu'elle n'était pas
prouvable dans
... mais ceci est précisément
la phrase de Gödel, dont nous venons de prouver qu'elle n'était pas
prouvable dans  , si
, si  était non-contradictoire.
était non-contradictoire.
Pour la première affirmation, non : si la phrase  de Gödel était vraie
(i.e. vérifiée dans tout modèle de
de Gödel était vraie
(i.e. vérifiée dans tout modèle de  ), alors elle serait
démontrable, en vertu, précisément, du théorème de complétude
du même Gödel. Il y a donc des modèles de
), alors elle serait
démontrable, en vertu, précisément, du théorème de complétude
du même Gödel. Il y a donc des modèles de  où
où  est fausse.
est fausse.
Cette croyance est suggérée par l'interprétation courante de  : « le
système
: « le
système  ne peut pas prouver
ne peut pas prouver  », ce qu'on a précisément
prouvé. Or
», ce qu'on a précisément
prouvé. Or 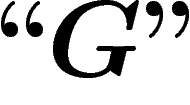 dit plutôt ``le système
dit plutôt ``le système 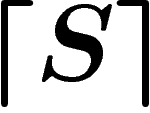 ne peut
pas prouver
ne peut
pas prouver 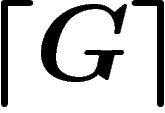 ". Quand on pense « le
système
". Quand on pense « le
système  ne peut pas prouver
ne peut pas prouver 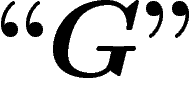 », on a affaire à une autre
proposition, appelons-la G, et que l'on a bel et bien prouvée. Plus
exactement on a prouvé que ou bien G était vraie ou bien
», on a affaire à une autre
proposition, appelons-la G, et que l'on a bel et bien prouvée. Plus
exactement on a prouvé que ou bien G était vraie ou bien  était contradictoire. Évidemment,
était contradictoire. Évidemment, 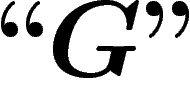 est la traductionn de G
dans
est la traductionn de G
dans  , mais ce qu'on attendrait que
, mais ce qu'on attendrait que  prouve, s'il est
aussi doué que nous, devrait être
non pas
prouve, s'il est
aussi doué que nous, devrait être
non pas 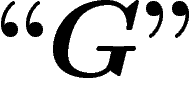 mais ``G ou
mais ``G ou 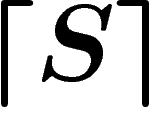 est contradictoire" ;
et, précisément, cette phrase est prouvable dans
est contradictoire" ;
et, précisément, cette phrase est prouvable dans  (i.e. en
utilisant la non-contradiction de
(i.e. en
utilisant la non-contradiction de 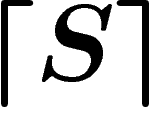 , que
, que  ne
pouvait justement pas prouver,
ne
pouvait justement pas prouver,  peut arriver à prouver
peut arriver à prouver 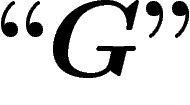 ).
).
Ce qui est implicite dans le sentiment que l'intuition humaine dépasse
les systèmes formels est le fait que nous-mêmes avons l'impression de
travailler dans un système de raisonnement qui est la théorie des
ensembles (en général), et qu'on a choisi le système  précisément pour coller à notre propre intuition :
précisément pour coller à notre propre intuition :  est un
candidat à notre formalisation. Par conséquent,
nous avons réussi à prouver G alors que
est un
candidat à notre formalisation. Par conséquent,
nous avons réussi à prouver G alors que  ne peut pas
prouver
ne peut pas
prouver 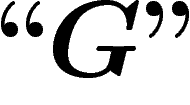 , d'où l'impression que l'intuition humaine n'est
capturable par aucun système formel (la démonstration de Gödel
s'applique à tout système formel assez puissant pour exprimer
l'arithmétique, pas seulement à la théorie des ensembles).
, d'où l'impression que l'intuition humaine n'est
capturable par aucun système formel (la démonstration de Gödel
s'applique à tout système formel assez puissant pour exprimer
l'arithmétique, pas seulement à la théorie des ensembles).
Mais nous n'avons prouvé G que si  n'est pas contradictoire,
ce dont nous ne savons rien pour le moment... Peut-être pouvons-nous
le prouver.
n'est pas contradictoire,
ce dont nous ne savons rien pour le moment... Peut-être pouvons-nous
le prouver.
Avant de raisonner sur ce que nous pourrions prouver, constatons que
nous n'avons pas le droit de raisonner directement sur nos propres
propositions et formules ; nous ne pouvons simplement pas dire « je
peux prouver telle formule », nous ne pouvons pas écrire 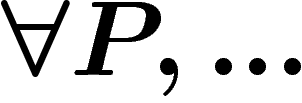 , de la même manière que
, de la même manière que  ne peut pas écrire
ne peut pas écrire 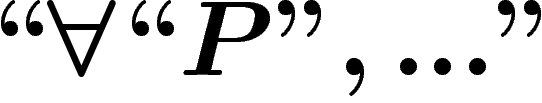 . Par contre, nous pouvons fort bien écrire
. Par contre, nous pouvons fort bien écrire 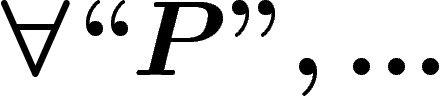 Pour pouvoir analyser les raisonnements que nous pouvons mener, il
convient justement de nous mettre à la place de
Pour pouvoir analyser les raisonnements que nous pouvons mener, il
convient justement de nous mettre à la place de  , et, bien sûr, de
remplacer
, et, bien sûr, de
remplacer  par
par 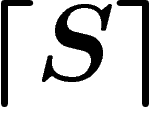 .
.
Supposons donc un instant que nous soyons un système formel  et
regardons-le. On sait que si
et
regardons-le. On sait que si  admet que
admet que 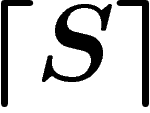 n'est
pas contradictoire, alors
n'est
pas contradictoire, alors  peut prouver
peut prouver 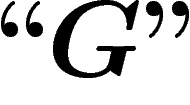 (ce que nous
faisons depuis le début). Mais justement
(ce que nous
faisons depuis le début). Mais justement  ne peut pas prouver
que
ne peut pas prouver
que 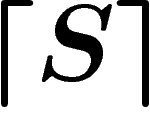 n'est pas contradictoire... à moins que lui-même
soit contradictoire. Donc, si nous sommes un système formel S, à
moins d'être nous-mêmes contradictoires, nous ne pourrons pas prouver
que
n'est pas contradictoire... à moins que lui-même
soit contradictoire. Donc, si nous sommes un système formel S, à
moins d'être nous-mêmes contradictoires, nous ne pourrons pas prouver
que  n'est pas contradictoire, et nous pouvons prouver seulement
que « G ou
n'est pas contradictoire, et nous pouvons prouver seulement
que « G ou  est contradictoire » : nous ne faisons pas mieux
que
est contradictoire » : nous ne faisons pas mieux
que  (forcément, si nous sommes un système formel). Nous ne
pouvons même pas prouver que nous ne sommes pas contradictoires (sauf
si nous sommes contradictoires). Et nous ne pouvons même pas prouver
que nous ne pouvons pas prouver que nous ne sommes pas contradictoires
(sauf si nous sommes contradictoires). Etc.
(forcément, si nous sommes un système formel). Nous ne
pouvons même pas prouver que nous ne sommes pas contradictoires (sauf
si nous sommes contradictoires). Et nous ne pouvons même pas prouver
que nous ne pouvons pas prouver que nous ne sommes pas contradictoires
(sauf si nous sommes contradictoires). Etc.
Continuons à discuter l'affirmation « l'intuition humaine n'est pas formalisable ».
Justement, nous avons l'impression que nous, nous nous rendons
compte des moments où nous rencontrons une phrase de type Gödel, et où
pour continuer il faut supposer que nous ne sommes pas
contradictoires. Eh bien, dans tout système S, on peut ajouter la
connaissance que  est non contradictoire, connaissance que S
pourra utiliser pour démontrer, par exemple, des phrases de Gödel
portant sur
est non contradictoire, connaissance que S
pourra utiliser pour démontrer, par exemple, des phrases de Gödel
portant sur  . Mais ce faisant, par ajout d'un axiome, on a
obtenu un système différent
. Mais ce faisant, par ajout d'un axiome, on a
obtenu un système différent 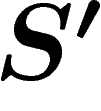 , qui peut bien parler de la
gödelisation de
, qui peut bien parler de la
gödelisation de  , mais pas de celle de
, mais pas de celle de 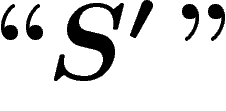 . Pour que
. Pour que
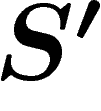 puisse parler de sa gödelisation, il faudrait lui ajouter la
non-contradiction de
puisse parler de sa gödelisation, il faudrait lui ajouter la
non-contradiction de 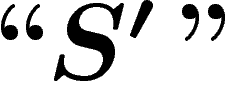 , obtenant ainsi un second système
, obtenant ainsi un second système
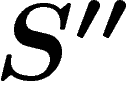 , etc. Il se peut fort bien que nous autres soyons modélisés par
un système obtenu par un grand nombre d'itérations de ce processus, et
que nous ayons ainsi l'impression d'être un système S qui peut
parler de la gödelisation de
, etc. Il se peut fort bien que nous autres soyons modélisés par
un système obtenu par un grand nombre d'itérations de ce processus, et
que nous ayons ainsi l'impression d'être un système S qui peut
parler de la gödelisation de  , alors que ce n'est vrai qu'à un
grand ordre. Ceci peut expliquer notre impression que nous réussissons
face à Gödel là où les systèmes formels échouent.
, alors que ce n'est vrai qu'à un
grand ordre. Ceci peut expliquer notre impression que nous réussissons
face à Gödel là où les systèmes formels échouent.
Note pour les logiciens.
L'ordre auquel cette construction devrait
être itérée est au moins 1 pour toute personne connaissant le théorème
de Gödel. Il peut tout à fait être égal à un ordinal infini ; cela
devrait être le cas pour toute personne ayant lu ce texte. Mais si cet
ordre est égal à un certain ordinal  , on peut gödeliser à
l'ordre
, on peut gödeliser à
l'ordre 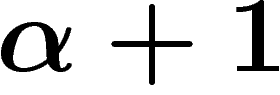 pourvu que la réunion du système de départ et de
toutes ses gödelisations jusqu'à l'ordre
pourvu que la réunion du système de départ et de
toutes ses gödelisations jusqu'à l'ordre  soit un système
d'axiomes récursif.
soit un système
d'axiomes récursif.
Il existe un plus petit ordinal 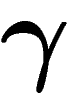 où ce n'est plus le cas ; j'ignore
quel il est (il est inférieur ou égal au plus petit ordinal non
démonbrable pour des raisons évidentes de cardinalité).
où ce n'est plus le cas ; j'ignore
quel il est (il est inférieur ou égal au plus petit ordinal non
démonbrable pour des raisons évidentes de cardinalité).
Ceci est sans doute en rapport avec le fait qu'on ne peut pas nommer
algorithmiquement tous les ordinaux dénombrables ; sinon, peut-être
que cela pourrait permettre de reconnaître si une proposition donnée
est une proposition de Gödel à un certain ordre. En tout cas, le
théorème de Gödel prouve justement que l'ensemble des phrases de Gödel
pour les ordinaux inférieurs à 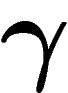 n'est pas calculable.
n'est pas calculable.
Ces quelques niveaux de non-contradiction que nous nous accordons à nous-mêmes, nous les devons sans doute à la sélection naturelle ou à notre orgueil.
Il semble pourtant que, si  n'est pas contradictoire, la
non-contradiction de
n'est pas contradictoire, la
non-contradiction de 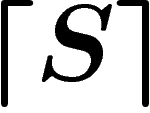 est ``vraie", puisque cela
signifie la même chose ; auquel cas
est ``vraie", puisque cela
signifie la même chose ; auquel cas 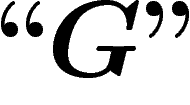 serait ``vraie" pour
serait ``vraie" pour
 . Mais cela repose sur notre assimilation implicite de «
. Mais cela repose sur notre assimilation implicite de «  n'est pas contradictoire » et ``
n'est pas contradictoire » et ``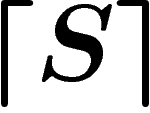 n'est pas
contradictoire", ou plus précisément sur notre assimilation de
n'est pas
contradictoire", ou plus précisément sur notre assimilation de
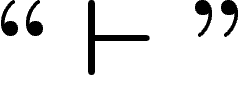 et
et 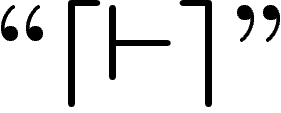 . On a bien nos formules de
consistance ref{eq:cons}, mais c'est insuffisant : dans un certain
modèle de
. On a bien nos formules de
consistance ref{eq:cons}, mais c'est insuffisant : dans un certain
modèle de  , ``
, ``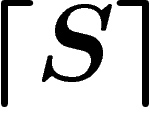 n'est pas contradictoire" est bel
et bien fausse.
n'est pas contradictoire" est bel
et bien fausse.
Comment se fait-ce ? Il existe des modèles non-standard de  , des
modèles, par exemple, où certains entiers sont considérés comme
arbitrairement grands. Dans ces modèles,
, des
modèles, par exemple, où certains entiers sont considérés comme
arbitrairement grands. Dans ces modèles, 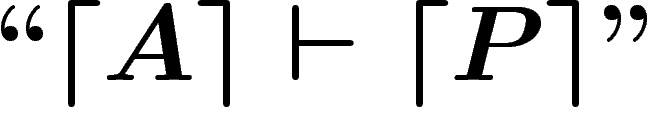 signifiera donc quelque chose comme : `` il existe
une démonstration, éventuellement de longueur non standard, utilisant
éventuellement des propositions de longueur non standard, de
signifiera donc quelque chose comme : `` il existe
une démonstration, éventuellement de longueur non standard, utilisant
éventuellement des propositions de longueur non standard, de 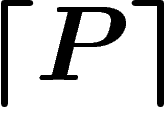 à partir de
à partir de 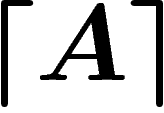 ". Ce n'est pas tout à fait la
notion intuitive de démonstration que nous avons... L'assimilation
entre
". Ce n'est pas tout à fait la
notion intuitive de démonstration que nous avons... L'assimilation
entre 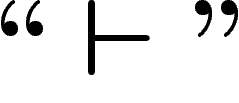 et
et 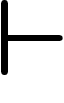 , entre G et
, entre G et 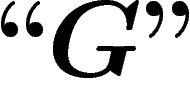 , qui nous donne
l'impression que puisque G est vraie, alors
, qui nous donne
l'impression que puisque G est vraie, alors 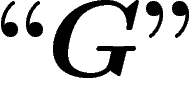 devrait être
vraie bien qu'indémontrable, n'est valable que dans certains modèles
de
devrait être
vraie bien qu'indémontrable, n'est valable que dans certains modèles
de  .
.
En ce sens, on peut avoir l'impression que c'est  qui
capture mal notre intuition des entiers ou des ensembles. En tout état
de cause, le théorème de Gödel prouve définitivement que tout système
formel assez puissant (pour exprimer l'arithmétique) comporte deux
modèles différents.
qui
capture mal notre intuition des entiers ou des ensembles. En tout état
de cause, le théorème de Gödel prouve définitivement que tout système
formel assez puissant (pour exprimer l'arithmétique) comporte deux
modèles différents.
Si nous croyons que nous avons en tête un modèle intuitif unique, il
ne peut donc pas être formalisé. Mais jusqu'ici, nous avons simplement
vu que notre intuition comprend, outre les propriétés habituelles
d'entiers et d'ensembles, quelques propositions de Gödel itérées à un
certain ordre, qui nous font dire que pour les entiers intuitifs, il y
a correspondance entre 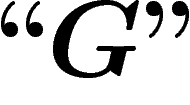 et
et 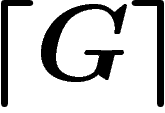 . Notre modèle
intuitif est non pas la version naïve des propriétés des entiers ou
des ensembles, mais la même chose avec en plus l'axiome que
. Notre modèle
intuitif est non pas la version naïve des propriétés des entiers ou
des ensembles, mais la même chose avec en plus l'axiome que 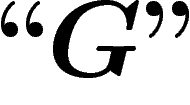 est
vraie ; et aussi que la phrase de Gödel
est
vraie ; et aussi que la phrase de Gödel 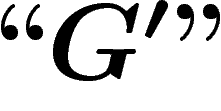 du système ainsi
obtenue est vraie, etc., ceci itéré jusqu'à un rang assez élevé, comme
ci-dessus, pour qu'on ne voie plus rien et qu'on ne puisse même plus
repérer si telle proposition est une proposition qui affirme une
vérité de Gödel. Notre modèle intuitif n'est pas unique, mais les
branchements se situent à un niveau de gödelisation itérée très élevé
(éventuellement égal à un ordinal infini). Et il est hors de portée
logique, hors de portée de notre entendement fini, de parler de
« tous » les niveaux de gödelisation.
du système ainsi
obtenue est vraie, etc., ceci itéré jusqu'à un rang assez élevé, comme
ci-dessus, pour qu'on ne voie plus rien et qu'on ne puisse même plus
repérer si telle proposition est une proposition qui affirme une
vérité de Gödel. Notre modèle intuitif n'est pas unique, mais les
branchements se situent à un niveau de gödelisation itérée très élevé
(éventuellement égal à un ordinal infini). Et il est hors de portée
logique, hors de portée de notre entendement fini, de parler de
« tous » les niveaux de gödelisation.
Un cas particulier de « modèle standard » : si pour  on prend
l'arithmétique, on sait, en effet, qu'en définissant
on prend
l'arithmétique, on sait, en effet, qu'en définissant 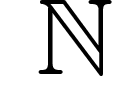 par la
théorie des ensembles, le modèle
par la
théorie des ensembles, le modèle 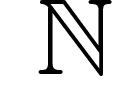 va vérifier le
va vérifier le 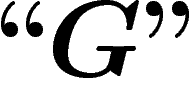 de
l'arithmétique. Cela veut simplement dire que la théorie des ensembles
est plus précise sur l'arithmétique que les axiomes usuels (de Peano)
que l'on prend pour les entiers, ce qui n'est pas une surprise (la
théorie des ensembles est plus forte, elle contient en particulier un
niveau au moins de gödelisation des entiers). Mais on ne sait pas
faire la même chose pour la théorie des ensembles, vu qu'on ne sait
pas en construire de modèle.
de
l'arithmétique. Cela veut simplement dire que la théorie des ensembles
est plus précise sur l'arithmétique que les axiomes usuels (de Peano)
que l'on prend pour les entiers, ce qui n'est pas une surprise (la
théorie des ensembles est plus forte, elle contient en particulier un
niveau au moins de gödelisation des entiers). Mais on ne sait pas
faire la même chose pour la théorie des ensembles, vu qu'on ne sait
pas en construire de modèle.
On peut aussi interpréter le « modèle standard » non pas comme celui qu'on a en tête sans jamais arriver à le décrire, mais comme celui du monde physique (en admettant qu'il y ait des nombres entiers « physiques » ou des ensembles « physiques »), de la réalité qui nous entoure. Dans ce cas, je ne vois pas quoi d'autre qu'un sentiment injustifié nous pousse à croire que G s'applique à celui-là. Alors, la phrase G serait une vérité indémontrable, mais elle porterait sur le monde physique, non sur une vérité logique accessible aux humains mais pas aux systèmes formels.
Ce n'est pas nouveau qu'il y a des propriétés de la réalité physique qui ne sont pas formellement démontrables : aucune ne l'est. Si nous utilisons tous les jours des propositions qui nous semblent vraies portant sur le monde extérieur, nous ne pouvons en fournir aucune démonstration rigoureuse ; mais nous possédons un grand nombre de connaissances sur le monde extérieur simplement par sélection naturelle, car le cerveau est conçu pour produire des résultats à peu près corrects sur la réalité qu'il doit traiter pour survivre.
Si donc 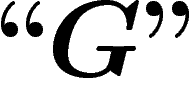 est ``vraie" en un certain sens, c'est en un sens
portant sur la réalité et non logiquement nécessaire. En tout cas rien
ne semble incompatible avec le fait qu'un être humain soit
intrinsèquement non formalisable.
est ``vraie" en un certain sens, c'est en un sens
portant sur la réalité et non logiquement nécessaire. En tout cas rien
ne semble incompatible avec le fait qu'un être humain soit
intrinsèquement non formalisable.
Non plus (ou du moins il faudra qu'on m'explique plus en détail).
Une traduction de la phrase de Gödel est « Untel ne peut pas prouver cette phrase sans se contredire ». Évidemment, Untel, voyant cette phrase, voit qu'elle est vraie --- et qu'il ne peut pas le prouver. Pourquoi ne peut-il pas le prouver, simplement en disant « quel que soit le système S, S ne peut pas prouver cette phrase sans se contredire. Par conséquent, si je suis un système formel, je ne peux pas prouver cette phrase sans me contredire » ? Il peut le dire, mais cela dépend de l'hypothèse « je suis un système formel » --- et alors il se contredit.
Nous avons donc bien prouvé --- et c'est une vraie conséquence du théorème de Gödel --- que je ne peux pas prouver que je suis un système formel ; ce qui ne veut pas dire que je n'en suis pas un (cela fera une vérité physique, et non logique, qui sera indémontrable) ; la situation est la même que pour notre non-contradiction.
De toute façon, la comparaison est assez mal choisie, puisqu'en fait,
les tenants de la thèse de l'intelligence artificielle forte (en gros,
un homme est une machine à neurones) ne veulent pas comparer un homme
à un système formel, mais plutôt à un automate fini : personne n'a
prétendu qu'un humain était un système formel. Un humain est un objet
qui à chaque instant se trouve dans un état mental ou dans un autre,
pas un objet qui a des axiomes vrais et qui démontre des théorèmes ;
il n'explose pas s'il prononce deux phrases contradictoires, il se
contente d'être dans tel ou tel état mental. Quand il voit un objet,
il ne demande pas de preuve que cet objet est tel ; ce qu'il voit
rappelle à son esprit les caractéristiques de l'objet ; ainsi pour G
et 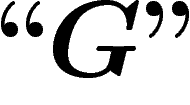 . Les réflexions sur les limitations des systèmes formels
sont donc à côté de la question.
. Les réflexions sur les limitations des systèmes formels
sont donc à côté de la question.
Bien sûr certains comportements de cet automate consistent à prendre pour vrais dans la réalité les résultats qu'il obtient quand il choisit de simuler un certain système formel ; mais cette croyance est sans démonstration (on ne démontre rien rigoureusement sur la réalité extérieure).
Pourquoi ces automates ont-ils intégré de telles croyances ? Par sélection naturelle. La capacité d'un animal à croire qu'il est un système formel obéissant à certaines règles permet de déduire des choses sur lui-même et est certainement un pas important vers la conscience.
Discutons maintenant, à la lumière de tout cela, le paradoxe classique du plus petit nombre qui ne peut pas être défini par moins de dix-neuf mots en français (et que nous venons de définir, en français, par dix-huit mots).
Appelons donc S « le français ». Construisons une expression de S
considérant les nombres que peut définir  : «
: « 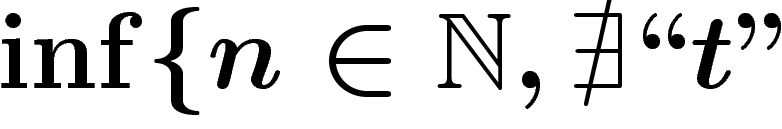 terme de
terme de  de longueur
de longueur 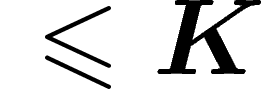 , tel que
, tel que
 prouve que
prouve que 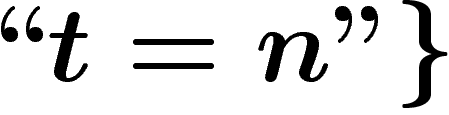 », expression dans laquelle K est bien sûr à
remplacer par la longueur de cette même expression (qui, dans le
détail, dépend en particulier de la manière dont on a défini
», expression dans laquelle K est bien sûr à
remplacer par la longueur de cette même expression (qui, dans le
détail, dépend en particulier de la manière dont on a défini  ,
dont on a construit les guillemets, dont on a exprimé
,
dont on a construit les guillemets, dont on a exprimé  etc.).
etc.).
Maintenant, le raisonnement courant est : si cette expression avait
pour valeur m dans S, cela serait évidemment contradictoire parce
que dans S, m serait défini par moins de K mots, tandis que par
définition sa définition aurait plus de K mots dans  . Or nous
(qui étudions S étudiant
. Or nous
(qui étudions S étudiant  ) savons de manière correcte que les
deux doivent être les mêmes...
) savons de manière correcte que les
deux doivent être les mêmes...
Effectivement, pour nous, S et  vont prouver les mêmes choses,
mais il peut exister plusieurs modèles de S dans laquelle la valeur
de m est différente, auquel cas il n'y aurait pas de preuve du
tout... Si un modèle étudie un modèle différent, il n'y a donc pas de
problème.
vont prouver les mêmes choses,
mais il peut exister plusieurs modèles de S dans laquelle la valeur
de m est différente, auquel cas il n'y aurait pas de preuve du
tout... Si un modèle étudie un modèle différent, il n'y a donc pas de
problème.
Le raisonnement « paradoxal » habituel prouve donc vraiment quelque chose : à savoir, que la valeur de m n'est pas décidable dans S, et qu'il existe des modèles où elle peut prendre des valeurs différentes (je ne sais pas lesquelles sont possibles). En effet, si la valeur de m était identique dans tous les modèles, alors S prouverait cette valeur, et donc le paradoxe s'appliquerait.
Encore une fois, cela ne prouve pas une quelconque « supériorité » du français sur S : S, de même que le français, s'aperçoit qu'il y a problème puisqu'il ne peut rien prouver. (Et on a vu que, de la même manière que le français peut dire « défini en français », S peut très bien dire ``défini dans S".)
L'on voit sur cet exemple que l'indécidabilité est là justement parce que l'interprétation de la proposition indécidable soulève un paradoxe.
Il en va de même de la phrase de Gödel ; si l'on suit précisément la construction, cette phrase est : « ``est indémontrable si précédée d'elle-même entre guillemets" est indémontrable si précédée d'elle-même entre guillemets ». Soit exactement « cette phrase est indémontrable », phrase face à laquelle le lecteur doit d'abord constater qu'elle ne peut pas être fausse... bien qu'il ne puisse pas la démontrer ! Où l'on rejoint le « cette phrase est fausse ».
L'indécidabilité de la phrase de Gödel, ainsi que de la valeur du plus petit nombre dont la définition..., sont donc heureuses : au contraire, si S arrivait à démontrer une valeur de vérité précise pour « cette phrase est fausse », cela serait inquiétant ! Un système formel, en cette circonstance, réagit donc exactement de la manière attendue : quand on lui demande de démontrer un paradoxe, il n'y arrive pas, et c'est heureux.
Avec cette interprétation, l'on voit combien il est aberrant de dire que la phrase de Gödel est une « vérité inconnaissable »...