Back to: Main Page > Mathématiques
Introduction à quelques propriétés des algorithmes génétiques
Yann Ollivier, octobre 2000
Aussi au format pdf ou postscript gzippé
Je décris ici diverses recherches amorcées dans le cadre du groupe de
travail organisé par R. Cerf sur les algorithmes génétiques, ainsi que la
manière dont j'envisage d'appliquer certaines de ces techniques à un
problème de théorie algorithmique des groupes, la génération d'un élément
aléatoire uniformément distribué dans un groupe fini (très grand).
Introduction aux algorithmes génétiques.
On cherche à trouver
une bonne solution à un certain problème, c'est-à-dire, en pratique, à
maximiser ou presque une fonction f sur un certain espace discret. On
ne veut pas adopter la solution qui consiste à explorer successivement
tous les points de l'espace. L'idée est de prendre un ensemble de
solutions plus ou moins bonnes, et d'appliquer des transformations sur
ces solutions afin de les améliorer. En répétant ces transformations, on
espère aboutir près d'un optimum (au moins local). On applique de plus
une méthode de sélection qui consiste évidemment à conserver les
meilleures solutions trouvées.
Les transformations utilisées s'inspirent de la biologie (d'où le nom) : elles
consistent en la mutation (transformation légère d'un individu donnant un
autre individu), le croisement (combinaison de deux individus) et la
sélection (la probabilité d'être parent d'un individu de la génération
suivante croît selon les performances de l'individu pour le problème de
départ).
On prend pour espace de recherche l'espace 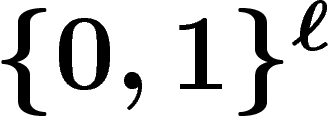 (on code les solutions du
problème par des suites de 0 et de 1). La mutation consiste alors à
changer probabilistement un petit nombre de bits (généralement, on change
chaque bit aléatoirement, indépendamment des autres, avec une probabilité
de l'ordre de
(on code les solutions du
problème par des suites de 0 et de 1). La mutation consiste alors à
changer probabilistement un petit nombre de bits (généralement, on change
chaque bit aléatoirement, indépendamment des autres, avec une probabilité
de l'ordre de 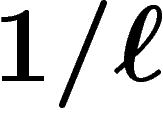 ).
).
Le croisement consiste à prendre pour chaque bit de
l'enfant l'un des deux bits des parents, et plusieurs méthodes sont
possibles pour cela : on peut, par exemple, décider de prendre les bits
d'un parent jusqu'à une certaine position, puis ceux de l'autre parent
(ce qui revient à couper le génome en un seul point) ;
on peut aussi simplement décider pour chaque bit avec probabilité 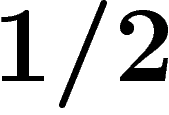 ,
indépendamment, si on prendra celui de l'un ou l'autre parent. Par la
suite, pour la simplicité de l'exposé, on se tiendra à cette dernière
possibilité.
,
indépendamment, si on prendra celui de l'un ou l'autre parent. Par la
suite, pour la simplicité de l'exposé, on se tiendra à cette dernière
possibilité.
Un algorithme génétique peut donc être décrit ainsi :
- choisir un codage des solutions par
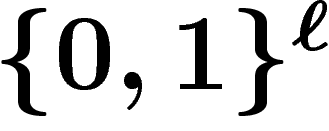 ; choisir une taille de
population k ; définir la fonction
; choisir une taille de
population k ; définir la fonction 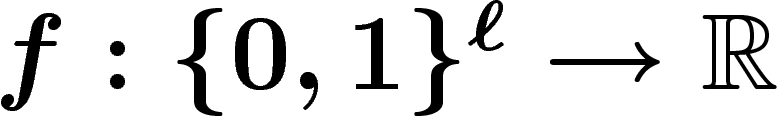 à optimiser ;
à optimiser ;
- prendre un k-uplet
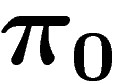 d'éléments de
d'éléments de 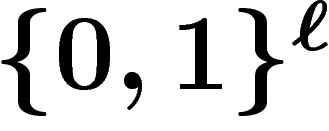 quelconques ;
quelconques ;
- définir récursivement un k-uplet aléatoire
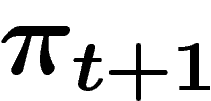 à partir
de
à partir
de 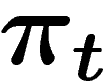 en répétant k fois de suite indépendamment les opérations
suivantes :
en répétant k fois de suite indépendamment les opérations
suivantes :
- tirer deux individus dans la population
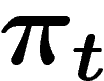 avec une
probabilité proportionnelle à la valeur de f sur ces individus,
avec une
probabilité proportionnelle à la valeur de f sur ces individus,
- croiser les deux individus tirés pour en obtenir un nouveau,
- muter le nouvel individu obtenu et le placer dans
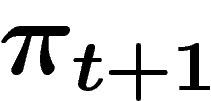 ;
;
- répéter ces opérations jusqu'à la fin des temps ou jusqu'à la
découverte d'une solution satisfaisante.
De très nombreuses variantes existent ; nous ne nous y intéresserons pas
ici.
Bien que les algorithmes génétiques se révèlent très efficaces en
pratique sur un grand nombre de problèmes, l'analyse théorique est
terriblement difficile et pratiquement inexistante, sauf dans des cas
très simples (fonction f linéaire --- auquel cas l'usage d'un
algorithme génétique pour l'optimiser sur 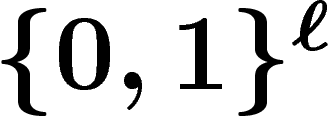 est incongru).
est incongru).
Étude de l'opérateur de croisement à population infinie.
Pour
aborder une étude théorique, Y. Rabani, Y. Rabinovich et A. Sinclair ont commencé par étudier l'opérateur
de croisement seul (voir [RRS]). On élimine donc la mutation, et on
évacue la fonction f à optimiser.
On entend souvent dire, en biologie, que l'intérêt de la reproduction
sexuée est de brasser l'information génétique efficacement, et de
maintenir une diversité supérieure à ce qu'elle serait par simple
mutation. Ces auteurs ont donc voulu évaluer si, et à quelle vitesse, le
croisement mélange l'information génétique.
Le plus simple est d'étudier la situation où la taille de la population
k est infinie : on se retrouve alors à manipuler des lois de
probabilité sur 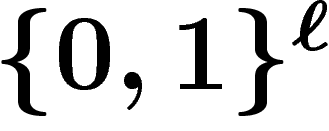 , l'évolution de ces lois étant déterministe. Si
, l'évolution de ces lois étant déterministe. Si
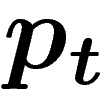 désigne la loi de probabilité obtenue sur
désigne la loi de probabilité obtenue sur 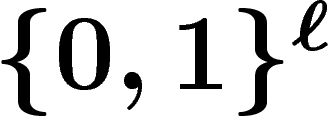 au temps t, si
au temps t, si
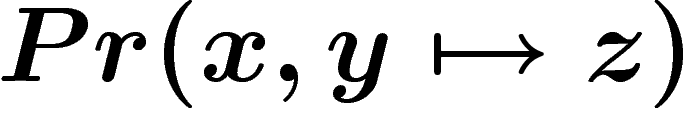 est la probabilité que, lors du croisement, les parents
x et y engendrent un enfant z, la loi
est la probabilité que, lors du croisement, les parents
x et y engendrent un enfant z, la loi 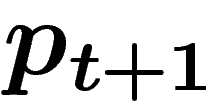 sur
sur 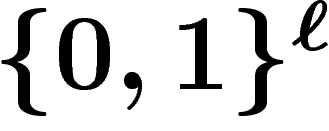 est donnée
par :
est donnée
par :
![\[
p_{t+1} (z) = \sum_{x,y \in \X} Pr(x,y\mapsto z)\, p_t(x)\,p_t(y)
\]](introag019.png)
On étudie donc un système quadratique et non linéaire.
Les systèmes dynamiques quadratiques peuvent avoir des comportements
complexes, mais la dynamique de l'opérateur de croisement génétique à
population infinie est bien connue (étude complète dans [RRS]).
En effet, ces auteurs montrent que la loi 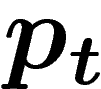 converge vers une loi
converge vers une loi
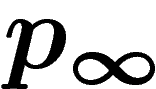 qui dépend de la population initiale
qui dépend de la population initiale 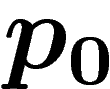 . La loi
. La loi 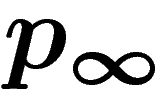 sur
sur 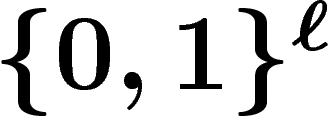 est définie comme suit : soit
est définie comme suit : soit 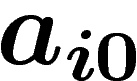 , pour
, pour 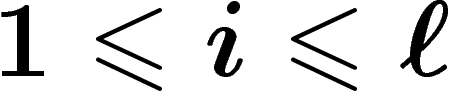 , la
probabilité dans
, la
probabilité dans 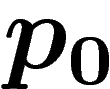 que le i-ième bit d'un individu soit un 0 ; soit
que le i-ième bit d'un individu soit un 0 ; soit
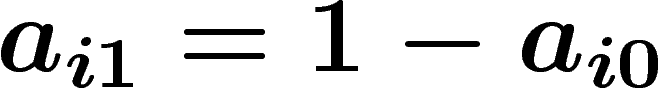 la probabilité que ce soit un 1. La loi
la probabilité que ce soit un 1. La loi 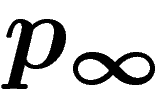 est
alors la loi sur
est
alors la loi sur 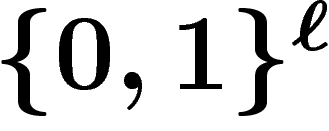 où chaque bit est choisi indépendamment des autres,
et vaut 0 avec probabilité
où chaque bit est choisi indépendamment des autres,
et vaut 0 avec probabilité 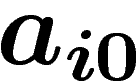 . Ainsi
. Ainsi
![\[p_\infty(x=x_1\ldots x_\ell)=\prod a_{ix_i}\]](introag032.png)
Par exemple, si 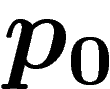 est composée pour moitié d'individus
est composée pour moitié d'individus  et
pour moitié de
et
pour moitié de  ,
, 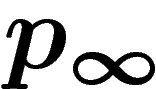 sera la probabilité uniforme sur
sera la probabilité uniforme sur
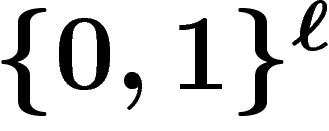 .
.
La vitesse de convergence est connue. Si on note
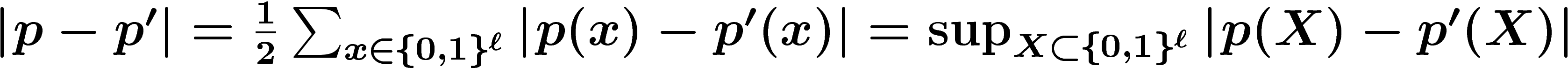 , on a :
, on a :
![\[
\abs{p_t-p_\infty}\leq \frac{\ell^2}{2^t}
\]](introag039.png)
ce qui indique une convergence assez rapide. Par ailleurs, on sait que
cette borne ne sera plus valable si on remplace 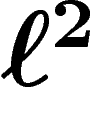 par
par 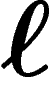 ; le terme
en
; le terme
en 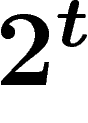 est correct.
est correct.
Étude du croisement en population finie.
Malheureusement,
l'étude en population finie n'est pas si simple. Cette fois-ci, on n'a
plus une suite déterministe de lois de probabilité 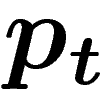 sur
sur 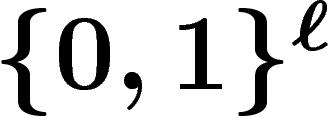 , mais
une suite de k-uplets aléatoires
, mais
une suite de k-uplets aléatoires 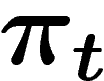 d'éléments de
d'éléments de 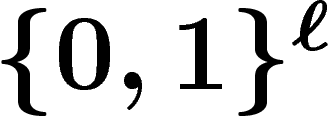 .
.
On voudrait dire que la population finie constitue une approximation de
la population infinie. Mais si l'on n'y prend pas garde, on risque des
corrélation inattendues : pour connaître un individu à la génération t,
il faut connaître ses deux parents, ses quatre grands-parents, etc.,
ses 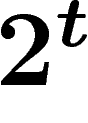 aïeux dans la population initiale. Si la taille de la
population est inférieure à
aïeux dans la population initiale. Si la taille de la
population est inférieure à 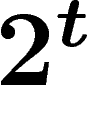 , des aïeux apparaîtront donc forcément
plusieurs fois, ce qui biaisera le processus (penser à
, des aïeux apparaîtront donc forcément
plusieurs fois, ce qui biaisera le processus (penser à  ).
).
Cette difficulté est générale dans un système quadratique. Elle a été
formalisée (cf. [ARV]): s'il était possible de simuler rapidement
tout système quadratique, on pourrait résoudre
en temps polynomial tout problème de classe PSpace (classe de problèmes
solubles avec une mémoire polynomiale ; contient NP).
Néanmoins, le cas de l'algorithme génétique est particulier et plus
simple. L'idée est que lors du croisement de deux individus, on délaisse
la moitié de l'information ; si un individu a 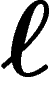 gènes, parmi ses
gènes, parmi ses 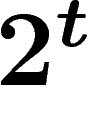 ancêtres, seuls
ancêtres, seuls 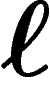 d'entre eux au plus ont transmis de l'information
génétique.
d'entre eux au plus ont transmis de l'information
génétique.
On va donc comparer le processus à population infinie 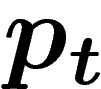 et le
processus à population finie
et le
processus à population finie 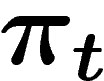 (où on initialise
(où on initialise 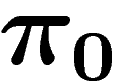 en tirant
k fois de suite un individu suivant la loi
en tirant
k fois de suite un individu suivant la loi 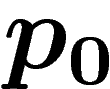 ).
).
Un dernier écueil est à éviter : on pourrait croire que le k-uplet
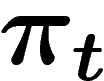 , vu comme une mesure sur
, vu comme une mesure sur 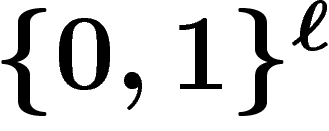 , constitue une approximation de la
mesure
, constitue une approximation de la
mesure 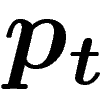 , mais il n'en est rien. Ceci est dû au phénomène bien connu de
coalescence : à chaque génération, une petite part de l'information
génétique est définitivement perdue (certains n'ont pas de descendants).
Aussi, au bout d'un certain temps, toute la population est-elle
constituée d'individus tous identiques. La répartition de
, mais il n'en est rien. Ceci est dû au phénomène bien connu de
coalescence : à chaque génération, une petite part de l'information
génétique est définitivement perdue (certains n'ont pas de descendants).
Aussi, au bout d'un certain temps, toute la population est-elle
constituée d'individus tous identiques. La répartition de 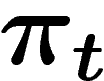 ne
donne donc certainement pas une bonne image de
ne
donne donc certainement pas une bonne image de 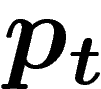 .
.
Cependant, l'individu qui compose cette population-clone est aléatoire
(c'est un mélange aléatoire de traits de la population de départ). On
peut donc espérer que sur plusieurs simulations de l'évolution à
population finie, la loi de l'individu-clone obtenu donnera une bonne
image de 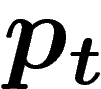 . Cet essai-ci est le bon. Soit
. Cet essai-ci est le bon. Soit 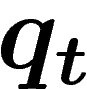 la loi d'un
individu tiré dans le k-uplet
la loi d'un
individu tiré dans le k-uplet 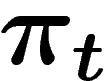 .
.
Y. Rabani, Y. Rabinovich et A. Sinclair démontrent alors :
![\[
\abs{q_t-p_t}\leq \frac{8\ell^2t}{k}
\]](introag065.png)
J'ai démontré en améliorant leur preuve que :
![\[
\abs{q_t-p_\infty}\leq \ell^2\left(\frac1k+\frac1{2^t}\right)
\]](introag066.png)
et par ailleurs que pour certaines populations initiales
![\[
\lim\abs{q_t-p_\infty} \geq \frac1k
\]](introag067.png)
[Addendum : je sais maintenant démontrer que pour certaines populations
initiales, 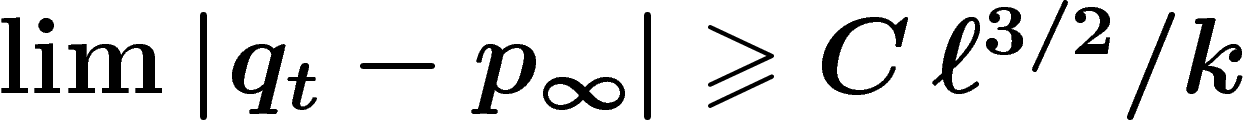 pour une certaine
constante C. Je n'ai pas pu inclure la démonstration en annexe.]
pour une certaine
constante C. Je n'ai pas pu inclure la démonstration en annexe.]
Application à la génération d'un élément aléatoire d'un groupe
fini.
Obtenir un élément aléatoire uniformément réparti dans un grand
groupe fini, étant donné une boîte noire qui multiplie deux éléments, et un
système générateur du groupe, constitue un problème classique.
Les méthodes classiques se font par marche aléatoire markovienne dans le
groupe : on a un élément qu'à chaque étape on multiplie par un élément
aléatoirement choisi dans un système générateur. Le temps de convergence
est généralement comme le carré du diamètre du graphe de Cayley du groupe
par rapport à ce système générateur (voir par exemple [DSC]).
Un autre algorithme (« product replacement algorithm » ou PRA) a été étudié
dans [CLMNO]. C'est une marche aléatoire sur l'ensemble des
k-uplets générateurs du groupe. À chaque étape, on choisit deux
éléments 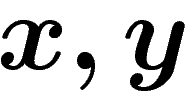 dans notre k-uplet générateur, et on les remplace par
le couple
dans notre k-uplet générateur, et on les remplace par
le couple 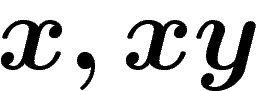 (ou
(ou 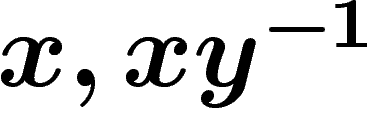 , ou
, ou 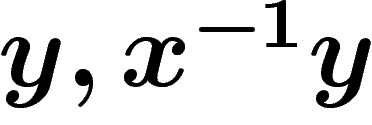 , ou...), ce qui donne
un nouveau k-uplet générateur.
, ou...), ce qui donne
un nouveau k-uplet générateur.
Évidemment, ceci ressemble à un algorithme génétique où l'opérateur de
croisement serait simplement le produit de deux éléments. L'algorithme à
population infinie reviendrait à prendre une mesure de probabilité sur le
groupe et à la convoler avec elle-même, ce qui converge extrêmement vite.
L'étude théorique du PRA n'était pas très avancée (le graphe des
k-uplets générateurs n'est même pas forcément connexe pour les
opérations permises). Récemment, I. Pak a montré (cf. [Pak]) que le
PRA converge, sur l'ensemble des k-uplets générateurs, pour k de
l'ordre de 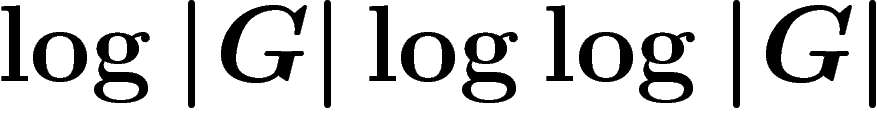 , en un nombre d'itérations de
l'ordre de
, en un nombre d'itérations de
l'ordre de 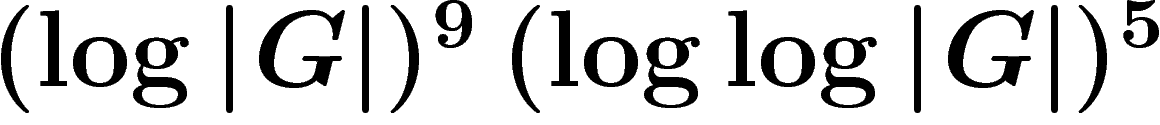 .
.
Cependant, cette convergence a lieu dans l'ensemble des k-uplets
générateurs. Il est bien différent de demander qu'un des éléments du
k-uplet obtenu soit uniformément réparti dans le groupe. D'une part, on
demande une convergence sur les k-uplets ce qui est de plus en plus
difficile quand k augmente, alors qu'intuitivement on attend qu'un plus
grand k approxime mieux le processus à population infinie, et qu'il se
peut que la convergence soit plus rapide quand on ne regarde qu'une
composante. D'autre part, L. Babai et I. Pak ont démontré
(voir [BP]) qu'une composante d'un k-uplet générateur aléatoire
uniformément choisi parmi ces k-uplets générateurs n'est pas
uniformément répartie dans le groupe (par exemple l'élément neutre
apparaît moins souvent dans les systèmes générateurs) ; ceci limite
l'intérêt de l'algorithme pour le problème initial.
On peut donc envisager un autre algorithme : maintenir une population
quelconque (pas forcément un ensemble générateur) et, à chaque étape,
remplacer cette population par des produits d'éléments de cette
population (on doit ajouter une probabilité de ne rien changer, pour
éviter des phénomènes de périodicité). On obtient ainsi un « algorithme
génétique sur les groupes ».
Quand la taille de la population est assez
grande, je peux montrer que cet algorithme engendre bien un élément
aléatoire uniformément tiré dans le groupe, mais pour l'instant je ne
sais pas montrer que cet algorithme est plus efficace, en terme de nombre
d'étapes, que la méthode markovienne classique par convolutions.
Références
[ARV] S. Arora, Y. Rabani, U. Vazirani, Simulating
quadratic dynamical systems is PSpace-complete, Proceedings of the
Twenty-Sixth Annual ACM Symposium on Theory of Computing (1994),
p. 459--467.
[BP] L. Babai, I. Pak, Strong bias of group generators:
an obstacle to the "product replacement algorithm", Proc. SODA'00,
p. 627--635.
[CLMNO] F. Celler, C. R. Leedham-Green, S. Murray,
A. Niemeyer, E. A. O'Brien, Generating random elements of a finite
group, Comm. Alg. 23 (1995), p. 4931--4948.
[DSC] P. Diaconis, L. Saloff-Coste,
An application of Harnack inequalities to random walk on
nilpotent quotients, J. Fourier Anal. Appl., Kahane special issue
(1995), p. 198--207.
[Pak] I. Pak, The product replacement algorithm is
polynomial, en cours de publication.
[RRS] Y. Rabani, Y. Rabinovich et A. Sinclair, A computational view of population
genetics, Random Structures and Algorithms 12 (1998), 4,
p. 313--334.
Back to: Main Page > Mathématiques
To leave a comment: contact (domain) yann-ollivier.org
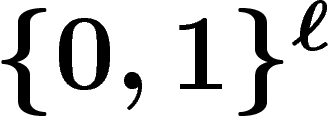 (on code les solutions du
problème par des suites de 0 et de 1). La mutation consiste alors à
changer probabilistement un petit nombre de bits (généralement, on change
chaque bit aléatoirement, indépendamment des autres, avec une probabilité
de l'ordre de
(on code les solutions du
problème par des suites de 0 et de 1). La mutation consiste alors à
changer probabilistement un petit nombre de bits (généralement, on change
chaque bit aléatoirement, indépendamment des autres, avec une probabilité
de l'ordre de 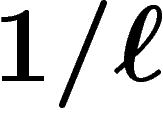 ).
).
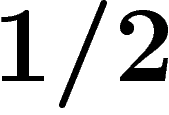 ,
indépendamment, si on prendra celui de l'un ou l'autre parent. Par la
suite, pour la simplicité de l'exposé, on se tiendra à cette dernière
possibilité.
,
indépendamment, si on prendra celui de l'un ou l'autre parent. Par la
suite, pour la simplicité de l'exposé, on se tiendra à cette dernière
possibilité.
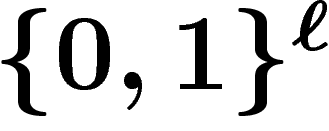 ; choisir une taille de
population k ; définir la fonction
; choisir une taille de
population k ; définir la fonction 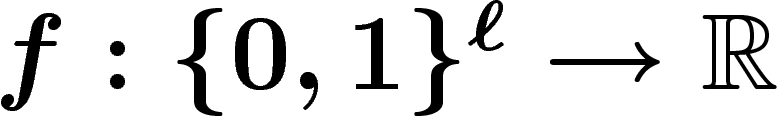 à optimiser ;
à optimiser ;
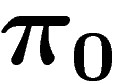 d'éléments de
d'éléments de 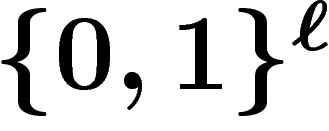 quelconques ;
quelconques ;
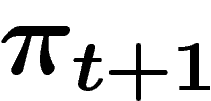 à partir
de
à partir
de 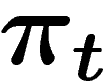 en répétant k fois de suite indépendamment les opérations
suivantes :
en répétant k fois de suite indépendamment les opérations
suivantes :
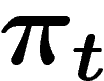 avec une
probabilité proportionnelle à la valeur de f sur ces individus,
avec une
probabilité proportionnelle à la valeur de f sur ces individus,
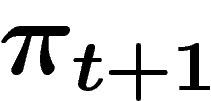 ;
;
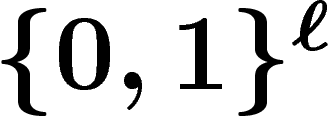 est incongru).
est incongru).
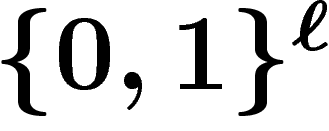 , l'évolution de ces lois étant déterministe. Si
, l'évolution de ces lois étant déterministe. Si
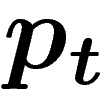 désigne la loi de probabilité obtenue sur
désigne la loi de probabilité obtenue sur 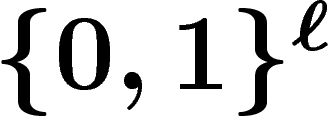 au temps t, si
au temps t, si
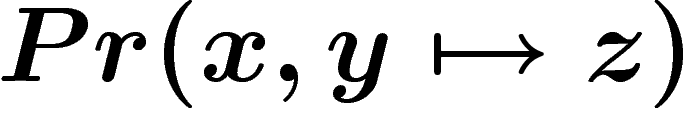 est la probabilité que, lors du croisement, les parents
x et y engendrent un enfant z, la loi
est la probabilité que, lors du croisement, les parents
x et y engendrent un enfant z, la loi 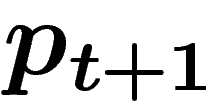 sur
sur 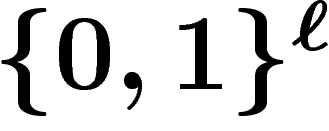 est donnée
par :
est donnée
par :
![\[
p_{t+1} (z) = \sum_{x,y \in \X} Pr(x,y\mapsto z)\, p_t(x)\,p_t(y)
\]](introag019.png)
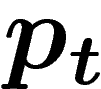 converge vers une loi
converge vers une loi
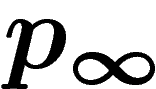 qui dépend de la population initiale
qui dépend de la population initiale 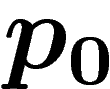 . La loi
. La loi 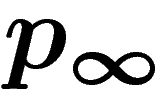 sur
sur 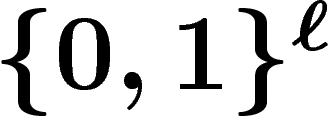 est définie comme suit : soit
est définie comme suit : soit 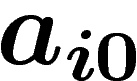 , pour
, pour 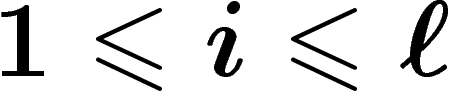 , la
probabilité dans
, la
probabilité dans 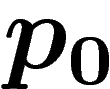 que le i-ième bit d'un individu soit un 0 ; soit
que le i-ième bit d'un individu soit un 0 ; soit
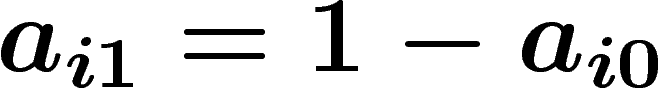 la probabilité que ce soit un 1. La loi
la probabilité que ce soit un 1. La loi 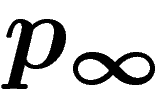 est
alors la loi sur
est
alors la loi sur 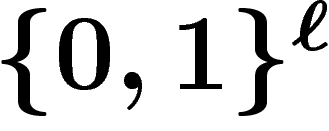 où chaque bit est choisi indépendamment des autres,
et vaut 0 avec probabilité
où chaque bit est choisi indépendamment des autres,
et vaut 0 avec probabilité 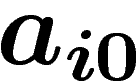 . Ainsi
. Ainsi
![\[p_\infty(x=x_1\ldots x_\ell)=\prod a_{ix_i}\]](introag032.png)
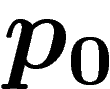 est composée pour moitié d'individus
est composée pour moitié d'individus  et
pour moitié de
et
pour moitié de  ,
, 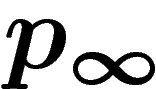 sera la probabilité uniforme sur
sera la probabilité uniforme sur
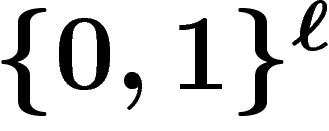 .
.
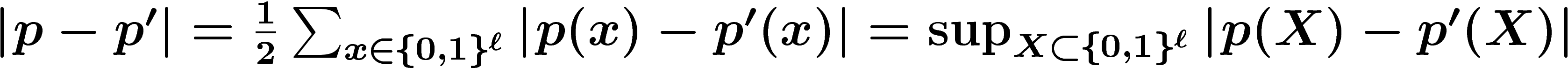 , on a :
, on a :
![\[
\abs{p_t-p_\infty}\leq \frac{\ell^2}{2^t}
\]](introag039.png)
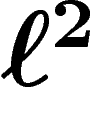 par
par 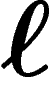 ; le terme
en
; le terme
en 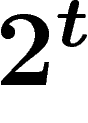 est correct.
est correct.
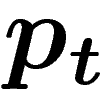 sur
sur 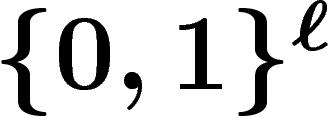 , mais
une suite de k-uplets aléatoires
, mais
une suite de k-uplets aléatoires 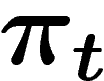 d'éléments de
d'éléments de 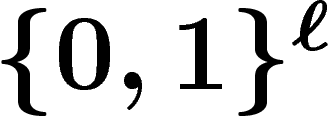 .
.
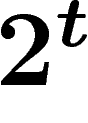 aïeux dans la population initiale. Si la taille de la
population est inférieure à
aïeux dans la population initiale. Si la taille de la
population est inférieure à 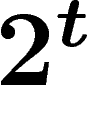 , des aïeux apparaîtront donc forcément
plusieurs fois, ce qui biaisera le processus (penser à
, des aïeux apparaîtront donc forcément
plusieurs fois, ce qui biaisera le processus (penser à 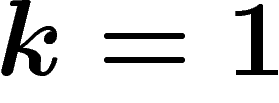 ).
).
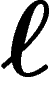 gènes, parmi ses
gènes, parmi ses 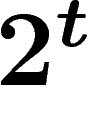 ancêtres, seuls
ancêtres, seuls 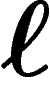 d'entre eux au plus ont transmis de l'information
génétique.
d'entre eux au plus ont transmis de l'information
génétique.
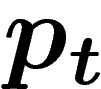 et le
processus à population finie
et le
processus à population finie 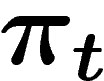 (où on initialise
(où on initialise 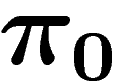 en tirant
k fois de suite un individu suivant la loi
en tirant
k fois de suite un individu suivant la loi 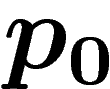 ).
).
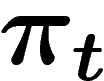 , vu comme une mesure sur
, vu comme une mesure sur 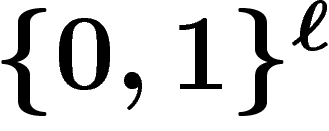 , constitue une approximation de la
mesure
, constitue une approximation de la
mesure 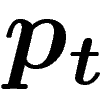 , mais il n'en est rien. Ceci est dû au phénomène bien connu de
coalescence : à chaque génération, une petite part de l'information
génétique est définitivement perdue (certains n'ont pas de descendants).
Aussi, au bout d'un certain temps, toute la population est-elle
constituée d'individus tous identiques. La répartition de
, mais il n'en est rien. Ceci est dû au phénomène bien connu de
coalescence : à chaque génération, une petite part de l'information
génétique est définitivement perdue (certains n'ont pas de descendants).
Aussi, au bout d'un certain temps, toute la population est-elle
constituée d'individus tous identiques. La répartition de 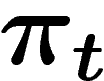 ne
donne donc certainement pas une bonne image de
ne
donne donc certainement pas une bonne image de 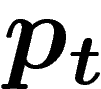 .
.
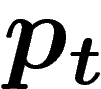 . Cet essai-ci est le bon. Soit
. Cet essai-ci est le bon. Soit 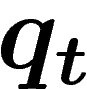 la loi d'un
individu tiré dans le k-uplet
la loi d'un
individu tiré dans le k-uplet 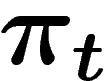 .
.
![\[
\abs{q_t-p_t}\leq \frac{8\ell^2t}{k}
\]](introag065.png)
![\[
\abs{q_t-p_\infty}\leq \ell^2\left(\frac1k+\frac1{2^t}\right)
\]](introag066.png)
![\[
\lim\abs{q_t-p_\infty} \geq \frac1k
\]](introag067.png)
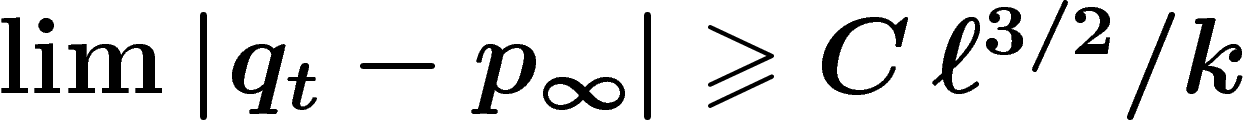 pour une certaine
constante C. Je n'ai pas pu inclure la démonstration en annexe.]
pour une certaine
constante C. Je n'ai pas pu inclure la démonstration en annexe.]
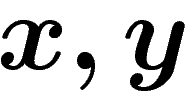 dans notre k-uplet générateur, et on les remplace par
le couple
dans notre k-uplet générateur, et on les remplace par
le couple 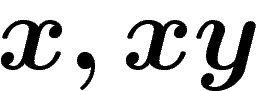 (ou
(ou 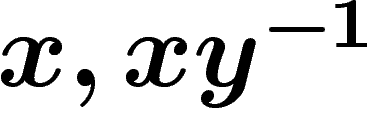 , ou
, ou 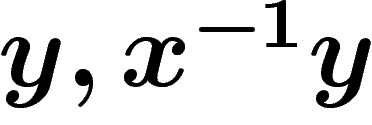 , ou...), ce qui donne
un nouveau k-uplet générateur.
, ou...), ce qui donne
un nouveau k-uplet générateur.
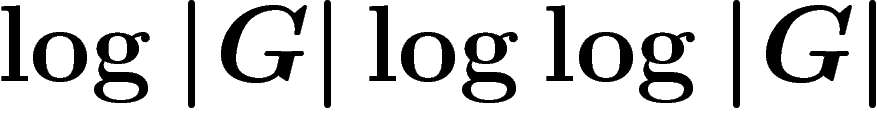 , en un nombre d'itérations de
l'ordre de
, en un nombre d'itérations de
l'ordre de 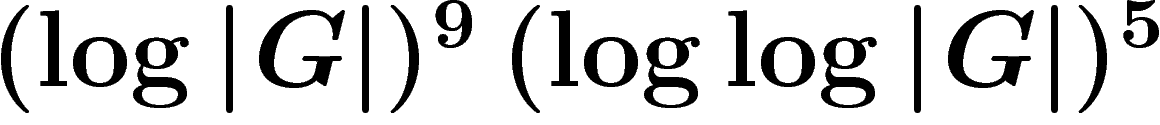 .
.