 un système générateur
symétrique de G.
On définit une géométrie sur G :
un système générateur
symétrique de G.
On définit une géométrie sur G :
- la longueur d'un élément
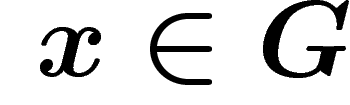 est la plus petite
longueur d'une suite
est la plus petite
longueur d'une suite  de générateurs telle que
de générateurs telle que
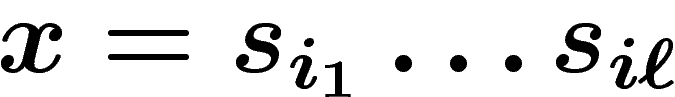 ;
;
- la distance entre deux éléments
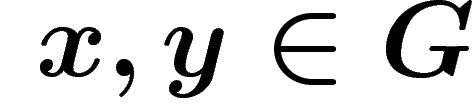 est la longueur
de
est la longueur
de 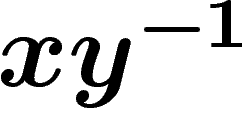 .
.
Yann Ollivier, avril 2001
Aussi au format pdf ou ps gzippé
Nous donnons ici une introduction à différents thèmes liés à la géométrie des groupes discrets. On s'intéressera en particulier à des propriétés asymptotiques des groupes discrets infinis. On commence par donner un aperçu des propriétés usuellement étudiées (par exemple la propriété de Kazhdan, l'hyperbolicité, la moyennabilité), avec des exemples, et l'on énonce quelques-uns des « grands » théorèmes de ce domaine, sans démonstration.
Puis nous montrons comment la propriété de Kazhdan mentionnée plus haut peut aider à résoudre un problème classique de géométrie algorithmique des groupes, celui de trouver une méthode pour obtenir un élément aléatoire dans un groupe fini donné par des générateurs et une boîte noire effectuant la multiplication. L'idée d'un algorithme couramment utilisé sans démonstration, le PRA, est d'effectuer une marche aléatoire sur le graphe des k-uplets générateurs du groupe (voir section PRA pour une définition précise). En définissant une action d'un certain groupe de Kazhdan sur ce graphe, on peut obtenir une évaluation du temps de convergence, qui fait l'objet du théorème final que nous démontrerons.
On donne ci-dessous une définition des groupes discrets. Des extensions sont possibles (en particulier, certaines des notions mentionnées plus loin sont définies dans le cadre des groupes localement compacts), mais nous nous en tiendrons à ce cadre (relativement) simple. Cette présentation est inspirée de l'excellent [GH].
De plus, pour dépasser un peu cette définition, on voudrait faire de la géométrie sur ces groupes, et on voudrait donc introduire une notion de distance. C'est possible en choisissant un système de générateurs donné.
On dit qu'un système de générateurs est symétrique s'il contient les inverses de ses éléments.
 un système générateur
symétrique de G.
On définit une géométrie sur G :
un système générateur
symétrique de G.
On définit une géométrie sur G :
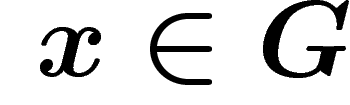 est la plus petite
longueur d'une suite
est la plus petite
longueur d'une suite  de générateurs telle que
de générateurs telle que
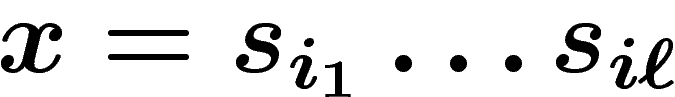 ;
;
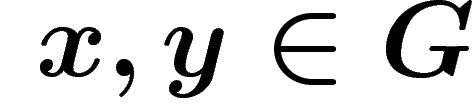 est la longueur
de
est la longueur
de 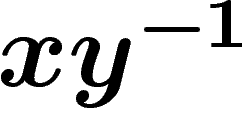 .
.
Il est immédiat de vérifier que cette distance en est bien une : si on
peut passer de x à y en multipliant par 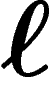 générateurs et de y
à z par
générateurs et de y
à z par 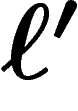 générateurs, on peut passer de x à z par
générateurs, on peut passer de x à z par
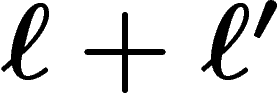 générateurs.
générateurs.
Par construction, elle est invariante par multiplication à gauche.
Cette distance peut s'interpréter comme distance dans un graphe :
 un système générateur
symétrique de G.
Le graphe de Cayley de G par rapport à ce système générateur est
le graphe dont les sommets sont les éléments de G, avec une arête entre
x et y si et seulement s'il existe
un système générateur
symétrique de G.
Le graphe de Cayley de G par rapport à ce système générateur est
le graphe dont les sommets sont les éléments de G, avec une arête entre
x et y si et seulement s'il existe 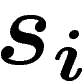 tel que
tel que 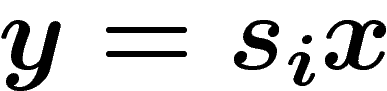 .
.
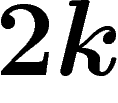 (ce qui peut servir comme
définition géométrique du groupe libre : l'absence de relation est
l'absence de cycles dans le graphe).
(ce qui peut servir comme
définition géométrique du groupe libre : l'absence de relation est
l'absence de cycles dans le graphe).
Un groupe agit naturellement par multiplication à gauche sur son graphe de Cayley.
Ces notions dépendent bien entendu du système générateur choisi. Pour étudier cette dépendance, on introduit la notion suivante :
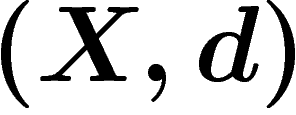 et
et 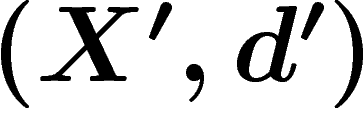 deux espaces métriques. On dit qu'ils sont
quasi-isométriques s'il existe des applications
deux espaces métriques. On dit qu'ils sont
quasi-isométriques s'il existe des applications 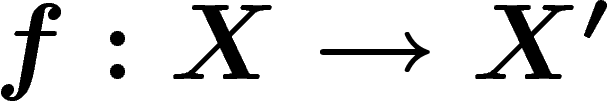 et
et 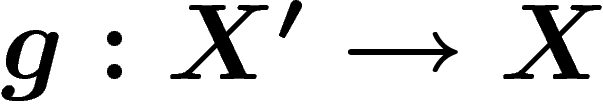 , ainsi que des constantes
, ainsi que des constantes 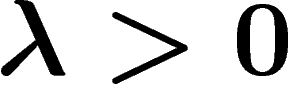 et
et
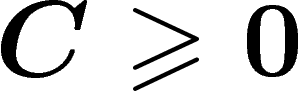 telles que pour tous
telles que pour tous 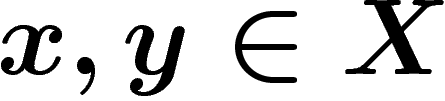 ,
, 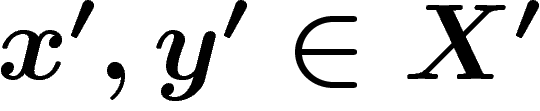 :
:
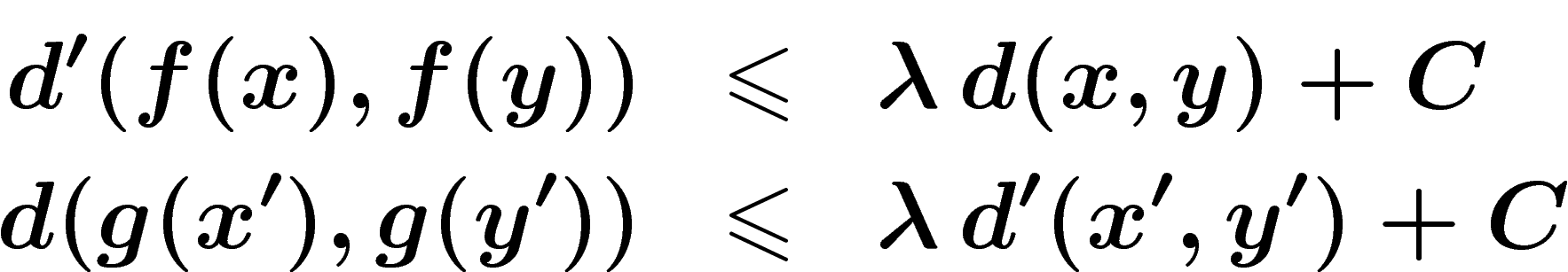
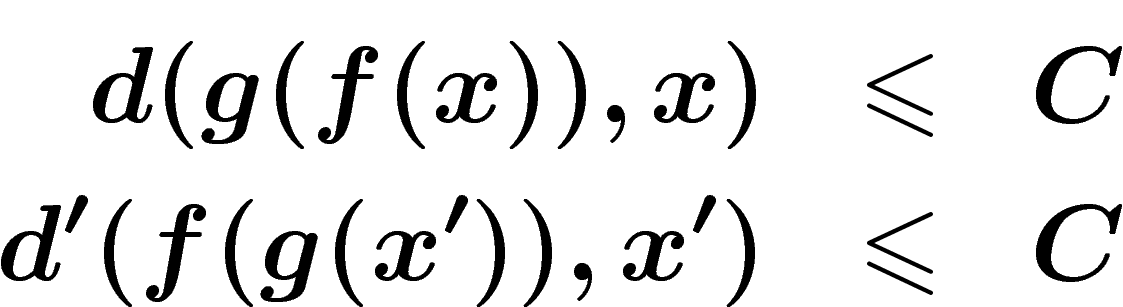
Ainsi, excepté à petite distance, les fonctions f et g sont presque lipschitziennes et presque inverses.
La quasi-isométrie est une relation d'équivalence sur les espaces métriques.
Nous considérerons donc les groupes discrets comme des espaces métriques à quasi-isométrie près. En particulier, nous définirons souvent des propriétés d'un groupe en regardant son graphe de Cayley pour un certain système générateur, et en vérifiant que la propriété est invariante par quasi-isométrie.
 et
et 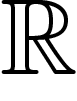 sont quasi-isométriques. Un
sous-groupe d'indice fini dans un groupe discret lui est
quasi-isométrique.
sont quasi-isométriques. Un
sous-groupe d'indice fini dans un groupe discret lui est
quasi-isométrique.
Un théorème de M. Gromov affirme qu'un théorème valable pour tous les groupes est soit trivial soit faux. Par conséquent, pour démontrer des théorèmes vrais et intéressants, on doit se restreindre à des sous-classes de groupes possédant certaines propriétés. Nous en présentons ici trois : la moyennabilité, l'hyperbolicité et la propriété (T) de Kazhdan. C'est cette dernière qui nous servira de manière cruciale par la suite.
Ces notions reflètent véritablement des propriétés des groupes infinis. En effet, tous les groupes finis les vérifient.
Groupes moyennables. Les groupes moyennables
sont ceux dans lesquels les effets de bord sont négligeables lorsqu'on
considère des sous-parties assez grandes (cf. les problèmes de conditions
aux limites en physique). Ainsi 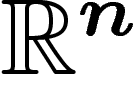 ou
ou 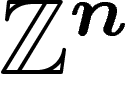 sont moyennables, car le
rapport de la mesure du bord d'une boule à la mesure de la boule tend
vers
sont moyennables, car le
rapport de la mesure du bord d'une boule à la mesure de la boule tend
vers  quand la boule devient grande.
quand la boule devient grande.
Dans un graphe, le bord d'une partie A, noté 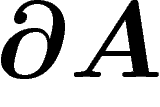 , est
défini comme l'ensemble des points du complémentaire de A joints par
une arête à un point de A.
, est
défini comme l'ensemble des points du complémentaire de A joints par
une arête à un point de A.
![\[
\inf \left\{\frac{\abs{\partial A}}{\abs{A}}, A\subset G\text{ fini non
vide}\right\}=0
\]](introgroupes030.png)
On vérifie aisément que cette notion est invariante par quasi-isométrie, donc bien définie pour un groupe à partir d'un graphe de Cayley.
On peut montrer que :
Groupes hyperboliques. La notion de groupe hyperbolique est une invention de M. Gromov (cf. [Gr]), s'inspirant des variétés hyperboliques (à courbure négative).
Dans un graphe, on appelle triangle la donnée de trois sommets, et de trois chemins de longueur minimale (ces chemins ne sont pas forcément uniques) reliant ces sommets deux à deux, qu'on appelle côtés du triangle.
Dans un plan hyperbolique habituel, les côtés des triangles ont la propriété d'êtres courbés vers l'intérieur, au sens où la distance d'un point d'un côté à la réunion des deux autres côtés est toujours inférieure à ce qu'elle serait dans un triangle euclidien... en fait elle est même bornée. Ceci sert de base à une définition des groupes hyperboliques.
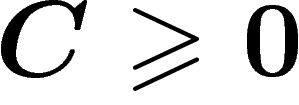 telle que pour tout triangle,
la distance d'un point d'un côté du triangle à la réunion des deux autres
côtés est inférieure à C.
telle que pour tout triangle,
la distance d'un point d'un côté du triangle à la réunion des deux autres
côtés est inférieure à C.
Il est vrai, mais pas du tout trivial, que cette propriété ne dépend pas du graphe de Cayley choisi (elle est invariante par quasi-isométrie).
Voici une autre justification du nom :
Il existe de nombreuses définitions équivalentes de l'hyperbolicité d'un groupe, de nature géométrique ou combinatoire (cf. [GH]). Par exemple, l'une d'elles est obtenue en formalisant précisément l'intuition que vu de loin, le graphe de Cayley d'un groupe hyperbolique ressemble à un arbre.
Propriété (T) de Kazhdan. Une notion supplémentaire, d'apparence abstraite, s'est révélée extrêmement féconde dans des domaines très variés de l'étude des groupes, de la théorie des graphes, de la théorie de la mesure et même en informatique : c'est la propriété (T) de Kazhdan. Elle est très bien présentée dans [HV]. Elle est plus généralement définie pour des groupes localement compacts, et ci-dessous nous dirons souvent « compact » là où « fini » aurait le même sens dans le cadre des groupes discrets.
d'un groupe discret G est une action
de G par des isométries linéaires sur un espace de Hilbert 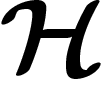 , ou
encore un morphisme de G vers les endomorphismes unitaires de
, ou
encore un morphisme de G vers les endomorphismes unitaires de 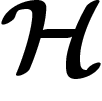 .
.
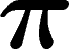 de G sur un Hilbert
de G sur un Hilbert 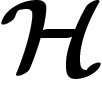 a
des vecteurs invariants s'il existe
a
des vecteurs invariants s'il existe 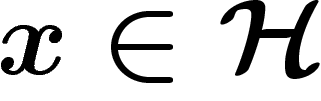 non nul tel que pour
tout
non nul tel que pour
tout 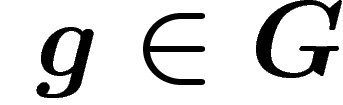 ,
, 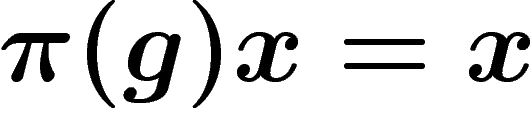 .
.
On dit que  a des vecteurs presque invariants si pour tout
a des vecteurs presque invariants si pour tout 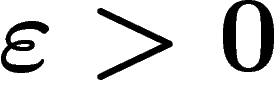 ,
pour tout compact
,
pour tout compact  , on peut trouver un
, on peut trouver un 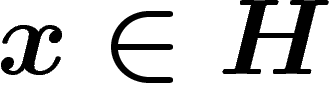 non nul tel
que pour tout
non nul tel
que pour tout 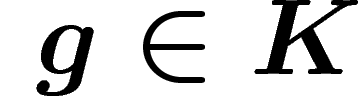 ,
, 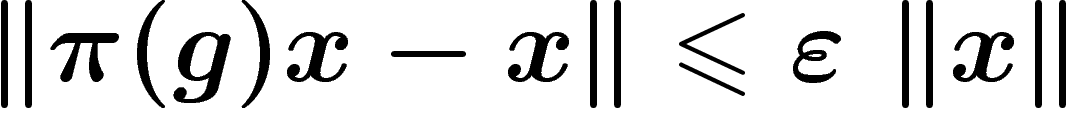 .
.
Cette condition porte sur toutes les représentations, et est donc extrêmement forte. En fait, selon la proposition ci-dessous, il suffit de la tester sur un compact générateur de G et sur les représentations irréductibles, puisque d'autres représentations et d'autres éléments du groupe peuvent être obtenus par construction sur ceux-là.
On rappelle qu'une représentation d'un groupe sur un espace 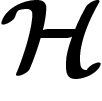 est
irréductible si l'on ne peut pas trouver de décomposition
est
irréductible si l'on ne peut pas trouver de décomposition
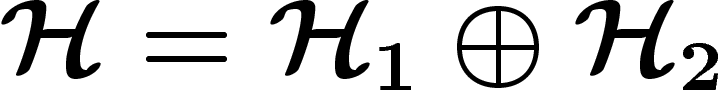 telle que
telle que 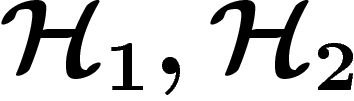 sont stables par l'action de la
représentation. Toute représentation peut se décomposer en une somme de
représentations irréductibles.
sont stables par l'action de la
représentation. Toute représentation peut se décomposer en une somme de
représentations irréductibles.
 tel que toute représentation unitaire irréductible de G
possédant des vecteurs unitaires
tel que toute représentation unitaire irréductible de G
possédant des vecteurs unitaires 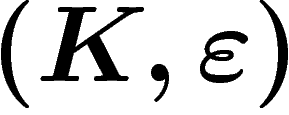 -invariants, possède des
vecteurs invariants. Alors G est de Kazhdan.
-invariants, possède des
vecteurs invariants. Alors G est de Kazhdan.
Le couple 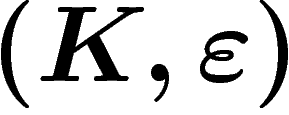 est appelé une constante de Kazhdan de G.
est appelé une constante de Kazhdan de G.
On peut montrer :
Mais aussi :
 n'est pas de Kazhdan.
n'est pas de Kazhdan.
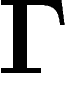 , qui définit une représentation de G sur
, qui définit une représentation de G sur 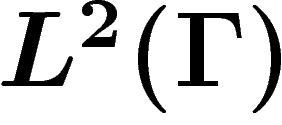 par translation (représentation régulière gauche). Si G est
moyennable, en prenant un ensemble A grand et de petit bord, une
fonction constante sur A est presque invariante, car si on la translate
par des éléments de G, la différence est concentrée vers le bord de
A. Si le groupe était de Kazhdan, il existerait donc une fonction
invariante ; comme l'action de G sur son graphe de Cayley est
transitive, cette fonction serait constante. Or dès que G est infini,
il n'y a évidemment pas de fonction constante non nulle
par translation (représentation régulière gauche). Si G est
moyennable, en prenant un ensemble A grand et de petit bord, une
fonction constante sur A est presque invariante, car si on la translate
par des éléments de G, la différence est concentrée vers le bord de
A. Si le groupe était de Kazhdan, il existerait donc une fonction
invariante ; comme l'action de G sur son graphe de Cayley est
transitive, cette fonction serait constante. Or dès que G est infini,
il n'y a évidemment pas de fonction constante non nulle 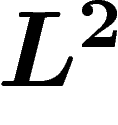 -intégrable
sur
-intégrable
sur 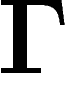 .
CQFD.
.
CQFD.En particulier, ces propriétés mises bout à bout montrent qu'un groupe de Kazhdan est très non commutatif, au sens ou son abélianisé est compact (en effet, il est de Kazhdan comme image d'un groupe de Kazhdan, et il est abélien donc moyennable, donc compact). Ceci permet de dire, par exemple, qu'un groupe libre n'est pas de Kazhdan.
Il existe d'autres définitions de la propriété de Kazhdan. L'une d'elles demande que toute action affine isométrique du groupe sur un Hilbert ait un point fixe. Une autre est en rapport avec la cohomologie du groupe...
Jusqu'ici, nous n'avons guère vu d'exemples intéressants. On va
s'intéresser à 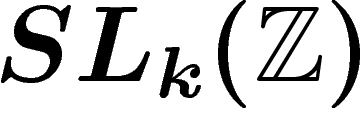 qui nous resservira par la suite. On sait que
ce groupe est de Kazhdan, et on a même une évaluation de la constante de
Kazhdan par rapport aux matrices élémentaires. Une matrice
élémentaire dans
qui nous resservira par la suite. On sait que
ce groupe est de Kazhdan, et on a même une évaluation de la constante de
Kazhdan par rapport aux matrices élémentaires. Une matrice
élémentaire dans 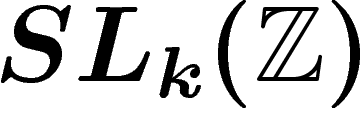 est une matrice qui ne contient que des
est une matrice qui ne contient que des  sur la diagonale, qui contient un unique
sur la diagonale, qui contient un unique 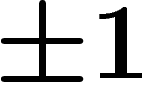 quelque part en-dehors
de la diagonale, et des
quelque part en-dehors
de la diagonale, et des  ailleurs. Ces matrices engendrent
ailleurs. Ces matrices engendrent 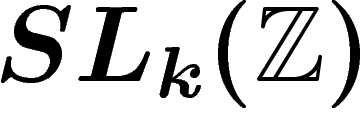 .
Un raisonnement élaboré montre alors, avec des outils relativement
élémentaires, que (cf [Sh]) :
.
Un raisonnement élaboré montre alors, avec des outils relativement
élémentaires, que (cf [Sh]) :
Nous utiliserons ce théorème plus loin, dans notre étude de la convergence des marches aléatoires dans les groupes.
Mentionnons enfin le
Prouver qu'un groupe est hyperbolique ou de Kazhdan est souvent difficile. Cependant, on peut montrer qu'en un certain sens, presque tous les groupes sont hyperboliques, et, qu'au-dessus d'une certaine densité de relations, presque tous les groupes sont de Kazhdan. Ce sont les très élégants théorèmes que nous énonçons ici.
L'idée est de partir du groupe libre engendré par  , et de
construire des groupes en quotientant par des relations (une relation est
simplement un mot en les
, et de
construire des groupes en quotientant par des relations (une relation est
simplement un mot en les 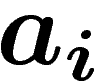 et
et 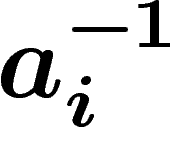 ). Tout groupe à k
générateurs peut être obtenu de la sorte. Si on met beaucoup de
relations, on a des chances que le quotient soit simplement le groupe
trivial. On va choisir la quantité de relations que l'on met à partir
d'une densité, que nous définissons maintenant.
). Tout groupe à k
générateurs peut être obtenu de la sorte. Si on met beaucoup de
relations, on a des chances que le quotient soit simplement le groupe
trivial. On va choisir la quantité de relations que l'on met à partir
d'une densité, que nous définissons maintenant.
On fixe le nombre k de générateurs. On considère les groupes présentés
par ces k générateurs, et des relations de longueur 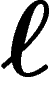 entre ces
générateurs. Si l'on simplifie les relations contenant les sous-mots
triviaux
entre ces
générateurs. Si l'on simplifie les relations contenant les sous-mots
triviaux 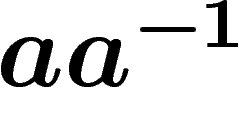 , le nombre de mots de longueur
, le nombre de mots de longueur 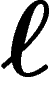 sur k
générateurs est
sur k
générateurs est 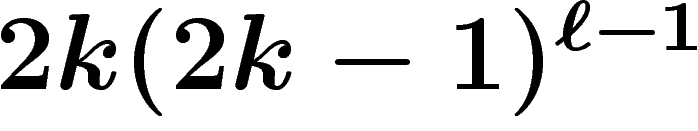 . Soit un groupe G présenté par r
relations de longueur
. Soit un groupe G présenté par r
relations de longueur 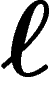 . On dit que cette présentation est de
densité d si
. On dit que cette présentation est de
densité d si  pour une
certaine constante
pour une
certaine constante 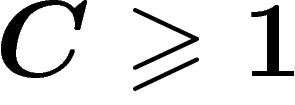 .
.
On définit un groupe aléatoire 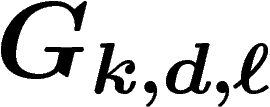 à k générateurs, avec
densité d et relations de longueur
à k générateurs, avec
densité d et relations de longueur 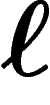 , comme le groupe obtenu en
prenant une présentation uniformément au hasard parmi toutes les
présentations sur k générateurs, de densité d et de relations de
longueur
, comme le groupe obtenu en
prenant une présentation uniformément au hasard parmi toutes les
présentations sur k générateurs, de densité d et de relations de
longueur 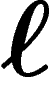 .
.
Alors, si on a beaucoup de relations, on obtient presque sûrement le groupe trivial ; si on a peu de relations, on obtient presque sûrement un groupe hyperbolique.
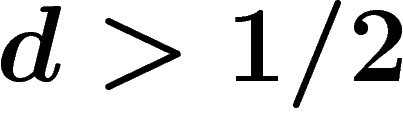 , quand
, quand 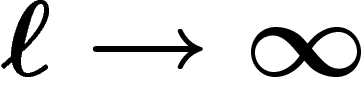 , la probabilité que
, la probabilité que
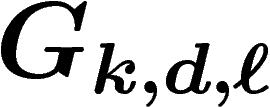 soit le groupe trivial
soit le groupe trivial 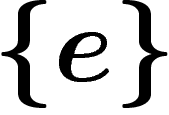 tend vers 1.
tend vers 1.
Si 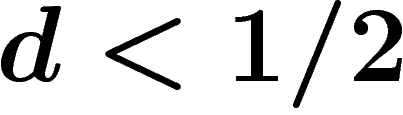 , quand
, quand 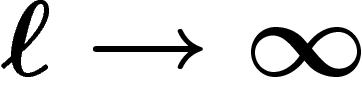 , la probabilité que
, la probabilité que
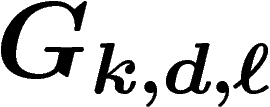 soit infini et hyperbolique tend vers 1.
soit infini et hyperbolique tend vers 1.
Ce qui se produit à la densité critique 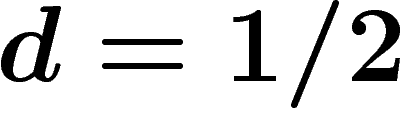 reste un mystère.
reste un mystère.
Par ailleurs :
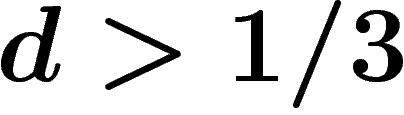 , quand
, quand 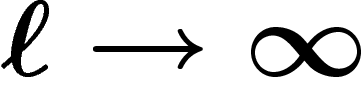 , la probabilité que
, la probabilité que
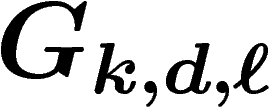 soit de Kazhdan tend vers 1.
soit de Kazhdan tend vers 1.
En particulier, entre 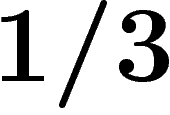 et
et 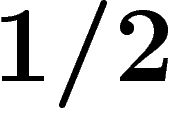 , on a des groupes non triviaux
hyperboliques de Kazhdan.
, on a des groupes non triviaux
hyperboliques de Kazhdan.
On donne ici quelques rappels sur les marches aléatoires dans les graphes, et, en particulier, dans des graphes de Cayley. Tous les graphes que nous considérerons seront orientés, avec éventuellement des boucles et des arêtes multiples. On supposera aussi que de chaque point il part au moins une arête.
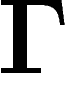 un graphe. On appelle marche aléatoire sur
un graphe. On appelle marche aléatoire sur 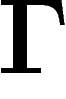 le processus markovien qui, partant d'un point quelconque, se déplace
vers un point voisin en choisissant une arête au hasard uniformément
parmi toutes les arêtes partant de ce point.
le processus markovien qui, partant d'un point quelconque, se déplace
vers un point voisin en choisissant une arête au hasard uniformément
parmi toutes les arêtes partant de ce point.
À chaque étape, on note 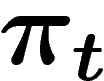 la mesure sur
la mesure sur 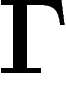 qui est la loi du
point atteint au temps t par la marche aléatoire.
qui est la loi du
point atteint au temps t par la marche aléatoire.
La marche aléatoire peut être vue comme un opérateur h sur les
mesures sur 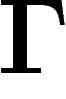 ou, plus généralement, sur les fonctions sur
ou, plus généralement, sur les fonctions sur
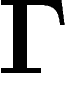 dans
dans 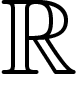 ou
ou  , défini par :
, défini par :
![\[
(h.f)(x)=\sum_{y\sim x} \frac{1}{\deg y}f(y)
\]](introgroupes099.png)
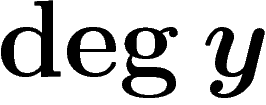 est le nombre d'arêtes partant de y et où
est le nombre d'arêtes partant de y et où  signifie qu'il y a une arête allant de y à x. On a alors
signifie qu'il y a une arête allant de y à x. On a alors
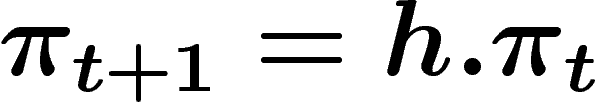 .
.
L'opérateur 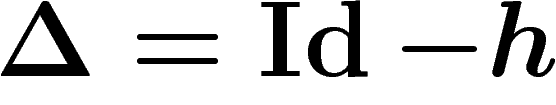 est appelé laplacien sur le graphe.
est appelé laplacien sur le graphe.
 .
.
Désormais, on ne considérera plus que des graphes réguliers symétriques. C'est en particulier le cas du graphe de Cayley d'un groupe.
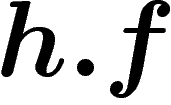 en un
point est la moyenne de la valeur de f sur ses voisins. Regarder un
point où f est de module maximal (il en existe car le graphe est fini),
en déduire que f a la même valeur sur tous les voisins et utiliser la
connexité (connexité au sens des graphes orientés).
CQFD.
en un
point est la moyenne de la valeur de f sur ses voisins. Regarder un
point où f est de module maximal (il en existe car le graphe est fini),
en déduire que f a la même valeur sur tous les voisins et utiliser la
connexité (connexité au sens des graphes orientés).
CQFD.
Si 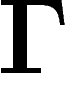 est le graphe de Cayley d'un groupe G pour un système de
générateurs S, alors h est l'opérateur de convolution (à gauche) avec
la fonction qui vaut
est le graphe de Cayley d'un groupe G pour un système de
générateurs S, alors h est l'opérateur de convolution (à gauche) avec
la fonction qui vaut 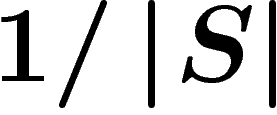 en chaque générateur de S, et
en chaque générateur de S, et  ailleurs.
ailleurs.
Notons que si le graphe est régulier de degré d et symétrique,
alors l'opérateur h sur 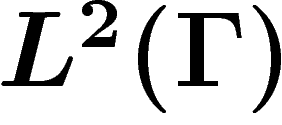 est autoadjoint. En effet :
est autoadjoint. En effet :
![\[
\langle h.f ,g\rangle =
\sum (h.f)(x)\,g(x)
=
\sum_x \frac{1}{d} \sum_{y\sim x} f(y)\, g(x)
\]](introgroupes110.png)
Sur un graphe fini, la théorie classique des chaînes de Markov (ou le
théorème de Perron-Frobenius) affirme que les valeurs propres de
l'opérateur h sont comprises entre 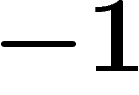 et
et  . Pour éviter les
problèmes de périodicité et d'oscillations causés par les valeurs propres
négatives, on considère une variante :
. Pour éviter les
problèmes de périodicité et d'oscillations causés par les valeurs propres
négatives, on considère une variante :
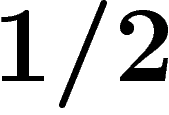 , soit reste sur
place, soit fait un pas de marche aléatoire.
, soit reste sur
place, soit fait un pas de marche aléatoire.
L'opérateur associé sur les fonctions sur le graphe est donc 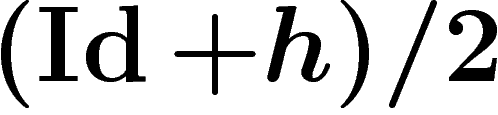 .
Abusons des notations et notons encore h cet opérateur, associé à la
marche aléatoire paresseuse (comme si à chaque sommet du graphe, on
ajoutait
.
Abusons des notations et notons encore h cet opérateur, associé à la
marche aléatoire paresseuse (comme si à chaque sommet du graphe, on
ajoutait 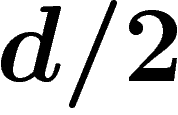 arêtes en boucle). Ses valeurs propres sont comprises
entre
arêtes en boucle). Ses valeurs propres sont comprises
entre  et
et  , le sous-espace propre associé à
, le sous-espace propre associé à  étant constitué des
fonctions constantes sur chaque composante.
étant constitué des
fonctions constantes sur chaque composante.
Pour deux mesures de probabilité 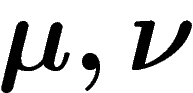 sur h, on note
sur h, on note
![\[\abs{\mu-\nu}=\frac12 \sum \abs{\mu(x)-\nu(x)}=\sup_{A\subset \Gamma}
\abs{\mu(A)-\nu(A)}\leq 1\]](introgroupes120.png)
En écrivant h (autoadjoint) dans une base diagonalisante, et en
utilisant l'inégalité de Cauchy-Schwarz 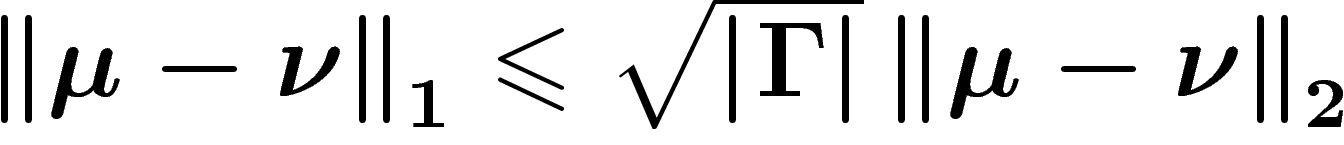 ,
on obtient :
,
on obtient :
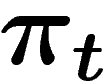 au temps t de la
marche aléatoire paresseuse partant d'un point quelconque converge vers
la mesure uniforme U sur la composante connexe du point de départ. De plus,
si
au temps t de la
marche aléatoire paresseuse partant d'un point quelconque converge vers
la mesure uniforme U sur la composante connexe du point de départ. De plus,
si 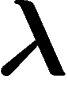 est la plus grande valeur propre de h inférieure à
est la plus grande valeur propre de h inférieure à  , on
a
, on
a
![\[
\abs{\pi_t-U}\leq \frac{\sqrt{\abs{\Gamma}}}{2}\, \lambda^t
\]](introgroupes125.png)
![\[
\tau \leq \frac{\frac12 \log{\abs{\Gamma}}+1}{-\log \lambda} \leq
\frac{\frac12 \log{\abs{\Gamma}}+1}{1-\lambda}
\]](introgroupes126.png)
Le temps de relaxation est, conventionnellement, le plus petit temps tel
que  .
.
La quantité 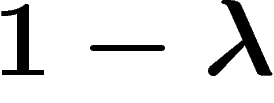 , première valeur propre non nulle du laplacien,
est appelée trou spectral du graphe ; plus il est grand, plus les
marches aléatoires convergent rapidement. L'évaluation du trou spectral
pour certains graphes définis par des actions de groupes de Kazhdan fait
l'objet de la section suivante.
, première valeur propre non nulle du laplacien,
est appelée trou spectral du graphe ; plus il est grand, plus les
marches aléatoires convergent rapidement. L'évaluation du trou spectral
pour certains graphes définis par des actions de groupes de Kazhdan fait
l'objet de la section suivante.
La connaissance de constantes de Kazhdan pour des systèmes générateurs d'un groupe permet de déduire des propriétés spectrales pour certains opérateurs agissant dans une représentation du groupe. Nous allons utiliser ce lien pour évaluer le trou spectral du laplacien d'un groupe de Kazhdan agissant sur certains graphes (cf. [HRV]).
Soient G un groupe, S un système générateur fini symétrique, et
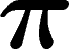 une représentation unitaire de G sur un Hilbert
une représentation unitaire de G sur un Hilbert 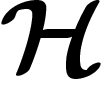 . Soit
. Soit
![\[
\kappa(\pi,S)=\inf_{\xi\in\H, \norm{\xi}=1} \max_{s\in S}
\norm{\pi(s)\xi-\xi}
\]](introgroupes131.png)
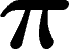 (qui ne peut
évidemment être non nulle que si
(qui ne peut
évidemment être non nulle que si 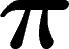 ne contient pas la représentation
identité).
ne contient pas la représentation
identité).
On définit de plus
![\[
h=\frac{1}{\abs{S}} \sum_{s\in S} \pi(s)\ \in L(\H)
\]](introgroupes134.png)
Par exemple, si 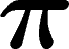 est la représentation régulière gauche de G,
alors h est simplement l'opérateur « moyenne sur les voisins » dans le
graphe de Cayley de G pour le système générateur S
(
est la représentation régulière gauche de G,
alors h est simplement l'opérateur « moyenne sur les voisins » dans le
graphe de Cayley de G pour le système générateur S
(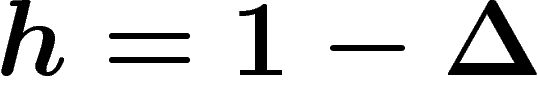 ).
).
On obtient dans ce cadre une évaluation du trou spectral du laplacien :
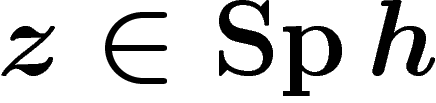 . Alors
. Alors ![\[\abs{z-1} \geq
\frac{\kappa(\pi,S)^2}{2\abs{S}}\]](introgroupes138.png)
En particulier, si G est un groupe de Kazhdan et 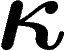 une constante
de Kazhdan par rapport à S, alors pour toute représentation unitaire de
G, le trou spectral de h est supérieur à
une constante
de Kazhdan par rapport à S, alors pour toute représentation unitaire de
G, le trou spectral de h est supérieur à 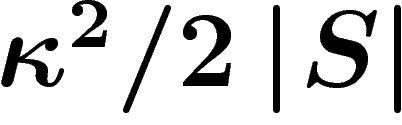 .
C'est cette propriété qui nous servira par la suite.
.
C'est cette propriété qui nous servira par la suite.
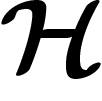 un espace de Hilbert,
un espace de Hilbert, 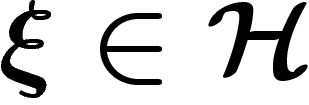 un vecteur normé. Soient
un vecteur normé. Soient
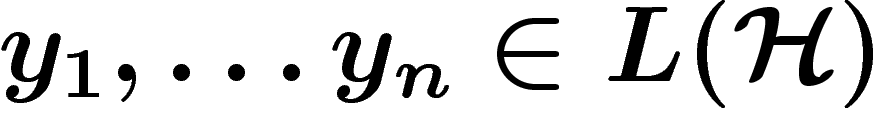 tous de norme inférieure ou égale à 1. On pose
tous de norme inférieure ou égale à 1. On pose
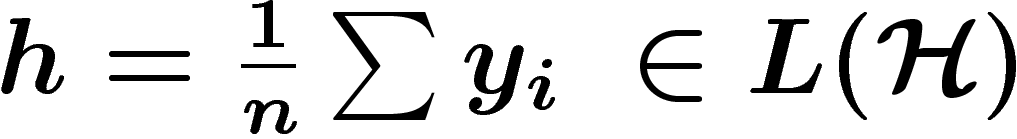 .
.
Si 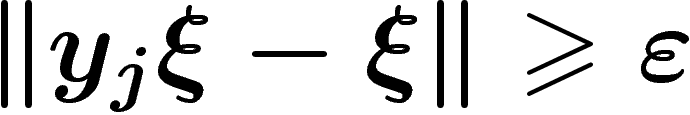 pour un certain
j, alors
pour un certain
j, alors 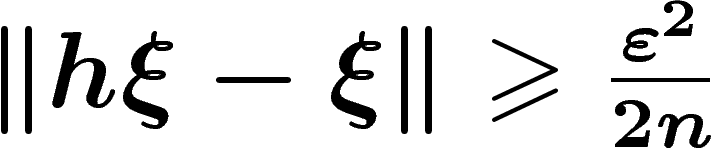 .
.
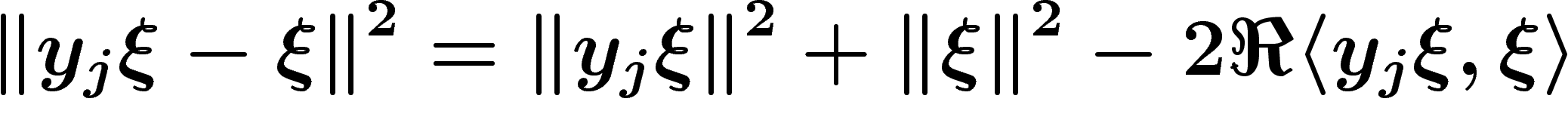 , on obtient que
, on obtient que  .
.
Par ailleurs, comme les 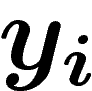 sont de norme inférieure à 1, on a
sont de norme inférieure à 1, on a 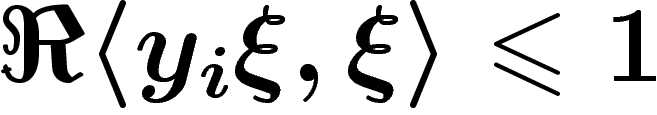 . Par conséquent,
. Par conséquent, 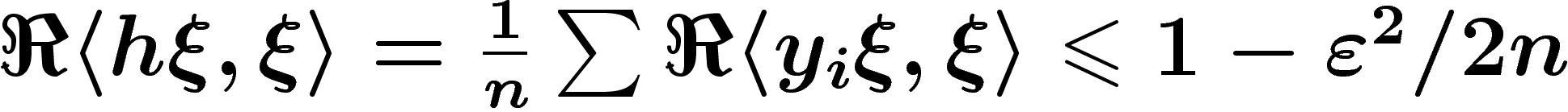 .
.
Pour tous 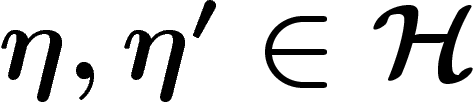 , on a
, on a  (évident sur un dessin).
Ceci donne
(évident sur un dessin).
Ceci donne 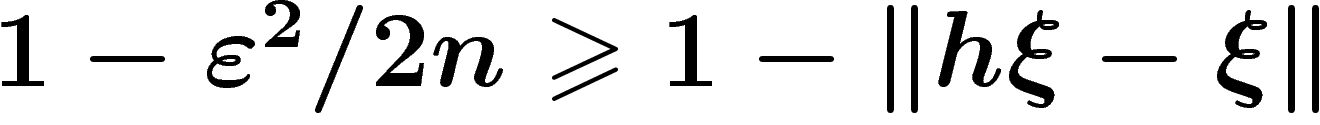 , d'où le lemme.
CQFD.
, d'où le lemme.
CQFD.
Revenons à la proposition. h est un opérateur hermitien sur 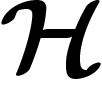 (car
S est symétrique et
(car
S est symétrique et  unitaire). On veut montrer que pour tout
unitaire). On veut montrer que pour tout 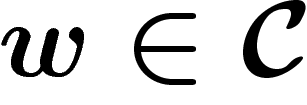 tel que
tel que 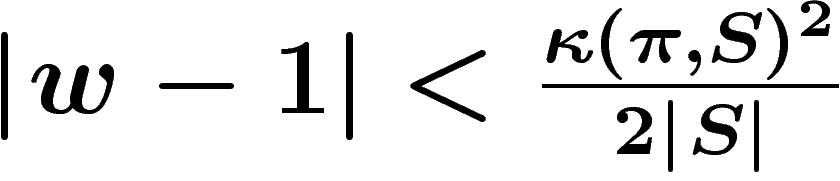 ,
,
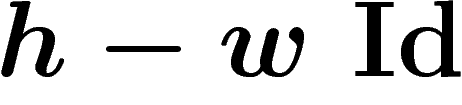 est inversible.
est inversible.
Soit 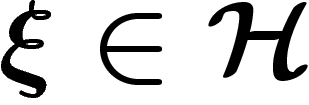 unitaire. Par définition de
unitaire. Par définition de 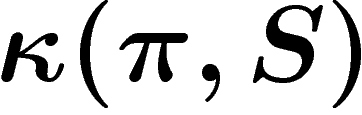 , il existe
un
, il existe
un 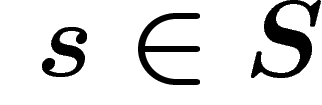 tel que
tel que 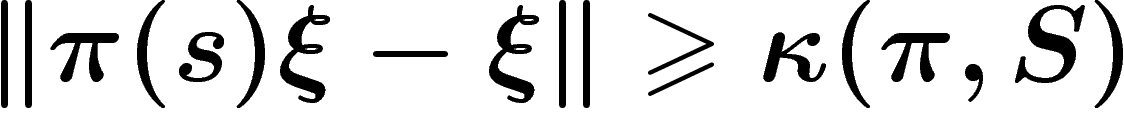 . Le lemme
implique alos que
. Le lemme
implique alos que 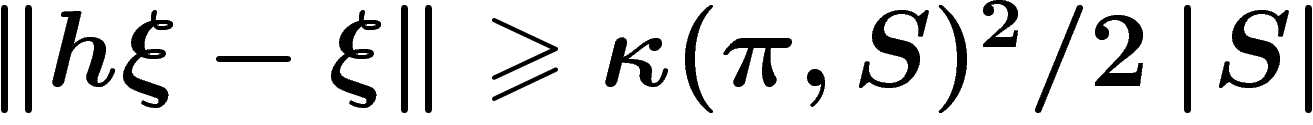 . Par conséquent,
. Par conséquent, 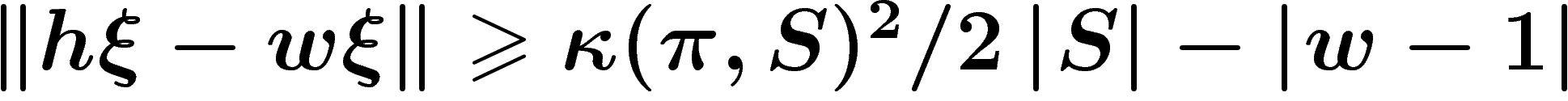 , ce qui suffit à montrer que l'opérateur
hermitien
, ce qui suffit à montrer que l'opérateur
hermitien 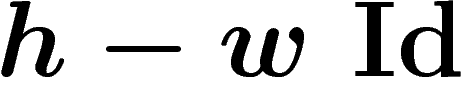 est inversible.
CQFD.
est inversible.
CQFD.
Un problème fréquemment rencontré en théorie algorithmique des groupes consiste à engendrer un élément aléatoire d'un groupe fini, selon la loi uniforme. Le but est de déterminer, par ordinateur, des propriétés d'un groupe donné comme une boîte noire : sont donnés un ensemble de générateurs du groupe et une fonction qui multiplie deux éléments. En outre, on sait dire si un élément est l'élément neutre. Disposer, dans un tel cadre, d'éléments aléatoires uniformément répartis dans le groupe permet de tester différentes propriétés (ordre...), et de répondre à des questions sur la nature du groupe donné, éventuellement avec une certaine probabilité d'erreur.
Le PRA (pour partial replacement algorithm) est un algorithme
heuristique destiné à produire de tels éléments aléatoires dans un groupe
fini G. L'idée est de partir d'un k-uplet générateur
 et de le transformer en un autre, en multipliant entre
eux des éléments du k-uplet. En répétant cette transformation un
nombre de fois assez grand, on espère aboutir à un k-uplet aléatoire
d'éléments du groupe.
et de le transformer en un autre, en multipliant entre
eux des éléments du k-uplet. En répétant cette transformation un
nombre de fois assez grand, on espère aboutir à un k-uplet aléatoire
d'éléments du groupe.
 d'un groupe fini
G. On lui applique itérativement la transformation suivante. À chaque étape, on choisit deux indices distincts
d'un groupe fini
G. On lui applique itérativement la transformation suivante. À chaque étape, on choisit deux indices distincts
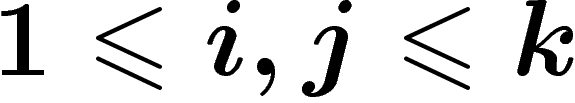 , et on multiplie, au choix,
, et on multiplie, au choix, 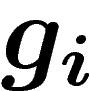 à droite ou à
gauche par
à droite ou à
gauche par 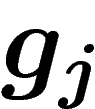 ou par
ou par 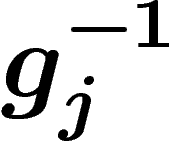 , avec égale probabilité, en laissant les
autres générateurs invariants.
, avec égale probabilité, en laissant les
autres générateurs invariants.
On a donc 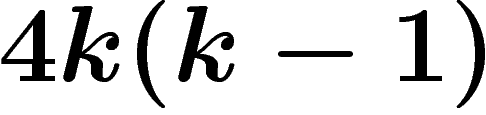 opérations de base :
opérations de base :
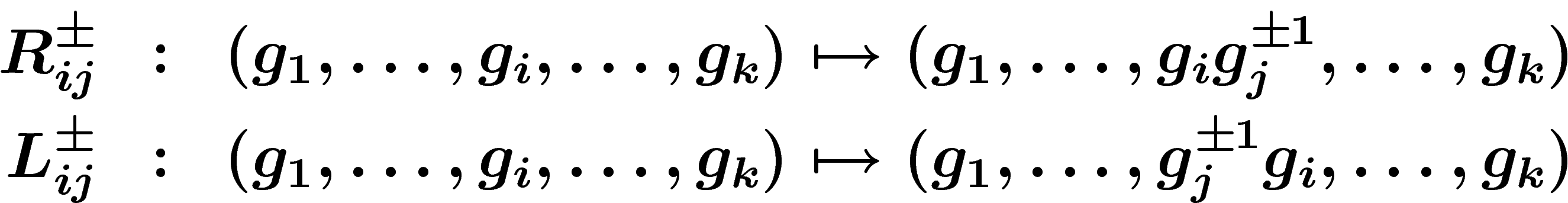
Notons que si l'on part d'un k-uplet générateur, on obtient encore un k-uplet générateur.
Ces opérations définissent un graphe 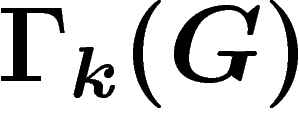 dont les sommets sont
tous les k-uplets générateurs de G, et dont les arêtes correspondent
aux mouvements de base. Le PRA est alors simplement la marche aléatoire
sur ce graphe.
dont les sommets sont
tous les k-uplets générateurs de G, et dont les arêtes correspondent
aux mouvements de base. Le PRA est alors simplement la marche aléatoire
sur ce graphe.
On appellera PRA paresseux l'algorithme consistant à suivre une marche aléatoire paresseuse dans ce graphe (ne rien faire la moitié du temps).
Maintenant, l'algorithme consiste à itérer un grand nombre de fois ces transformations, et à renvoyer un élément au hasard (mettons le premier) parmi le k-uplet obtenu.
Le premier problème qui se pose est celui de l'évaluation de la
convergence. D'après la proposition cvgraphes, on sait que la loi
du k-uplet obtenu au temps t converge exponentiellement vers la loi
uniforme sur les k-uplets générateurs situés dans la composante connexe
du k-uplet de départ. Il s'agit donc, d'une part, d'évaluer le trou
spectral du graphe 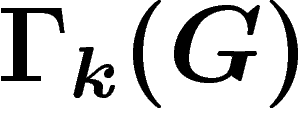 , pour connaître la vitesse de
convergence. Ce sera l'objet du théorème final, pour
G abélien. L'évaluation fera intervenir de manière cruciale la
propriété de Kazhdan de
, pour connaître la vitesse de
convergence. Ce sera l'objet du théorème final, pour
G abélien. L'évaluation fera intervenir de manière cruciale la
propriété de Kazhdan de 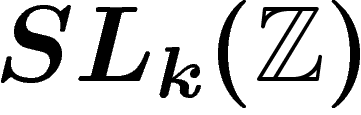 . D'autre part, reste un problème de
connexité. Une construction assez explicite (cf.[B]) montre que si
. D'autre part, reste un problème de
connexité. Une construction assez explicite (cf.[B]) montre que si
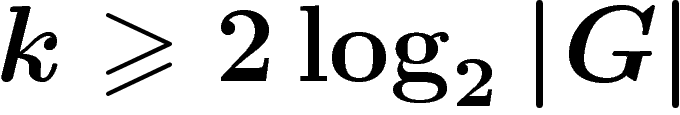 , le graphe du PRA est connexe : on peut passer
d'un k-uplet générateur à n'importe quel autre.
, le graphe du PRA est connexe : on peut passer
d'un k-uplet générateur à n'importe quel autre.
Le second problème est le suivant : on obtient, en sortie de l'algorithme, un k-uplet générateur uniformément choisi parmi tous les k-uplets générateurs de G. Il n'est pas sûr qu'en prenant un élément dans ce k-uplet, on obtienne un élément uniformément réparti dans G : la répartition des éléments composant un k-uplet générateur est biaisée. Par exemple, l'élément neutre apparaît moins souvent qu'un autre dans un k-uplet générateur pris au hasard.
Quantifions. Soit  l'ensemble des k-uplets générateurs de
G. Soient
l'ensemble des k-uplets générateurs de
G. Soient  la mesure de probabilité uniforme sur
la mesure de probabilité uniforme sur 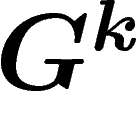 , et
, et 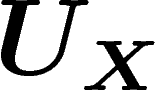 la mesure de probabilité uniforme sur X. Soit p la première
projection de
la mesure de probabilité uniforme sur X. Soit p la première
projection de 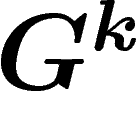 sur G, et soit
sur G, et soit 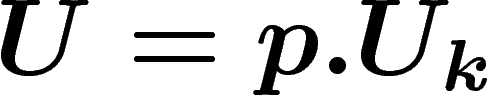 la mesure uniforme sur G. Si l'on attend assez longtemps, l'algorithme
rend un k-uplet générateur de loi
la mesure uniforme sur G. Si l'on attend assez longtemps, l'algorithme
rend un k-uplet générateur de loi 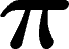 que l'on espère proche de
que l'on espère proche de
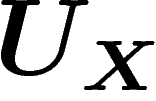 . En prenant au final le premier élément de ce k-uplet, on obtient
un élément distribué selon
. En prenant au final le premier élément de ce k-uplet, on obtient
un élément distribué selon 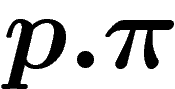 . Alors :
. Alors :
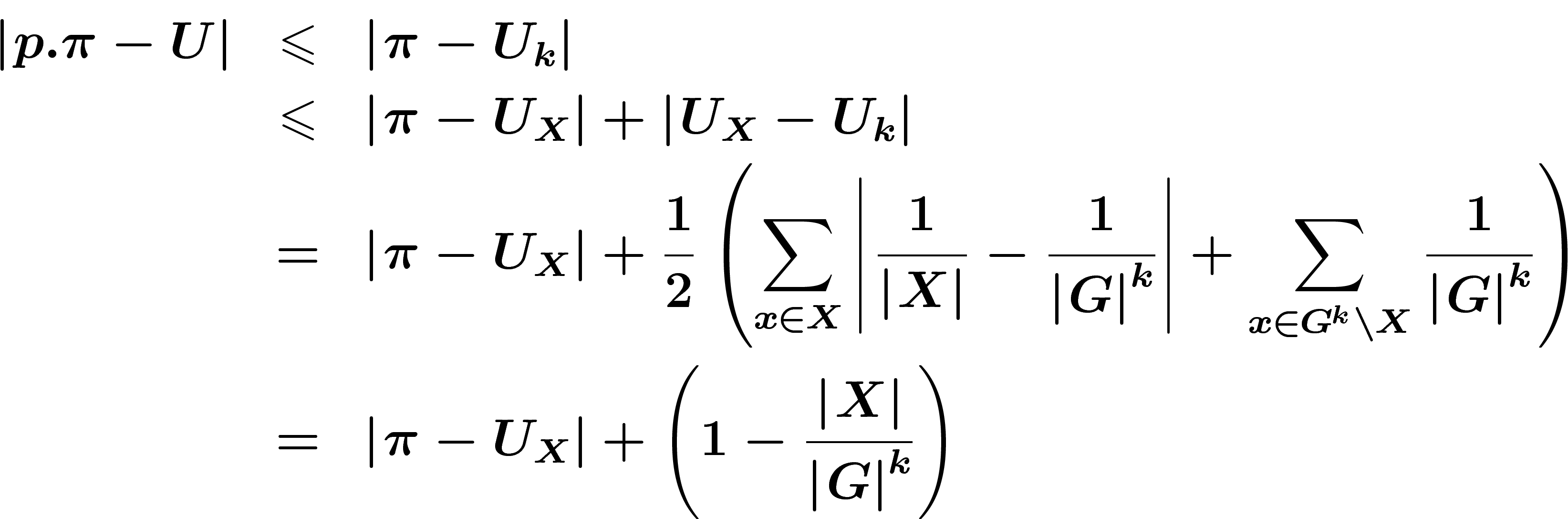
Le problème est donc d'évaluer la proportion de k-uplets qui sont générateurs. Donnons une évaluation très simple, qui peut être raffinée :
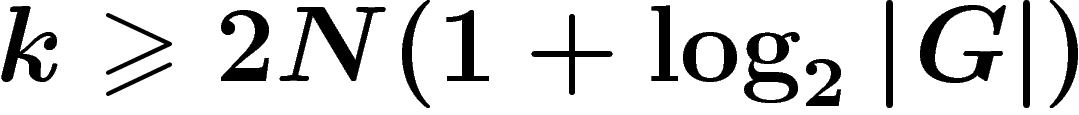 , alors un k-uplet d'éléments de G
choisi au hasard est générateur avec probabilité supérieure à
, alors un k-uplet d'éléments de G
choisi au hasard est générateur avec probabilité supérieure à 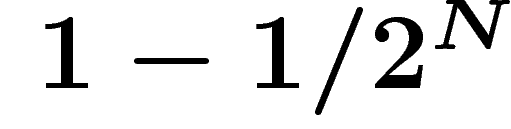 (N est un entier).
(N est un entier).
 sont des éléments de G qui engendrent
un sous-groupe
sont des éléments de G qui engendrent
un sous-groupe 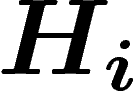 non égal à G, un élément pris au hasard dans G
appartient donc à
non égal à G, un élément pris au hasard dans G
appartient donc à 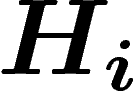 avec probabilité inférieure à
avec probabilité inférieure à 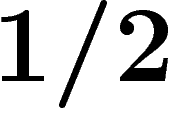 . En ajoutant
un élément au hasard à un tel système, on passe donc à un sur-groupe
. En ajoutant
un élément au hasard à un tel système, on passe donc à un sur-groupe
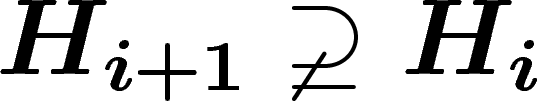 avec probabilité supérieure à
avec probabilité supérieure à 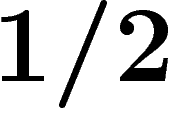 . Le
cardinal de
. Le
cardinal de 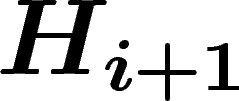 est, pour la même raison, au moins le double de celui de
est, pour la même raison, au moins le double de celui de 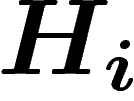 .
.
Par conséquent, en prenant des éléments au hasard, avec probabilité
supérieure à 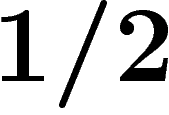 à chaque étape on double au moins la taille du
sous-groupe engendré, tant qu'on n'a pas atteint tout G. Si on tire k
éléments, il suffit donc de faire
à chaque étape on double au moins la taille du
sous-groupe engendré, tant qu'on n'a pas atteint tout G. Si on tire k
éléments, il suffit donc de faire 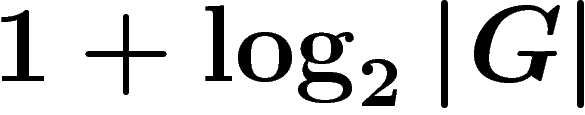 bons tirages parmi ces
k. Si
bons tirages parmi ces
k. Si 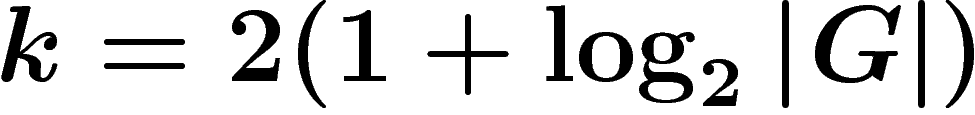 , la probabilité d'avoir fait
, la probabilité d'avoir fait
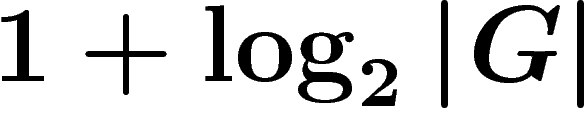 bons tirages est supérieure à
bons tirages est supérieure à 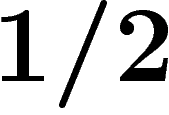 . En faisant
. En faisant
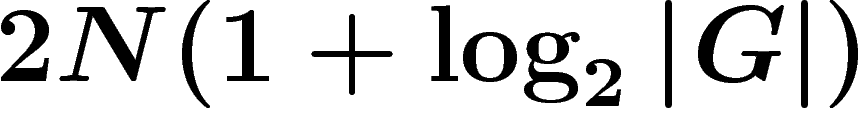 tirages, la probabilité de ne pas avoir fait assez
de bons tirages est inférieure à
tirages, la probabilité de ne pas avoir fait assez
de bons tirages est inférieure à 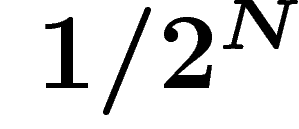 , d'où le résultat.
CQFD.
, d'où le résultat.
CQFD.
La même veine de raisonnement montre aussi qu'un système générateur
minimal de G ne peut pas avoir plus de 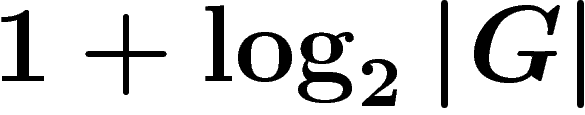 éléments.
éléments.
Reste donc le problème de la convergence vers l'équilibre du PRA, qui est traité ensuite dans le cas des groupes abéliens.
On va exploiter la propriété de Kazhdan d'un certain groupe agissant sur le graphe du PRA pour en déduire une minoration du trou spectral de ce graphe.
La remarque fondamentale est qu'un mouvement de base du PRA correspond à
un automorphisme du groupe libre à k éléments. Ainsi, on peut faire
agir un sous-groupe A de 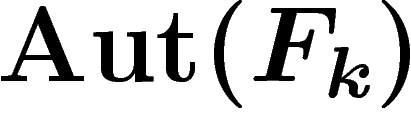 sur le graphe
sur le graphe 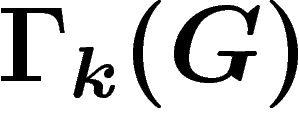 des
k-uplets générateurs du groupe G considéré. Si le sous-groupe A est
de Kazhdan, alors d'après les raisonnements ci-dessus, on pourra
contrôler la vitesse de convergence de la marche aléatoire sur
des
k-uplets générateurs du groupe G considéré. Si le sous-groupe A est
de Kazhdan, alors d'après les raisonnements ci-dessus, on pourra
contrôler la vitesse de convergence de la marche aléatoire sur
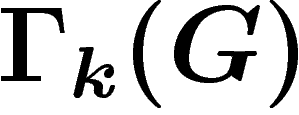 .
.
Malheureusement, on ne sait pas si 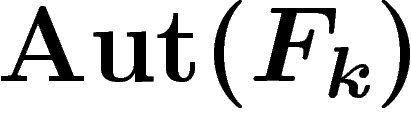 est de Kazhdan. Cependant,
si le groupe G est commutatif, l'action se factorise en une action de
est de Kazhdan. Cependant,
si le groupe G est commutatif, l'action se factorise en une action de
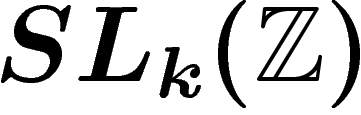 , qui, lui, est de Kazhdan pour
, qui, lui, est de Kazhdan pour 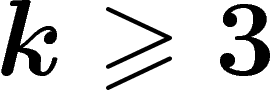 . C'est le résultat
que nous énoncerons.
. C'est le résultat
que nous énoncerons.
Explicitons. Considérons par exemple le mouvement 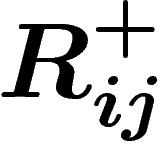 du PRA qui
passe de
du PRA qui
passe de 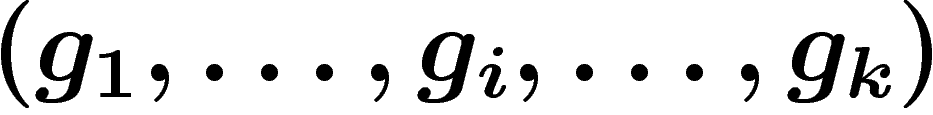 à
à 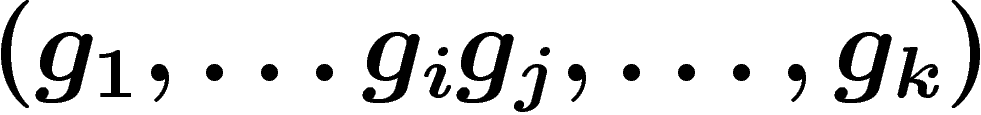 . On lui associe un morphisme
. On lui associe un morphisme 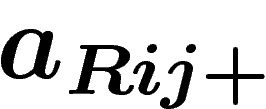 de
de 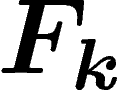 dans
lui-même de la manière suivante : si
dans
lui-même de la manière suivante : si 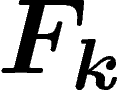 est engendré par
est engendré par
 , le morphisme est celui qui associe
, le morphisme est celui qui associe 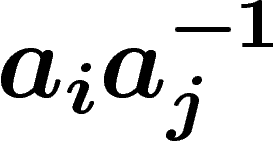 à
à 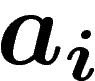 et
laisse invariants les autres générateurs (on met un inverse pour obtenir
une action à gauche plus tard). Comme le k-uplet obtenu est à
nouveau générateur, ce morphisme est bijectif.
et
laisse invariants les autres générateurs (on met un inverse pour obtenir
une action à gauche plus tard). Comme le k-uplet obtenu est à
nouveau générateur, ce morphisme est bijectif.
Maintenant, soit 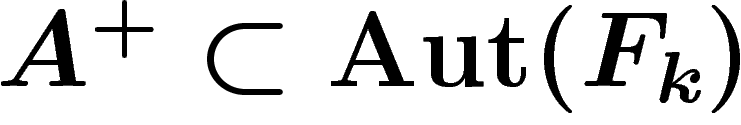 le sous-groupe engendré par ces
automorphismes. On considère un groupe fini G, ainsi que le graphe
le sous-groupe engendré par ces
automorphismes. On considère un groupe fini G, ainsi que le graphe
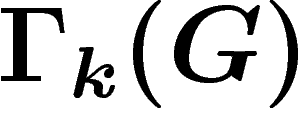 associé. Chaque arête de ce graphe correspond à un mouvement
du PRA, définissant lui-même un élément
associé. Chaque arête de ce graphe correspond à un mouvement
du PRA, définissant lui-même un élément 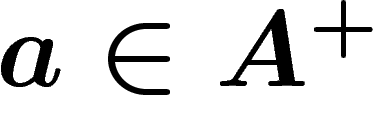 . Ceci définit une
action des générateurs de
. Ceci définit une
action des générateurs de 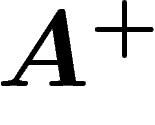 sur le graphe
sur le graphe 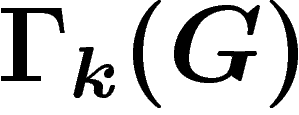 , consistant,
pour un générateur, à suivre les arêtes correspondantes.
, consistant,
pour un générateur, à suivre les arêtes correspondantes.
Vérifions que suivre deux arêtes de suite revient bien à composer les
automorphismes de 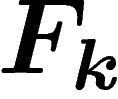 associés à ces arêtes. En termes plus
algébriques, un k-uplet générateur de G est un morphisme surjectif de
associés à ces arêtes. En termes plus
algébriques, un k-uplet générateur de G est un morphisme surjectif de
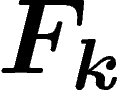 sur G,
sur G,  s'identifiant à
s'identifiant à 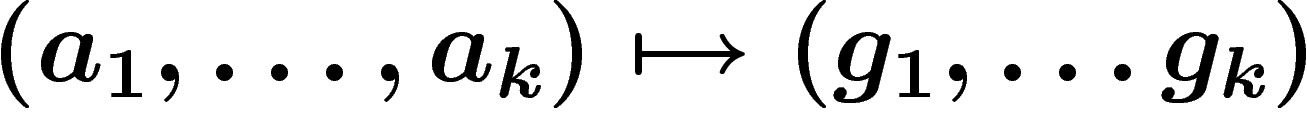 .
. 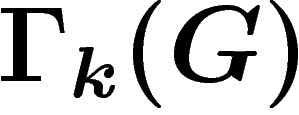 s'identifie donc à
s'identifie donc à
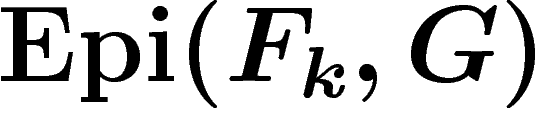 . De plus
. De plus 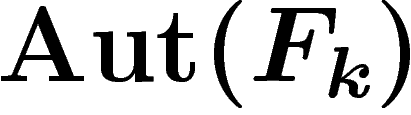 agit sur
agit sur 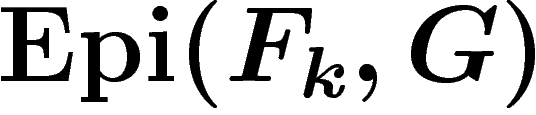 par
par
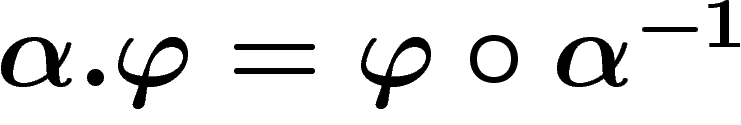 , pour
, pour 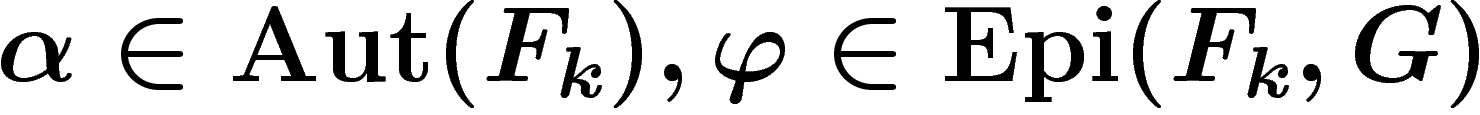 : c'est bien une action à gauche, respectant la
composition. Les mouvements du PRA correspondent, pour cette
action, à des éléments
: c'est bien une action à gauche, respectant la
composition. Les mouvements du PRA correspondent, pour cette
action, à des éléments  de
de 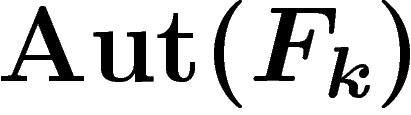 , explicités
ci-dessus, qui engendrent un sous-groupe
, explicités
ci-dessus, qui engendrent un sous-groupe 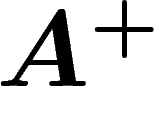 .
.
Cette action de 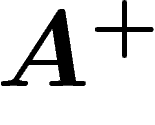 sur le graphe
sur le graphe 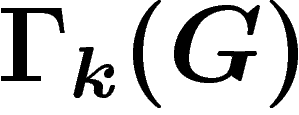 se transpose
directement en une représentation de
se transpose
directement en une représentation de 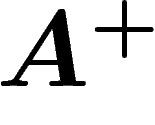 dans
dans 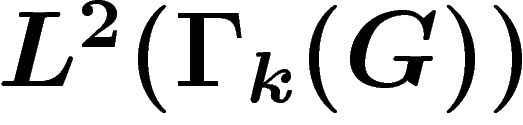 par
par
 . Chaque mouvement du PRA étant
inversible, l'action est bijective sur les points du graphe, et donc cette
représentation est isométrique.
. Chaque mouvement du PRA étant
inversible, l'action est bijective sur les points du graphe, et donc cette
représentation est isométrique.
Par définition, l'action 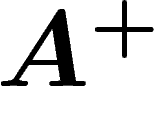 est transitive sur chacune des composantes
connexes de
est transitive sur chacune des composantes
connexes de 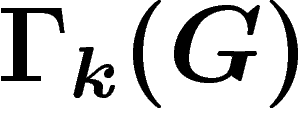 . Une fonction de
. Une fonction de 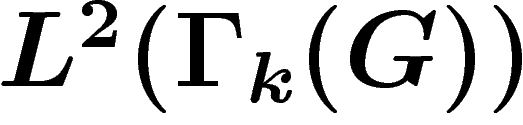 ne peut
donc être invariante que si elle est constante sur chaque composante
connexe.
ne peut
donc être invariante que si elle est constante sur chaque composante
connexe.
On se restreint désormais à une composante connexe C de 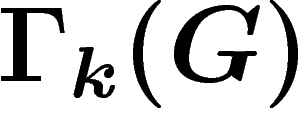 .
De plus, on s'intéresse à
.
De plus, on s'intéresse à 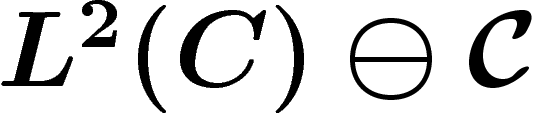 , i.e. on enlève les
fonctions constantes (ou encore, on se restreint aux fonctions de moyenne
nulle). Ceci nous laisse une représentation de
, i.e. on enlève les
fonctions constantes (ou encore, on se restreint aux fonctions de moyenne
nulle). Ceci nous laisse une représentation de 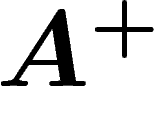 sans vecteurs
invariants.
sans vecteurs
invariants.
Soit 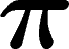 cette représentation. Soit
cette représentation. Soit 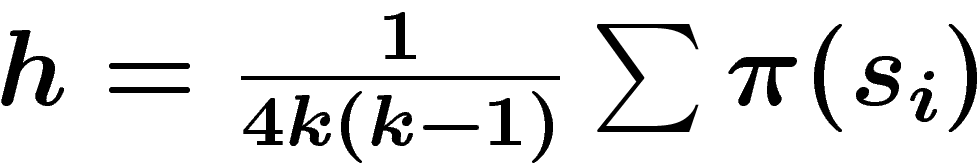 défini comme à la section Tspec. Soit
défini comme à la section Tspec. Soit 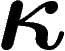 la constante de
Kazhdan de
la constante de
Kazhdan de 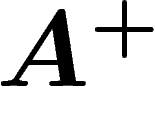 . Si
. Si 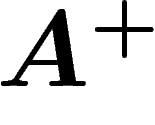 est de Kazhdan, on a
est de Kazhdan, on a 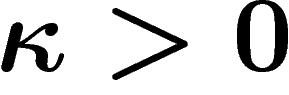 .
.
La proposition de la section Tspec donne alors que les valeurs
propres de h sont éloignées de 1 d'au moins 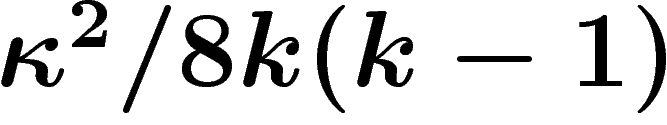 . Or,
comme les arêtes du graphe correspondent exactement aux générateurs
. Or,
comme les arêtes du graphe correspondent exactement aux générateurs
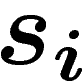 de
de 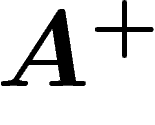 , l'opérateur h n'est autre que l'opérateur de la marche
aléatoire sur le graphe. En passant à la marche aléatoire paresseuse pour
éviter les problèmes d'oscillation, et en reprenant les notations
ci-dessus pour le PRA, on a donc démontré que :
, l'opérateur h n'est autre que l'opérateur de la marche
aléatoire sur le graphe. En passant à la marche aléatoire paresseuse pour
éviter les problèmes d'oscillation, et en reprenant les notations
ci-dessus pour le PRA, on a donc démontré que :
![\[
\abs{\pi_t-U} \leq \abs{G}^{k/2}\,\left(1-\frac{\kappa^2}{16k(k-1)}\right)^t
\]](introgroupes260.png)
Fort malheureusement, on ne sait pas si le groupe 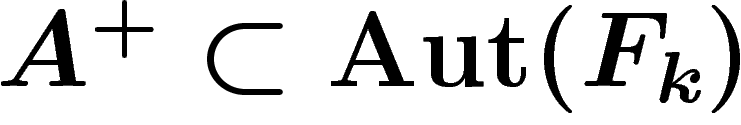 ainsi défini est de Kazhdan.
ainsi défini est de Kazhdan.
Par contre, ce raisonnement se transpose dans le cas où le groupe G
est abélien, en remplaçant le groupe libre 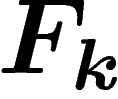 par son analogue abélien
par son analogue abélien
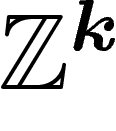 . Dans ce cas, on a
. Dans ce cas, on a 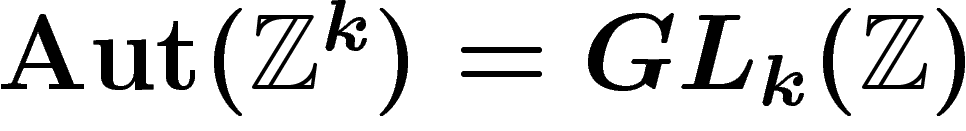 .
.
Alors le groupe 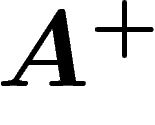 est remplacé par
est remplacé par 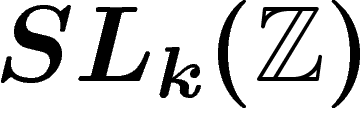 . En effet, sur
. En effet, sur 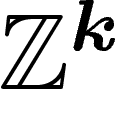 ,
un mouvement du PRA revient à ajouter (ou soustraire) le j-ième
générateur au i-ième ; la matrice d'une telle transformation linéaire
de
,
un mouvement du PRA revient à ajouter (ou soustraire) le j-ième
générateur au i-ième ; la matrice d'une telle transformation linéaire
de 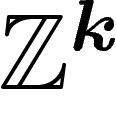 est la diagonale plus un 1 en position
est la diagonale plus un 1 en position 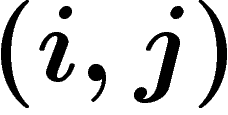 . Ces telles matrices
engendrent
. Ces telles matrices
engendrent 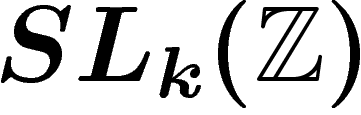 .
.
Or ce groupe est de Kazhdan pour 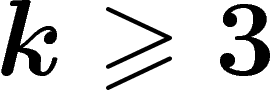 . Mieux, on connaît
(théorème sh) une estimation de la constante de Kazhdan
. Mieux, on connaît
(théorème sh) une estimation de la constante de Kazhdan 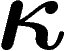 pour ce
système de générateurs : il existe une constante C telle que
pour ce
système de générateurs : il existe une constante C telle que
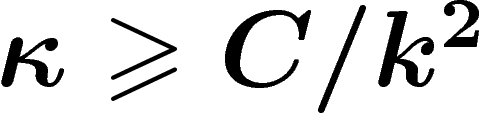 pour
pour 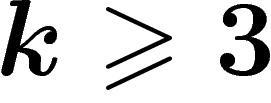 .
.
On a ainsi démontré :
 ,
, 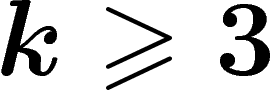 , et soit
, et soit 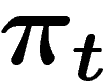 la
loi du k-uplet générateur obtenu par application de t étapes du PRA
paresseux.
Soit U la mesure uniforme sur la composante connexe de
la
loi du k-uplet générateur obtenu par application de t étapes du PRA
paresseux.
Soit U la mesure uniforme sur la composante connexe de
 dans le graphe du PRA. Il existe une constante C
indépendante de G et k telle que
dans le graphe du PRA. Il existe une constante C
indépendante de G et k telle que
![\[
\abs{\pi_t-U} \leq \abs{G}^{k/2}\, \left(1-\frac{C}{k^6}\right)^t
\]](introgroupes279.png)
En particulier, le temps de relaxation est de l'ordre de 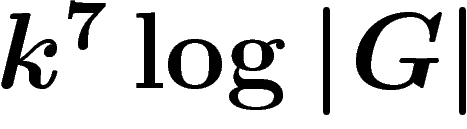 .
.
Le principal point à noter est la dépendance logarithmique en 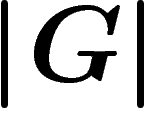 du temps de relaxation. L'exposant de k n'est pas optimal.
L'évaluation croît avec k, ce qui est normal puisqu'on demande la
convergence dans un graphe plus grand.
du temps de relaxation. L'exposant de k n'est pas optimal.
L'évaluation croît avec k, ce qui est normal puisqu'on demande la
convergence dans un graphe plus grand.
Enfin, la restriction à une composante connexe peut être contournée quand
on sait (cf. [B]) que pour 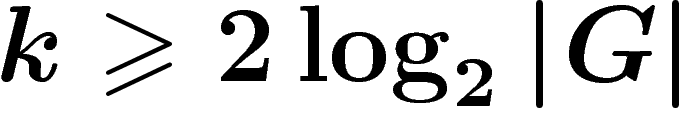 , le graphe du PRA
est connexe.
, le graphe du PRA
est connexe.
[B] L. Babai, Randomization in group algorithms: conceptual questions, in Groups and computation II, édité par L. Finkelstein et W. M. Kantor, DIMACS series 28, AMS, Providence, 1997.
[GH] Sur les Groupes hyperboliques d'après Mikhael Gromov, édité par É. Ghys et P. de la Harpe, Progress in Math. 83, Birkhäuser, Boston (1990).
[Gr] M. Gromov, Hyperbolic groups, in Essays in group theory, édité par S. M. Gersten, M.S.R.I. Publ. 8, Springer (1987), p. 75--263.
[HV] P. de la Harpe, A. Valette, La propriété (T) de Kazhdan pour les groupes localement compacts, Astérisque 175, SMF (1989).
[HRV] P. de la Harpe, A. G. Robertson, A.Valette, On the spectrum of the sum of generators for a finitely generated group, Israel J. Math. 81 (1993), p. 65--96.
[Sh] Y. Shalom, Bounded generation and Kazhdan's property (T), Publ. Math. IHÉS 90 (1999), p. 145--168.