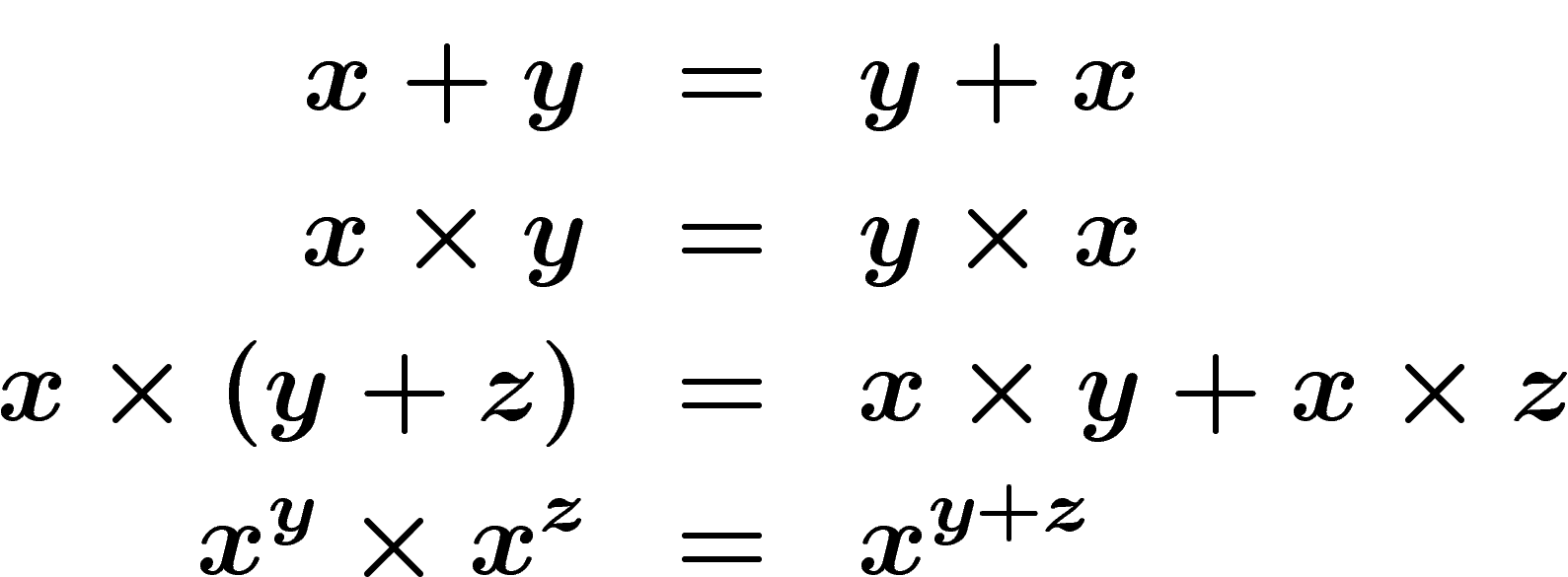
Ce texte se veut une introduction grand public aux problèmes mathématiques sur lesquels j'ai travaillé durant ma thèse : les groupes aléatoires. Il a été conçu comme un exposé à donner au Palais de la Découverte.
Tous les collégiens ont appris à manipuler les nombres et les expressions mathématiques selon certaines règles. Vous utilisez tous, consciemment ou sans s'en apercevoir, des règles telles que :
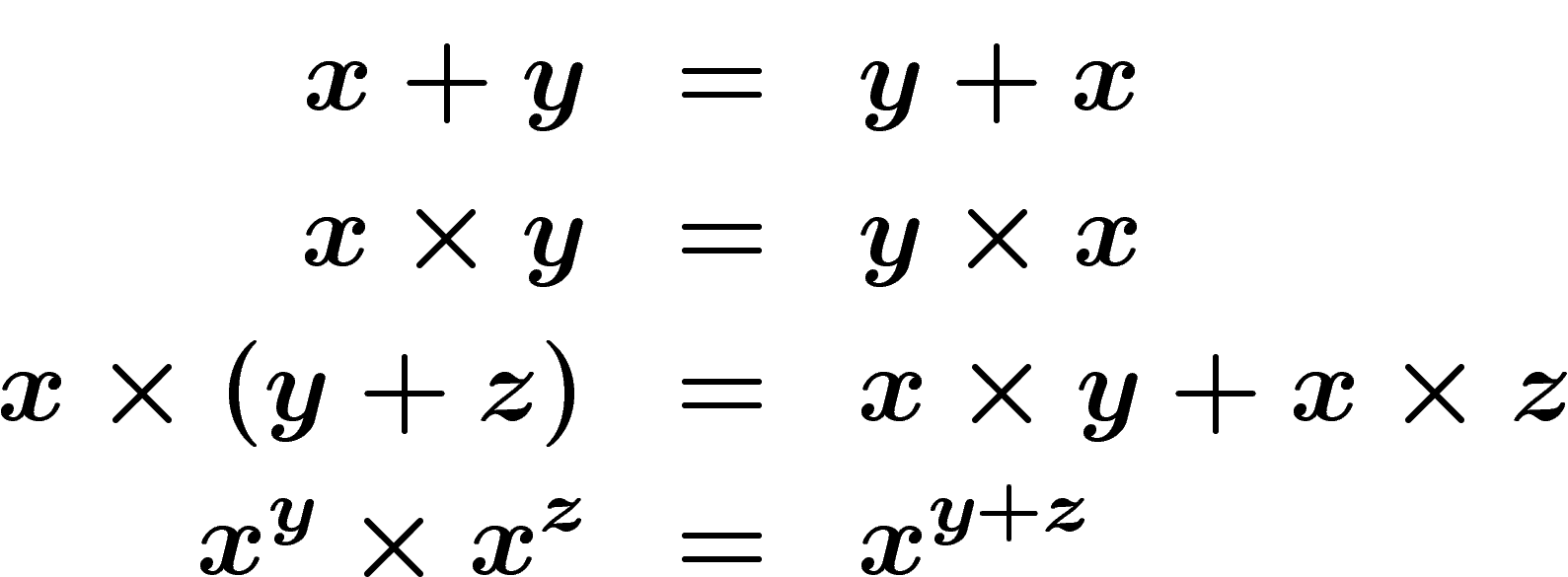
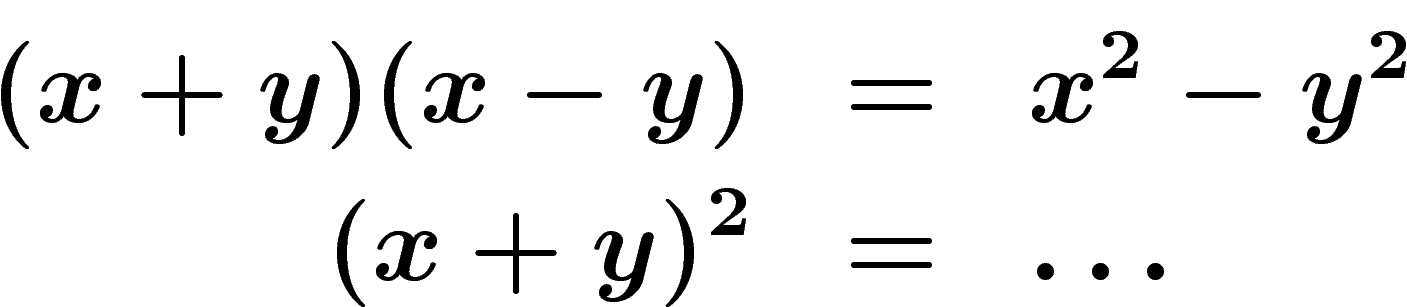
Dans cet exposé, je tenterai de montrer ce qui se passe si on se révolte contre ces règles et qu'on essaie d'en choisir d'autres qui nous plaisent plus. Je montrerai qu'on peut obtenir un calcul cohérent, souvent avec de jolies interprétations géométriques. A la fin de l'exposé, je regarderai ce qui se passe si on se donne des règles de calcul complètement au hasard.
Le monde dans lequel on va vivre sera le monde des "jeux de mots". Pour faire des jeux de mots, il faut avoir des lettres. On se donnera, mettons, deux lettres de base a et b. On va travailler avec tous les mots qu'on peut écrire avec des a et des b, par exemple : aabbab ou encore abbabaab.
Jusqu'ici, ce n'est pas très intéressant. Maintenant, se donner des
règles de calcul, c'est se donner des égalités entre mots. Par exemple,
on peut décider que 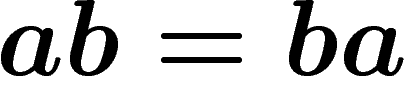 . Cela veut dire que chaque fois que, dans un
mot, on voit apparaître un a suivi d'un b, on peut remplacer ab par
ba,
et inversement. Un exemple de tel calcul avec cette règle :
. Cela veut dire que chaque fois que, dans un
mot, on voit apparaître un a suivi d'un b, on peut remplacer ab par
ba,
et inversement. Un exemple de tel calcul avec cette règle :
Partons du mot abbabaab.
en 3e et 4e position on voit apparaître ba
on a le droit de remplacer par ab
on obtient le mot ababbaab
maintenant, en 5e et 6e position on a un autre ba
on peut le remplacer par ab
on obtient le mot abababab
Conclusion : dans le jeu de mots avec la règle 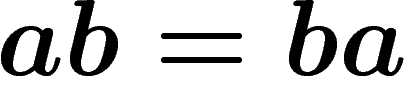 les mots
abbabaab et abababab sont égaux !
les mots
abbabaab et abababab sont égaux !
Pourquoi appeler cela des "jeux de mots" ? Le jeu est le suivant : Je vous donne deux mots, je vous donne des règles de calcul. Je vous demande de prouver que les deux mots sont égaux en utilisant les règles de calcul.
Voici un autre exemple de jeu de mots :
Cette fois-ci on prend trois lettres 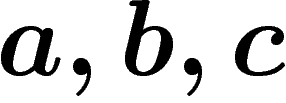 . On se donne les règles suivantes :
. On se donne les règles suivantes :
 et
et 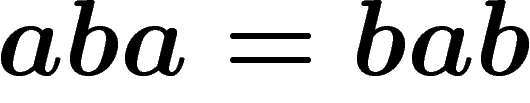 et
et 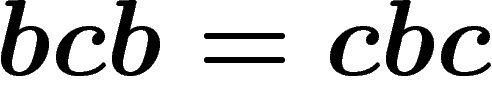
Pouvez-vous me dire si abacaba est égal à bcbabcb avec ces règles ? Solution
Pouvez-vous me dire si acabbc est égal à cabbc avec ces règles ? Indice
Revenons au jeu de mots ou la seule règle est 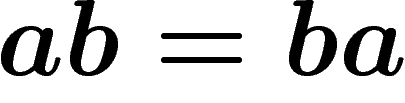 . En prenant un mot
quelconque comme abbabbaba, et en jouant avec la règle, on s'aperçoit
vite qu'on peut échanger les a et les b comme on veut. On peut, par
exemple, mettre tous les a à gauche et les b à droite :
. En prenant un mot
quelconque comme abbabbaba, et en jouant avec la règle, on s'aperçoit
vite qu'on peut échanger les a et les b comme on veut. On peut, par
exemple, mettre tous les a à gauche et les b à droite :
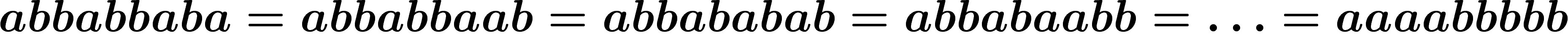
Cela veut dire que dans le jeu 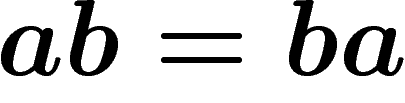 tous les mots sont égaux à un mot
de la forme
tous les mots sont égaux à un mot
de la forme 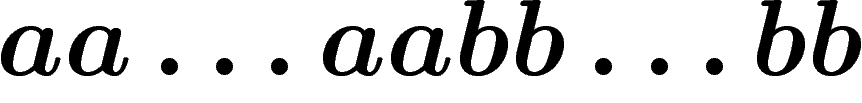 . Le nombre de a dans cette
écriture est le même que le nombre de a dans le mot initial, et c'est
pareil pour le nombre de b.
. Le nombre de a dans cette
écriture est le même que le nombre de a dans le mot initial, et c'est
pareil pour le nombre de b.
Dans le jeu 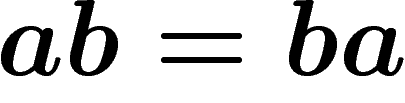 , tout ce qui compte est donc le nombre de a et de
b dans le mot initial !
, tout ce qui compte est donc le nombre de a et de
b dans le mot initial !
Mais est-ce que c'est vraiment _tout_ ce qui compte ? Est-ce que des mots
avec un nombre différent de a et de b sont vraiment inégaux avec nos
règles, c'est-à-dire qu'on ne pourra jamais passer de l'un à l'autre ? On
peut voir que oui : la seule règle disponible est 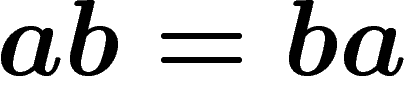 elle ne change
pas le nombre de a et de b. Donc, même si on pouvait tester toutes
les manières d'appliquer la règle, on n'arriverait jamais à changer le
nombre de a et de b.
elle ne change
pas le nombre de a et de b. Donc, même si on pouvait tester toutes
les manières d'appliquer la règle, on n'arriverait jamais à changer le
nombre de a et de b.
Cela veut dire qu'on a complèteme résolu le jeu initial 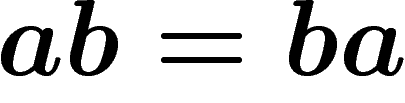 ! Tous
les mots se mettent sous la forme
! Tous
les mots se mettent sous la forme 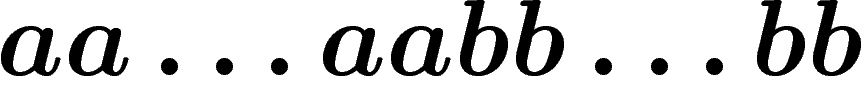 .
.
On peut représenter ces mots sur une grille dans un quart de plan. Une barre horizontale de la grille correspond à ajouter un a, une barre verticale correspond à ajouter un b. [dessin de la grille dans un quart de plan au tableau]
Sur ce dessin, on peut même lire graphiquement notre règle 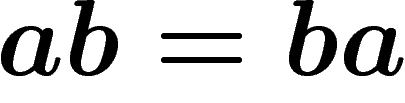 :
faire ab, c'est se déplacer d'une unité horizontalement puis d'une
unité verticalement, et faire ba, c'est se déplacer verticalement puis horizontalement, et ça nous mène au même endroit sur la grille !
:
faire ab, c'est se déplacer d'une unité horizontalement puis d'une
unité verticalement, et faire ba, c'est se déplacer verticalement puis horizontalement, et ça nous mène au même endroit sur la grille !
Le jeu 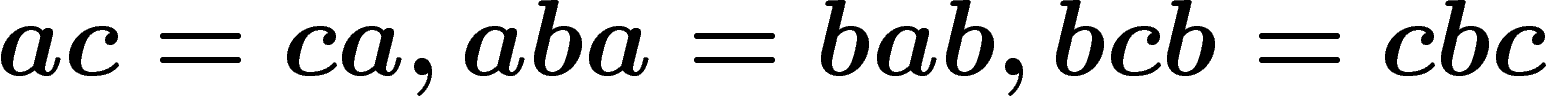 a aussi une interprétation géométrique,
en termes de tresses (allez voir sur le site d'Animath pour une
introduction aux
tresses).
a aussi une interprétation géométrique,
en termes de tresses (allez voir sur le site d'Animath pour une
introduction aux
tresses).
C'est un jeu de mots à trois lettres 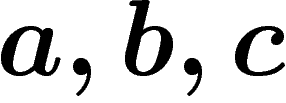 , les règles sont :
, les règles sont :
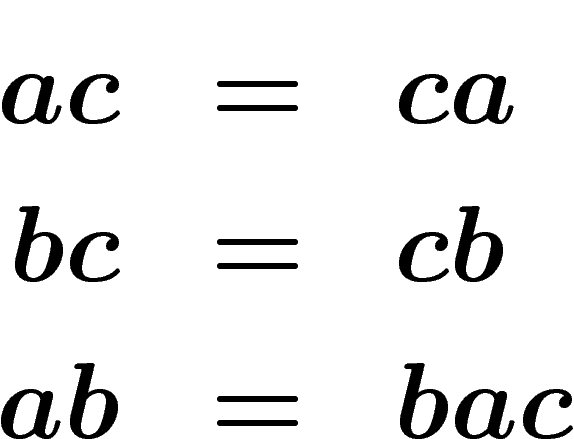
Pouvez-vous prouver que 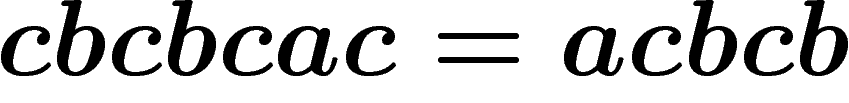 ?
Solution
?
Solution
On va maintenant étendre légèrement ces règles de calcul : on va se donner le droit d'écrire des mots qui contiennent des des anti-a, des anti-b et des anti-c qui nous permettent d'annuler un a, un b ou un c.
Les anti-a seront notés 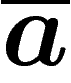 , les anti-b,
, les anti-b, 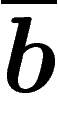 , et les anti-c,
, et les anti-c,  .
.
Autrement dit, on introduit les nouvelles règles 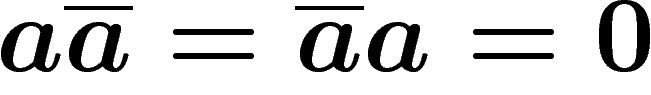 ,
, 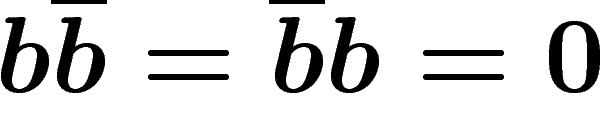 , etc
(0 représente un mot vide).
, etc
(0 représente un mot vide).
Cela veut dire que dans un mot, on a le droit de supprimer dès que 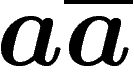 ou
ou
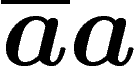 apparaît. Inversement, on a le droit de faire apparaître un
apparaît. Inversement, on a le droit de faire apparaître un 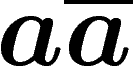 ou un
ou un
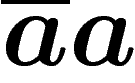 à partir de rien si cela nous arrange pour la suite.
à partir de rien si cela nous arrange pour la suite.
On obtient ainsi ce que les mathématiciens appellent un groupe. Les groupes, où on peut annuler les lettres, sont souvent plus commodes que les jeux de mots sans anti-lettres.
Question à la salle : que doit-on faire si on veut trouver l'anti-mot d'un mot tel que abcbac ? Suffit-il de mettre des barres sur toutes les lettres ?
Dans l'exemple géométrique des tresses développé ci-dessus (pour ceux
quiont suivi le lien),
on a vu que dans ce jeu, a, b et c pouvaient être interprétés comme des
croisements de brins. Maintenant, que sont des anti-lettres et des
anti-mots ? Ce sont simplement les mots qui sont des "images miroirs" des
autres croisements. Cette visualisation permet des preuves plus rapides :
par exemple, prouvez que 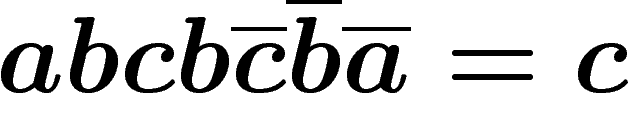 dans ce jeu ? Indice : faites un
dessin !
dans ce jeu ? Indice : faites un
dessin !
Pour ceux qui n'ont pas regardé les tresses on peut revenir à 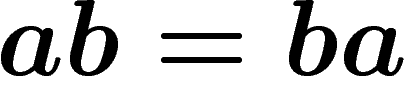 : introduire
les anti-lettres permet de compléter le quart de grille en la grille, et
tout ce qui compte dans ce jeu, c'est le nombre de a et de b, où on
compte négativement les
: introduire
les anti-lettres permet de compléter le quart de grille en la grille, et
tout ce qui compte dans ce jeu, c'est le nombre de a et de b, où on
compte négativement les 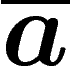 et les
et les 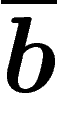 (attention dans ce cas, montrer que
les
(attention dans ce cas, montrer que
les 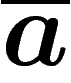 et les
et les 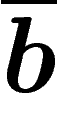 commutent aussi n'est pas immédiat... on peut partir de
commutent aussi n'est pas immédiat... on peut partir de
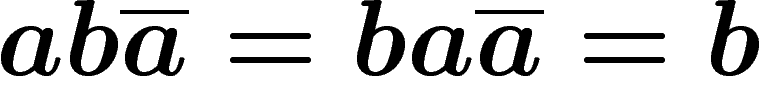 , donc on a le droit de réutiliser
, donc on a le droit de réutiliser 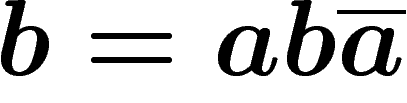 , ensuite on a
, ensuite on a
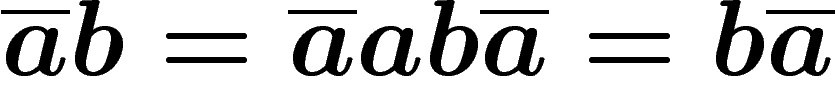 donc
donc 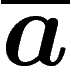 commute avec b, de même pour les autres
etc.).
commute avec b, de même pour les autres
etc.).
Maintenant, on peut se demander si avec des règles données, il est
possible de réduire n'importe quel mot à rien. Par exemple, si on donne
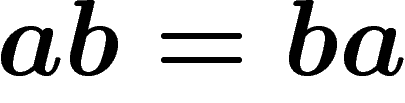 et
et 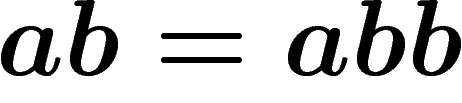 et
et 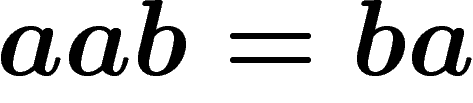 , on va avoir :
, on va avoir :
![\[a=ab\b=abb\b=ab=\a aab=\a ba=\a ab=b\]](ga_palaisdecouverte048.png)
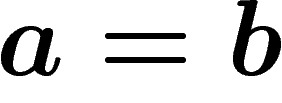 :
:
![\[b=\b \b bbb=\b \b aab=\b \b ba=\b a=\b b=0\]](ga_palaisdecouverte050.png)
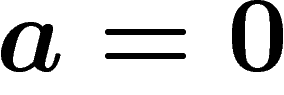 .
.
Si on se donne beaucoup de règles, on va donc facilement tomber sur des groupes où, en fait, il n'y a rien à dire car tous les mots s'annulent !
Un théorème récent permet de préciser cette idée. C'est un théorème qui explique ce qui se passe lorsqu'on choisit beaucoup de règles que l'on tire au hasard. Si on en prend plus qu'un certain seuil, on obtiendra très probablement que tout mot s'annule. Si on en prend moins que ce seuil, on obtiendra qu'il y a des mots qui se s'annulent pas (et même qu'il existe une infinité de mots qui sont vraiment différents, c'est-à-dire qu'on ne peut pas passer de l'un à l'autre).
Précisons le théorème. Comme il s'agit de probabilités, on va devoir
prendre des grands nombres. Prenons donc des règles de longueur 100 (100
est le nombre de lettres à gauche du =, plus le nombre de lettres à
droite du = dans la règle). Commençons par nous demander combien il y a
de règles possibles de longueur 100 avec les lettres a, b, 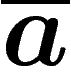 et
et
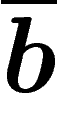 (explication rapide :
(explication rapide :  ). Le théorème dit qu'alors, le nombre limite
de règles à prendre est égal à
). Le théorème dit qu'alors, le nombre limite
de règles à prendre est égal à 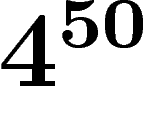 (c'est la racine de
(c'est la racine de 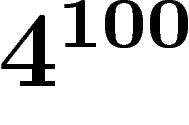 ). Autrement
dit :
). Autrement
dit :
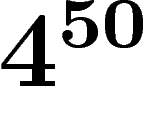 , alors je vous dis que vous allez très probablement pouvoir prouver que n'importe quel mot s'annule
, alors je vous dis que vous allez très probablement pouvoir prouver que n'importe quel mot s'annule
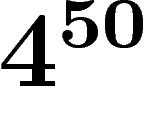 , alors je vous garantis que très
probablement votre jeu de mots sera intéressant, c'est-à-dire qu'il y aura des mots qui ne s'annulent pas, et il y en aura même une infinité de différents
, alors je vous garantis que très
probablement votre jeu de mots sera intéressant, c'est-à-dire qu'il y aura des mots qui ne s'annulent pas, et il y en aura même une infinité de différents
Commentaire : 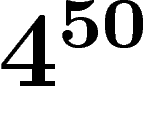 c'est grand, donc ce théorème garantit que si on se
donne des règles en nombre raisonnable, on aura (avec grande probabilité) des groupes intéressants !
c'est grand, donc ce théorème garantit que si on se
donne des règles en nombre raisonnable, on aura (avec grande probabilité) des groupes intéressants !
La réponse à la question de départ est : oui, on peut donc se donner des règles de calcul différentes de celles qu'on apprend à l'école, et ça ne donne pas n'importe quoi !