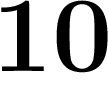 .
.
On veut voir ce qui se passe quand on change un peu les règles du calcul usuel. Lorsqu'on passe des nombres entiers aux nombres réels, on s'autorise à utiliser des nombres avec une infinité de chiffres après la virgule. Que se passerait-il si on essayait de calculer avec une infinité de chiffres avant la virgule ?
Ce n'est pas simplement un jeu gratuit : on obtient ainsi une théorie algébrique complète, dite p-adique, qui a certaines propriétés un peu plus simples que l'algèbre avec les nombres ordinaires. Elle est souvent étudiée par les mathématiciens, soit pour elle-même, soit pour tester des théorèmes qu'on veut démontrer pour les nombres ordinaires en se « faisant la main » sur le cas p-adique.
Les propriétés des nombres avec une infinité de chiffres à gauche vont
différer selon la base dans laquelle on travaille, comme on va le
montrer. On commence donc dans la base habituelle : la base 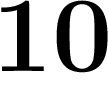 .
.
Un nombre décadique est donc un nombre avec une infinité de chiffres à
gauche, tel que 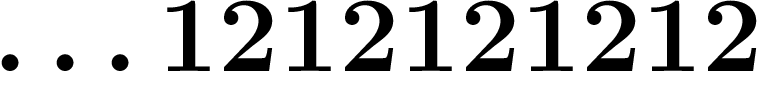 . On peut additionner les nombres
décadiques :
. On peut additionner les nombres
décadiques :
![\[
\begin{array}{r r}
& \ldots 12121212
\\ + & \ldots 95325368
\\ \hline
&\ldots 07446570
\end{array}
\]](padiques003.png)
Ceci fonctionne bien grâce à la propriété suivante : les n derniers
chiffres du nombre 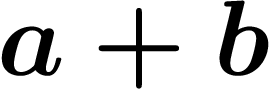 ne dépendent que des n derniers chiffres de
a et de b.
ne dépendent que des n derniers chiffres de
a et de b.
Par contre, on ne peut pas tout mélanger, i.e. avoir à la fois des nombres décadiques avec une infinité de chiffres à gauche, et des nombres réels ordinaires avec une infinité de chiffres à droite.
Il peut parfois se produire des propriétés amusantes lorsqu'on additionne des nombres décadiques :
![\[
\begin{array}{r r}
& \ldots 99999997
\\ + & 3
\\ \hline
&\ldots 00000000
\end{array}
\]](padiques005.png)
On a envie de dire qu'on a triché : la retenue est partie à l'infini vers
la gauche, mais elle existe ! Eh bien non : tout le truc des décadiques
consiste justement à dire que 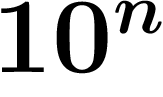 quand n est grand, c'est presque
rien : on ne voit que les derniers chiffres, les chiffres trop à gauche
ne comptent presque pas.
quand n est grand, c'est presque
rien : on ne voit que les derniers chiffres, les chiffres trop à gauche
ne comptent presque pas.
L'addition ci-dessus n'est absolument pas une contradiction : elle montre simplement qu'en décadiques, on a l'égalité
![\[
\ldots 99999997=-3
\]](padiques007.png)
On va montrer que grâce aux décadiques, on peut complètement se passer des signes ! Les nombres éngatifs sont déjà tout prêts.
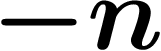 en p-adiques.
en p-adiques.
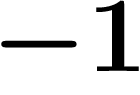 , on sait calculer
, on sait calculer 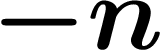 pour
n'importe quel nombre n, même si n est un décadique et non un nombre
ordinaire.
pour
n'importe quel nombre n, même si n est un décadique et non un nombre
ordinaire.
On a donc réussi à faire en décadiques trois des quatre opérations usuelles : addition, multiplication, soustraction.
Il y a des exemples de divisions qui marchent bien en décadiques. Par
exemple, pour calculer 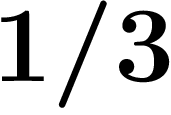 , il suffit de remarquer que
, il suffit de remarquer que
![\[
\begin{array}{r r}
& \ldots 66666667
\\ \times & 3
\\ \hline
&\ldots 00000001
\end{array}
\]](padiques012.png)
Cet exemple est une autre preuve qu'il ne faut pas
mélanger nombres décadiques et nombres réels : sinon, on aurait 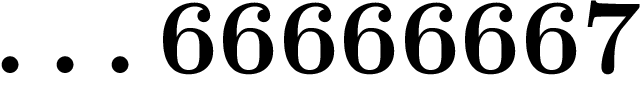 et
et 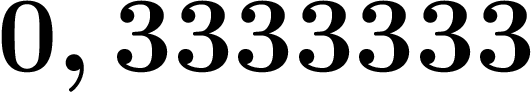 qui vaudraient tous les deux
qui vaudraient tous les deux 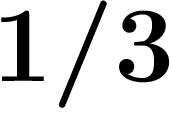 ...
...
Va-t-on, comme pour la soustraction, pouvoir se passer complètement des fractions et nombres à virgules en décadiques ? Pas tout à fait, parce qu'il y a quand même des problèmes. Regardons la tentative de division en décadiques :
![\[
\begin{array}{r r}
& \ldots ????????
\\ \times & 5
\\ \hline
&\ldots 00000001
\end{array}
\]](padiques016.png)
Pour commencer à résoudre cette division, il faut trouver un nombre a
entre 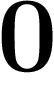 et
et  tel que a fois
tel que a fois  se termine par un
se termine par un 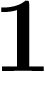 ... or ceci
n'existe pas.
... or ceci
n'existe pas.
Donc il n'est pas possible de faire n'importe quelle division en décadiques.
On peut remarquer ci-dessus que l'écriture de 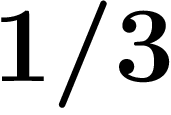 en décadiques évoque
fortement celle de
en décadiques évoque
fortement celle de 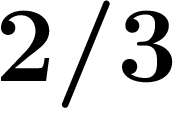 en nombres réels. Ça marche aussi pour d'autres
nombres :
en nombres réels. Ça marche aussi pour d'autres
nombres :
![\[
\begin{array}{r r}
& \ldots 142857142857143
\\ \times & 7
\\ \hline
&\ldots 000000000000001
\end{array}
\]](padiques023.png)
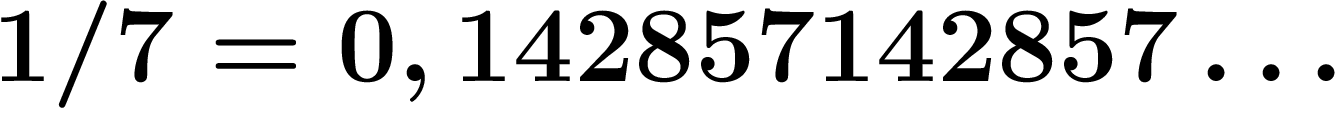
Pour cette question, il sera utile de remarquer qu'en nombres ordinaires,
des nombres tels que 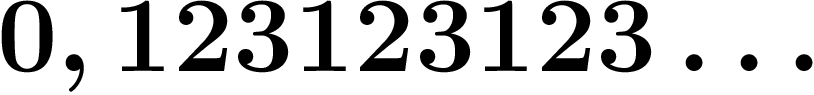 s'écrivent en fraction
s'écrivent en fraction
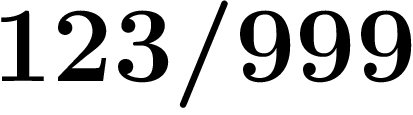 , et qu'en décadiques l'inverse d'un nombre tel que
, et qu'en décadiques l'inverse d'un nombre tel que 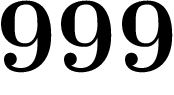 est
est
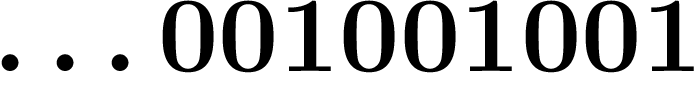 (faites la multiplication !).
(faites la multiplication !).
À ce stade, on a totalement étudié le problème du calcul des inverses des nombres entiers ordinaires. Savoir calculer des inverses suffit à faire des divisions, en remarquant que
![\[
a/b= a\times (1/b)
\]](padiques029.png)
Pour faire une opération en décadiques, il est absolument indispensable que les derniers chiffres du résultat de l'opération ne dépendent que des derniers chiffres des nombres de départ. (Repensez à l'exemple de la multiplication d'un décadique par un nombre décimal ordinaire à une infinité de chiffres à droite de la virgule.)
L'idée est donc que seuls les chiffres les plus à droite comptent, qu'on
voit moins les autres. En d'autres termes : 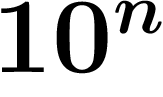 pour n grand, ça
tend vers
pour n grand, ça
tend vers 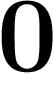 . C'est bien ce qu'on avait vu dans l'addition
. C'est bien ce qu'on avait vu dans l'addition
 .
.
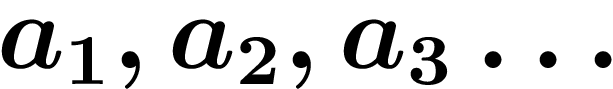 des nombres décadiques. On dit que cette suite
de décadiques tend vers une limite b si, lorsqu'on attend assez
longtemps, les derniers chiffres de tous les
des nombres décadiques. On dit que cette suite
de décadiques tend vers une limite b si, lorsqu'on attend assez
longtemps, les derniers chiffres de tous les 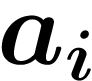 sont les mêmes que les
derniers chiffres de b.
sont les mêmes que les
derniers chiffres de b.
Par exemple, une suite qui commence par 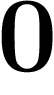 ;
;  ;
; 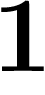 ;
; 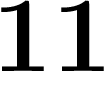 ;
; 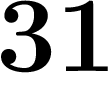 ;
;
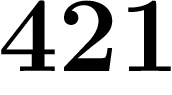 ;
; 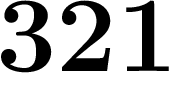 ;
; 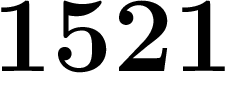 ;
; 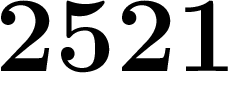 ;
; 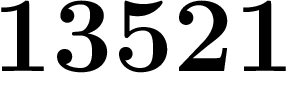 ;
; 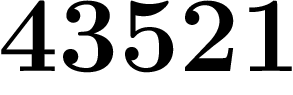 ;
; 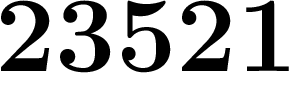 a l'air de se stabiliser vers un
nombre se finissant par
a l'air de se stabiliser vers un
nombre se finissant par 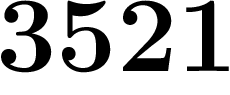 , puisqu'à partir du dixième terme, ces
quatre chiffres ne changent plus.
, puisqu'à partir du dixième terme, ces
quatre chiffres ne changent plus.
Donnons une définition plus formelle, qu'il est utile de comprendre :
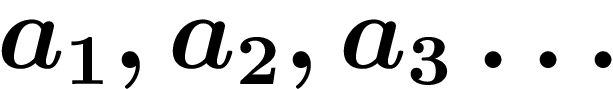 une suite de nombres décadiques. On dit que
cette suite tend vers une limite b si, pour tout nombre de chiffres n
qu'on se donne, il existe un i tel que, pour tout
une suite de nombres décadiques. On dit que
cette suite tend vers une limite b si, pour tout nombre de chiffres n
qu'on se donne, il existe un i tel que, pour tout 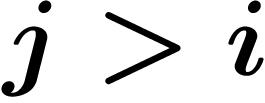 , les n derniers
chiffres de
, les n derniers
chiffres de 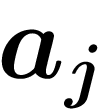 sont les mêmes que les n derniers chiffres de b.
sont les mêmes que les n derniers chiffres de b.
Par exemple, s'il y a une limite, on sait qu'à partir d'un certain
moment, les 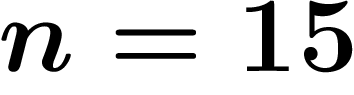 derniers chiffres ne vont plus bouger. Mais ce moment
peut être très éloigné, par exemple, il se peut qu'il faille attendre le
dix millième terme,
derniers chiffres ne vont plus bouger. Mais ce moment
peut être très éloigné, par exemple, il se peut qu'il faille attendre le
dix millième terme, 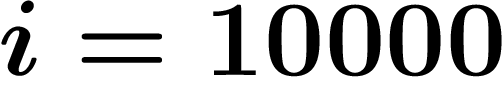 , avant que les n derniers chiffres ne
changent plus.
, avant que les n derniers chiffres ne
changent plus.
À quoi ça sert de définir ça ?
Jusqu'ici, nous n'avions réussi à diviser un décadique que par un nombre ordinaire. Nous n'avions pas tenté des expériences plus osées de division d'un décadique par un autre décadique...
On a bien envie de dire que pour diviser par un décadique, il suffit de
diviser par les n derniers chiffres, puis de prendre la limite quand
n tend vers l'infini. Autrement dit, on aimerait que pour diviser par
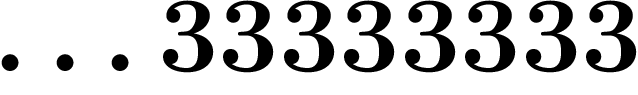 , il suffise de diviser par
, il suffise de diviser par  , par
, par  , par
, par 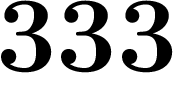 ,
etc. et de voir si on obtient une limite comme ça.
,
etc. et de voir si on obtient une limite comme ça.
On veut donc montrer très exactement la propriété suivante : que si la
suite d'entiers 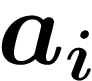 tend vers un décadique b, alors la suite de
décadiques
tend vers un décadique b, alors la suite de
décadiques 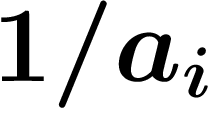 tend vers l'entier
tend vers l'entier 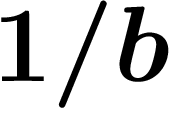 . (Attention, on a vu
ci-dessus que tous les entiers n'avaient pas d'inverse, par exemple,
si'ils se terminaient par
. (Attention, on a vu
ci-dessus que tous les entiers n'avaient pas d'inverse, par exemple,
si'ils se terminaient par  ; on suppose donc qu'on n'est pas dans ce
cas et que les
; on suppose donc qu'on n'est pas dans ce
cas et que les 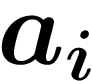 ont bien des inverses.)
ont bien des inverses.)
Qu'est-ce qui se passe quand on essaie de changer le dénominateur d'une fraction par une quantité petite ? Ceux qui savent sommer des séries géométriques connaissent sûrement la formule :
![\[
\frac{1}{1+x}=1-x+x^2-x^3+x^4-\ldots
\]](padiques062.png)
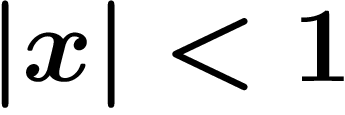 , autrement dit si
, autrement dit si
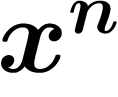 tend vers
tend vers  quand n est grand.
quand n est grand.
Si vous ne connaissez pas cette formule, multipliez le terme de droite
par le dénominateur de gauche  et remarquez que tous les termes se
téléscopent et qu'il reste
et remarquez que tous les termes se
téléscopent et qu'il reste  .
.
Cette formule se généralise si on a autre chose que 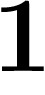 au dénominateur :
au dénominateur :
![\[
\frac1{c+x}=\frac1c \frac1{1+x/c} = \frac1c \left(
1-(x/c)+(x/c)^2-(x/c)^3+\ldots\right)
\]](padiques069.png)
En décadiques, c'est 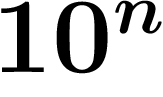 qui tend vers
qui tend vers 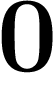 quand n est grand...
Imaginons donc que nous avons un décadique a dont le dernier chiffre
est
quand n est grand...
Imaginons donc que nous avons un décadique a dont le dernier chiffre
est 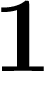 . On veut calculer
. On veut calculer 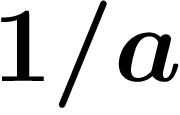 . On
remarque que
. On
remarque que 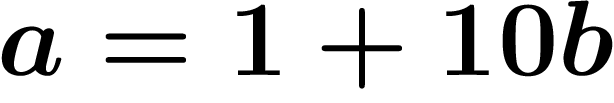 où b est un décadique : c'est exactement dire
que le dernier chiffre de a est
où b est un décadique : c'est exactement dire
que le dernier chiffre de a est 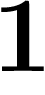 .
.
Mais alors on a envie de dire que, comme ci-dessus,
![\[
\frac1a=\frac1{1+10b}=1-10b+(10b)^2-(10b)^3+(10b)^4-\ldots
\]](padiques076.png)
Si le dernier chiffre n'est pas un 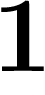 , on applique le même truc que
ci-dessus, à savoir que
, on applique le même truc que
ci-dessus, à savoir que
![\[
\frac1{c+10b}=\frac1c \frac1{1+10(b/c)}
\]](padiques078.png)
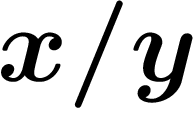 .
.
Bien sûr, si l'on donne une suite de décadiques, elle n'a pas toujours de
limite. Par exemple, 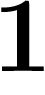 ;
;  ;
; 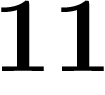 ;
; 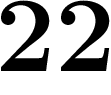 ;
; 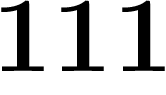 ;
; 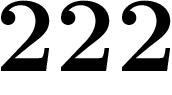 , etc., ne
tend vers rien du tout. On a quand même envie de dire, plutôt qu'elle
n'a pas de limite, qu'elle en aurait deux. C'est l'intérêt de la notion
de limite extraite.
, etc., ne
tend vers rien du tout. On a quand même envie de dire, plutôt qu'elle
n'a pas de limite, qu'elle en aurait deux. C'est l'intérêt de la notion
de limite extraite.
Si 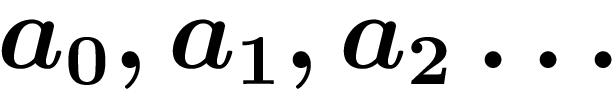 est une suite, on appelle sous-suite extraite de
la suite
est une suite, on appelle sous-suite extraite de
la suite 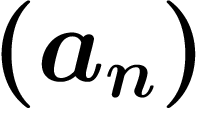 une suite
une suite 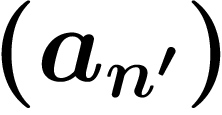 incluse dans celle-là, c'est-à-dire
qu'on ne prend pas tous les termes (mais qu'on en prend quand même une
infinité). Par exemple, on peut prendre un terme sur deux, ou bien
prendre seulement les termes
incluse dans celle-là, c'est-à-dire
qu'on ne prend pas tous les termes (mais qu'on en prend quand même une
infinité). Par exemple, on peut prendre un terme sur deux, ou bien
prendre seulement les termes 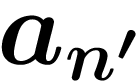 où
où 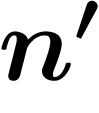 est un carré, etc.
est un carré, etc.
Ainsi, dans l'exemple de la suite  ;
;  ;
; 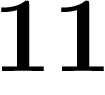 ;
; 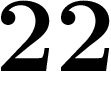 ;
; 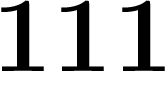 ;
;
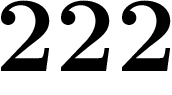 , on a envie de la séparer en deux sous-suites en prenant un terme sur
deux, et chacune aura une limite.
, on a envie de la séparer en deux sous-suites en prenant un terme sur
deux, et chacune aura une limite.
La suite ci-dessus a donc deux limites extraites 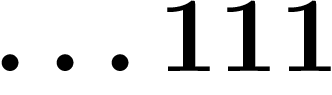 et
et
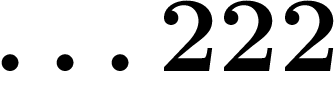 .
.
Si l'on sait bien que toutes les suites n'ont pas de limites, on aimerait bien avoir quand même des limites extraites...
La compacité est une notion extrêmement importante en mathématiques, qui
est utilisée dans tous les domaines. Par exemple, on peut montrer que
l'intervalle ![$[0;1]$](padiques099.png) est compact (pour la limite d'une suite de nombres
réels). On peut aussi montrer que toute partie du plan qui ne va pas
jusqu'à l'infini est compacte (pour la limite de points du plan).
est compact (pour la limite d'une suite de nombres
réels). On peut aussi montrer que toute partie du plan qui ne va pas
jusqu'à l'infini est compacte (pour la limite de points du plan).
Par contre, l'ensemble des entiers ordinaires n'est pas compact : la bête
suite 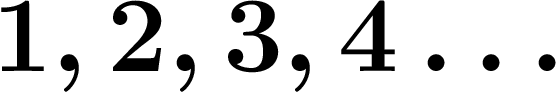 ne tend vers rien du tout.
ne tend vers rien du tout.
Mais en y ajoutant les décadiques, il devient compact. Par exemple, de la
suite des entiers 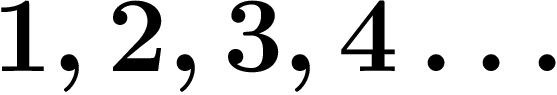 on peut extraire la sous-suite
on peut extraire la sous-suite 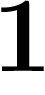 ,
,
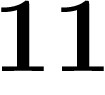 ,
, 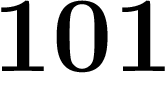 ,
, 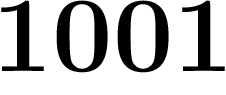 ,
, 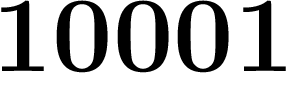 ,
, 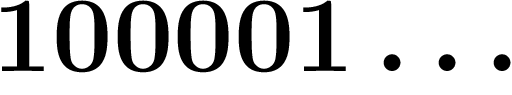 , qui dans les décadiques a
pour limite
, qui dans les décadiques a
pour limite 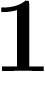 ! (Le
! (Le 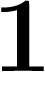 de devant part à l'infini et disparaît...)
de devant part à l'infini et disparaît...)
C'est joli, mais à quoi ça sert ?
Vous avez sans doute déjà remarqué que, si on prend deux nombres a et
b se terminant par  et
et  , leur produit se terminera par un
, leur produit se terminera par un 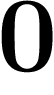 . En
fouillant un peu, on peut trouver des nombres de trois chiffres dont le
produit se termine par trois zéros (par exemple,
. En
fouillant un peu, on peut trouver des nombres de trois chiffres dont le
produit se termine par trois zéros (par exemple, 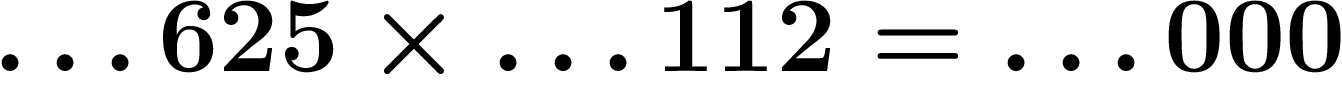 ), etc.
), etc.
Dans les nombres ordinaires, il n'y a pas de diviseurs de 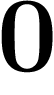 .
.
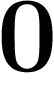 ?
?
(Indice : remarquer que 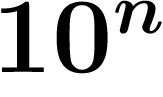 tend vers
tend vers 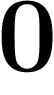 , que
, que  et
utiliser la compacité.)
et
utiliser la compacité.)
On a vu ci-dessus qu'il était impossible en général de diviser en décadiques par
certains nombres, par exemple par  ou par
ou par  .
.
Et pourtant, tout le monde sait que  et
et 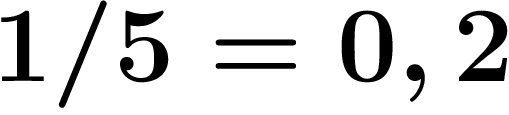 ... on aurait
bien envie de les rajouter.
... on aurait
bien envie de les rajouter.
Faisons-le.
(On est obligé de se limiter à un nombre fini de chiffres à droite, sinon
on a déjà vu qu'on aura des problèmes pour définir la multiplication, et
qu'en plus on risque de se retrouver avec deux nombres différents égaux à
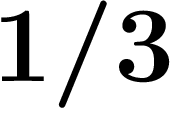 ...)
...)
Maintenant, on a le droit de diviser par  ou par
ou par  .
.
(Penser qu'un nombre se décompose en facteurs premiers.)
Attention : pas tous !
On rappelle qu'un anneau est un ensemble sur lequel on a les opérations ordinaire d'addition, de soustraction et de multiplication, avec les règles habituelles (mais pas forcément la division).
Si donc vous avez répondu « tous » à la question précédente et que vous
avez construit des diviseurs de 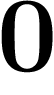 auparavant, vous avez dit des
bêtises.
auparavant, vous avez dit des
bêtises.
Pour inverser  et
et  , on avait simplement rajouté
, on avait simplement rajouté 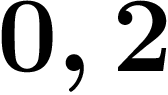 et
et 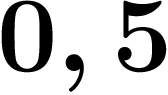 .
Mais la question précédente montre qu'on ne peut pas faire pareil pour
les diviseurs de zéro : quelle que soit la manière dont on essaie
de rajouter des nouveaux nombres, on n'arrivera jamais à leur trouver des
inverses (à moins de tomber sur une contradiction).
.
Mais la question précédente montre qu'on ne peut pas faire pareil pour
les diviseurs de zéro : quelle que soit la manière dont on essaie
de rajouter des nouveaux nombres, on n'arrivera jamais à leur trouver des
inverses (à moins de tomber sur une contradiction).
On a travaillé en base 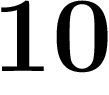 , et on a remarqué tout le long que
, et on a remarqué tout le long que  et
et  nous emmmbêtaient.
nous emmmbêtaient.
On peut essayer d'écrire les nombres en base p (c'est-à-dire qu'un
nombre tel que 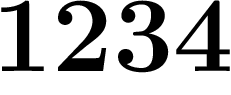 signifiera
signifiera 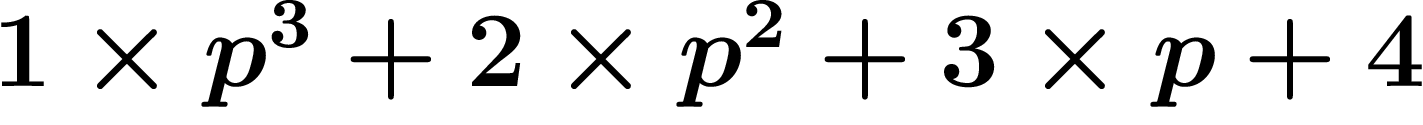 au
lieu de
au
lieu de 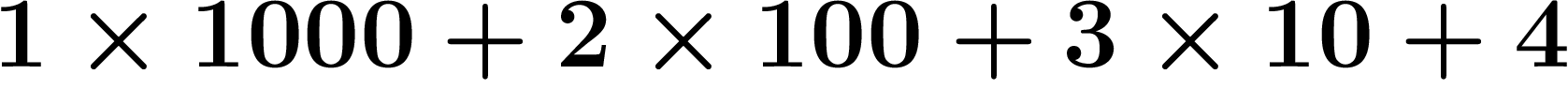 ).
).
Cela fera peut-être disparaître le problème des  et des
et des  ...
...
Les entiers p-adiques sont notés 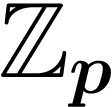 . Les p-adiques à virgule sont
notés
. Les p-adiques à virgule sont
notés 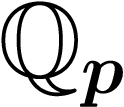 .
.
Vérifier la multiplication suivante en base 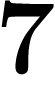 :
:
![\[
\begin{array}{r r}
& \ldots 254125413_7
\\ \times & 5_7
\\ \hline
&\ldots 000000001_7
\end{array}
\]](padiques142.png)
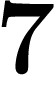 , l'inverse de
, l'inverse de  est
est 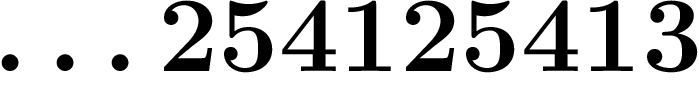 . Maintenant,
. Maintenant,
 a donc un inverse.
a donc un inverse.
On peut reprendre toutes les questions précédentes. Ce qui est très important est que les réponses ne sont pas les mêmes en fonction de p : cela veut dire que les nombres qu'on obtient en autorisant une infinité de chiffres à gauche dépendent de la base dans laquelle on écrit !
On a donc des anneaux.
Remarquer qu'en base p, l'inverse de p s'écrit simplement 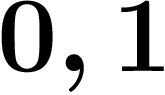 dans les
p-adiques à virgule : de même que
dans les
p-adiques à virgule : de même que 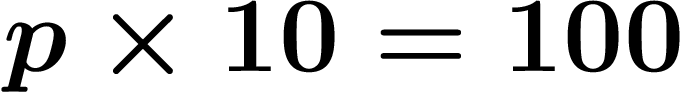 en base p, on a
en base p, on a
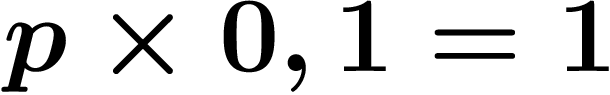 , autrement dit
, autrement dit 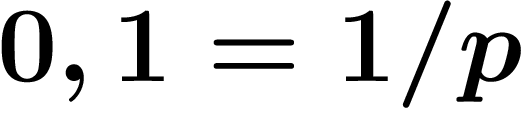 .
.
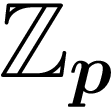 ? Et dans
? Et dans
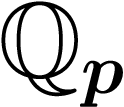 ?
?
Là encore, il est utile de remarquer que pour savoir diviser par tous les nombres ordinaires, il suffit de savoir diviser par tous les nombres premiers !
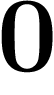 ?
?
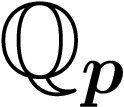 ne sont pas tous les mêmes pour tous les p.
ne sont pas tous les mêmes pour tous les p.
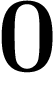 ) ont des
inverses, on dit qu'on a un corps.
) ont des
inverses, on dit qu'on a un corps.
Remarquer que les p-adiques sans virgule ne sont pas un corps, parce
que p lui-même n'y est jamais inversible (son inverse, c'est toujours
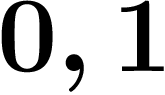 ).
).
L'étude des corps en général est l'un des domaines les plus importants des mathématiques. Il existe des centaines de théorèmes sur le sujet, et on en découvre de nouveaux chaque année.
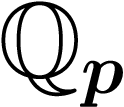 est-il un corps ?
est-il un corps ?
Souvent, l'ensemble 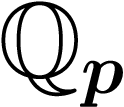 est plus facile à traiter que l'ensemble
est plus facile à traiter que l'ensemble 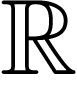 des nombres réels. C'est pourquoi, souvent, on essaie de résoudre des
problèmes (par exemple des équations) dans
des nombres réels. C'est pourquoi, souvent, on essaie de résoudre des
problèmes (par exemple des équations) dans 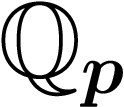 et, s'il y a des
solutions dans
et, s'il y a des
solutions dans 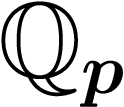 , on essaie de les transférer dans
, on essaie de les transférer dans 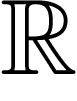 .
.