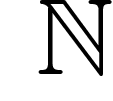 dans un ensemble A appelé alphabet. On prendra ici
dans un ensemble A appelé alphabet. On prendra ici  . Un mot fini
de longueur n est une application de
. Un mot fini
de longueur n est une application de  dans A (ou le mot vide si
dans A (ou le mot vide si 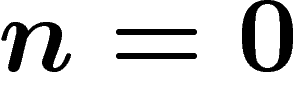 ).
).
On étudie ici des mots infinis constitués de a et de b, et qui possèdent la propriété d'être de complexité minimale parmi les mots non périodiques : les mots sturmiens.
On étudiera certaines de leurs propriétés combinatoires, puis on recherchera un procédé itératif systématique pour les engendrer. Ce faisant, outre la définition de départ, on aura trouvé deux autres définitions équivalentes de ces mots.
On s'intéressera aussi à des ensembles de mots sturmiens appelés systèmes dynamiques sturmiens, définis à partir de l'itération d'un opérateur, et qui lient des mots sturmiens partageant certaines propriétés.
Un mot infini est une application de 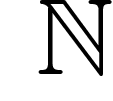 dans un ensemble A appelé alphabet. On prendra ici
dans un ensemble A appelé alphabet. On prendra ici  . Un mot fini
de longueur n est une application de
. Un mot fini
de longueur n est une application de  dans A (ou le mot vide si
dans A (ou le mot vide si 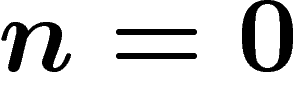 ).
).
Un facteur d'un mot u est un mot fini constitué de lettres consécutives de u.
Le langage d'un mot u est l'ensemble de ses facteurs.
La complexité d'un mot u est l'application qui à chaque 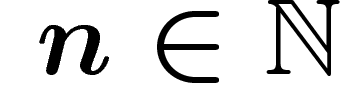 associe le nombre de facteurs de u de longueur n
différents. On notera
associe le nombre de facteurs de u de longueur n
différents. On notera 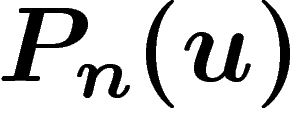 ce nombre.
ce nombre.
Un mot infini u est dit sturmien si 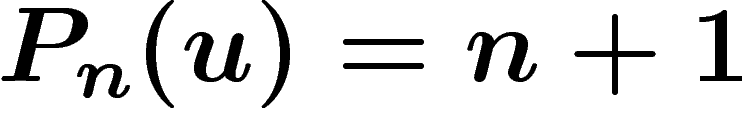 , ou encore s'il contient exactement
, ou encore s'il contient exactement 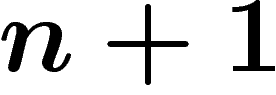 facteurs différents de
longueur n.
facteurs différents de
longueur n.
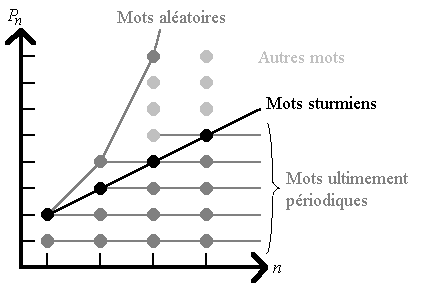
Le choix de la valeur 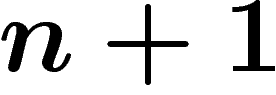 peut sembler arbitraire. En fait, comme annoncé en
introduction, les mots sturmiens sont les mots de complexité minimum
(l'ensemble des complexités étant ordonné par l'ordre lexicographique) parmi
les mots non périodiques. On peut en effet montrer que s'il existe
peut sembler arbitraire. En fait, comme annoncé en
introduction, les mots sturmiens sont les mots de complexité minimum
(l'ensemble des complexités étant ordonné par l'ordre lexicographique) parmi
les mots non périodiques. On peut en effet montrer que s'il existe 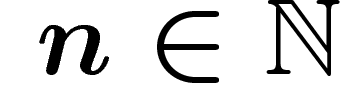 tel que
tel que 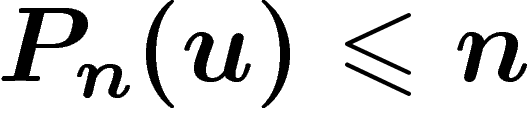 ,
alors u est périodique (à partir d'un certain rang), et réciproquement. La
complexité
,
alors u est périodique (à partir d'un certain rang), et réciproquement. La
complexité 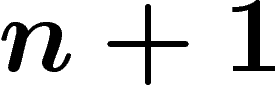 est donc un minimum pour les mots non périodiques :
est donc un minimum pour les mots non périodiques :
La complexité 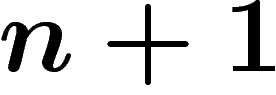 signifie aussi que lorsqu'on considère les facteurs d'un mot de longueur n, il existe exactement
un facteur U tel que Ua et Ub soient facteurs de ce mot, tous les autres facteurs de longueur n étant prolongeables
à droite d'une unique manière.
signifie aussi que lorsqu'on considère les facteurs d'un mot de longueur n, il existe exactement
un facteur U tel que Ua et Ub soient facteurs de ce mot, tous les autres facteurs de longueur n étant prolongeables
à droite d'une unique manière.
Un mot infini u est dit équilibré si le nombre de a dans deux de ses facteurs de même longueur diffère de 0 ou 1.
On obtient une définition équivalente en remplaçant a par b.
Il se trouve qu'on a quasi-identité entre les mots sturmiens et les mots équilibrés.
Un mot non périodique est sturmien si et seulement s'il est équilibré.
Un mot équilibré est donc soit périodique (à partir d'un certain rang), soit sturmien, et, comme un mot sturmien n'est jamais périodique, tout mot sturmien est équilibré.
On a donc obtenu jusqu'ici une double définition des mots sturmiens. On va maintenant définir trois processus dynamiques de génération de mots, qui fourniront une troisième caractérisation des mots sturmiens.
Un premier exemple est constitué des mots de billard. On considère la trajectoire d'une boule ponctuelle soumise aux lois de réflexion de Descartes dans un billard :
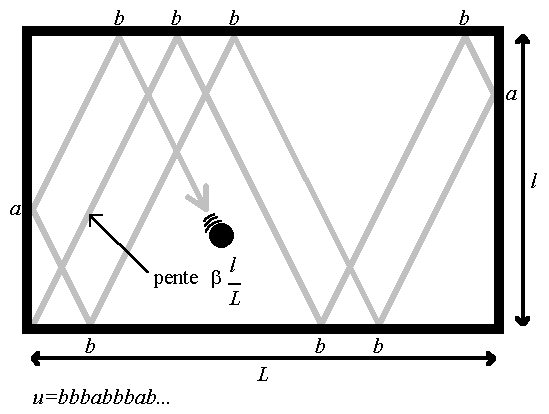
En l'absence de pertes d'énergie, la boule rencontre les parois un nombre
infini de fois. On repère par un a un choc avec une paroi verticale, et par
un b un choc avec une paroi horizontale. On obtient ainsi un mot infini. Ce
mot est noté 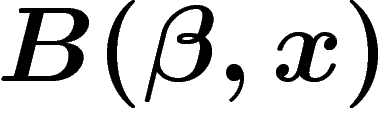 où
où 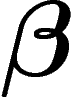 et x sont la pente et l'ordonnée à
l'origine de la droite que constitue la trajectoire de la boule avant le
premier choc. On prendra
et x sont la pente et l'ordonnée à
l'origine de la droite que constitue la trajectoire de la boule avant le
premier choc. On prendra 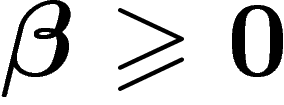 . La pente est calculée relativement aux longueurs des
côtés du billard (la diagonale du billard ayant une pente 1).
. La pente est calculée relativement aux longueurs des
côtés du billard (la diagonale du billard ayant une pente 1).
Les mots de billard vérifient la propriété suivante :
Il est périodique si et seulement si 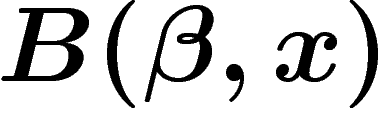 est équilibré.
est équilibré.
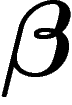 est rationnel.
est rationnel.
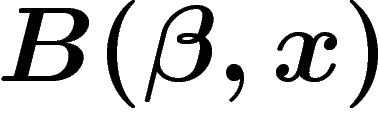 est donc sturmien si et seulement si
est donc sturmien si et seulement si 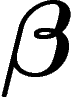 est
irrationnel.
est
irrationnel.
Les mots de billard sont liés à un autre ensemble de mots dont l'interprétation est de nature géométrique, les mots de Christoffel. Ils répondent au problème de l'approximation d'une droite par des points à coordonnées entières (qui se pose par exemple lors du tracé de droites sur un écran d'ordinateur). On considère une droite passant par l'origine, de pente comprise entre 0 et 1, et on l'approche par une suite de points dont les abscisses sont les entiers successifs, et les ordonnées, les plus grands entiers tels que le point reste sous la droite :
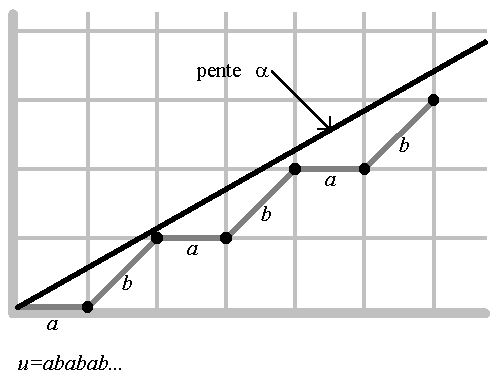
On construit ensuite un mot infini : lorsque deux points successifs ont même
ordonnée, on écrit un a, et un b lorsque l'ordonnée varie. On obtient ainsi le
mot de Christoffel associé à une droite de pente  . On peut généraliser la
construction au cas où la droite a une ordonnée à l'origine x non nulle (qu'on
prendra entre 0 et 1, par invariance du mot associé par addition d'un entier).
Le mot correspondant sera noté
. On peut généraliser la
construction au cas où la droite a une ordonnée à l'origine x non nulle (qu'on
prendra entre 0 et 1, par invariance du mot associé par addition d'un entier).
Le mot correspondant sera noté 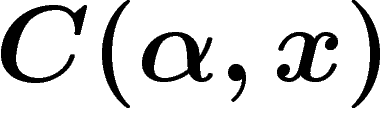 .
.
Il existe une bijection entre mots de billard et mots de Christoffel :
![\[
B(\beta,x)=C\left(\frac{\beta}{\beta+1},\frac{\beta+x}{\beta+1}\right)
\]](sturm023.png)
On vérifie que les intervalles de pente et d'ordonnée à l'origine pour lesquels ces mots sont définis entraînent bien le caractère bijectif.
Conséquence immédiate :
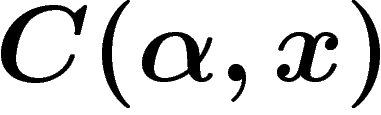 est équilibré. Il est sturmien si et seulement si
est équilibré. Il est sturmien si et seulement si  est irrationnel, périodique sinon.
est irrationnel, périodique sinon.
On peut donner une construction alternative des mots de Christoffel :
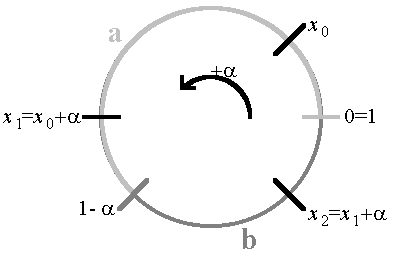
On se donne un nombre 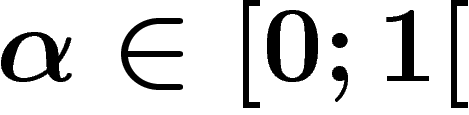 et on considère l'opération qui consiste à ajouter
et on considère l'opération qui consiste à ajouter  modulo 1. On construit ainsi, à
partir d'un nombre
modulo 1. On construit ainsi, à
partir d'un nombre 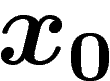 , une suite
, une suite  de nombres de
de nombres de 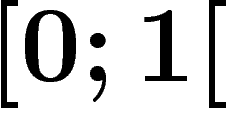 . Cette suite est interprétée comme un mot en
écrivant un a si
. Cette suite est interprétée comme un mot en
écrivant un a si 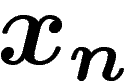 est inférieur à
est inférieur à  , et un b sinon. Cette construction redonne
, et un b sinon. Cette construction redonne 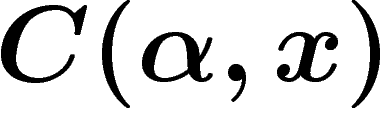 . On dira que ce mot est
engendré par la rotation d'angle
. On dira que ce mot est
engendré par la rotation d'angle  .
.
Un point reste flou dans les trois constructions ci-dessus : le comportement à
adopter lorsque la boule du billard heurte un coin, lorsque la droite de
Christoffel passe par un point à coordonnées entières, et lorsque l'un des
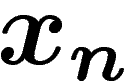 vaut 0 ou
vaut 0 ou  . Deux conventions cohérentes sont possibles. Elles ne
donnent des résultats différents que dans un nombre dénombrable de cas. Par la
suite, on dira qu'un mot est engendré par une rotation s'il l'est avec l'une ou
l'autre des conventions.
. Deux conventions cohérentes sont possibles. Elles ne
donnent des résultats différents que dans un nombre dénombrable de cas. Par la
suite, on dira qu'un mot est engendré par une rotation s'il l'est avec l'une ou
l'autre des conventions.
On savait déjà que les mots engendrés par des rotations d'angle irrationnel étaient sturmiens. La réciproque est vraie :
Un mot est sturmien si et seulement s'il est engendré par une rotation irrationnelle.
On peut remarquer que l'existence des deux conventions ci-dessus n'est pas fortuite : la définition combinatoire des mots sturmiens s'interprète en remarquant que parmi tous les facteurs d'un mot sturmien, un exactement est prolongeable à gauche par a et par b (une propriété du même type sera vraie pour les systèmes sturmiens, cf. ci-dessous) : ce cas correspond précisément au cas où la droite de Christoffel passe par un point à coordonnées entières (ou encore au cas où la boule arrive dans un coin du billard).
On s'intéresse dorénavant à des ensembles de mots définis par l'itération d'un opérateur (d'où le qualificatif " dynamique "), en liaison avec des propriétés topologiques. On verra que ces systèmes sont en rapport avec la construction des mots sturmiens par les rotations irrationnelles.
On définit une topologie sur l'ensemble des mots infinis, induite par la distance ultramétrique
![\[
d(u,v)=2^{-\inf \{n\in \N,u_n\neq v_n\}}
\]](sturm037.png)
L'ensemble des mots infinis est compact pour cette topologie.
L'ensemble des mots sturmiens est d'intérieur vide, de mesure nulle. Son adhérence est l'ensemble des mots équilibrés.
L'application qui à chaque mot sturmien associe l'angle de la rotation qui l'engendre est continue.
On définit sur l'ensemble des mots l'opérateur " décalage " (pour Shift) qui consiste à retirer la première lettre :

C'est un opérateur lipschitzien d'ordre 2.
Il possède les trois propriétés des opérateurs usuellement appelés chaotiques : la densité des points périodiques, la propriété de brassage et la dépendance sensitive aux conditions initiales.
Le système dynamique associé au mot sturmien u est l'adhérence de son orbite sous l'opérateur S.
C'est un fermé d'intérieur vide, stable par S.
Tous les mots d'un système sturmien jouent des rôles équivalents :
Le système associé à un mot sturmien est l'ensemble des mots ayant le même langage.
Tout mot d'un système sturmien est sturmien et engendre le système.
Il existe une autre caractérisation des systèmes sturmiens, qui fournit une bijection (même un homéomorphisme avec une bonne topologie) entre les systèmes sturmiens et les irrationnels de :
Deux mots sturmiens appartiennent au même système si et seulement s'ils sont engendrés par des rotations de même
angle.
Dans chaque système sturmien, il existe un unique mot biprolongeable à gauche (i.e. au et bu appartiennent
au système). Ce mot est 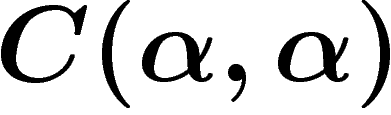 où
où  est l'angle de la rotation associée.
est l'angle de la rotation associée.
On retrouve ici la propriété typique des facteurs d'un mot sturmien, à l'échelle d'un système.
Soit 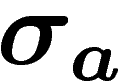 (resp.
(resp. 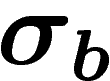 ) le morphisme de monoïde (pour la
concaténation) qui à a associe a (resp. ab) et à b, ba (resp. b).
) le morphisme de monoïde (pour la
concaténation) qui à a associe a (resp. ab) et à b, ba (resp. b).
Soit un système sturmien associé à l'irrationnel  et dont le mot biprolongeable est v.
et dont le mot biprolongeable est v.
On écrit la décomposition de  en fraction continue :
en fraction continue :
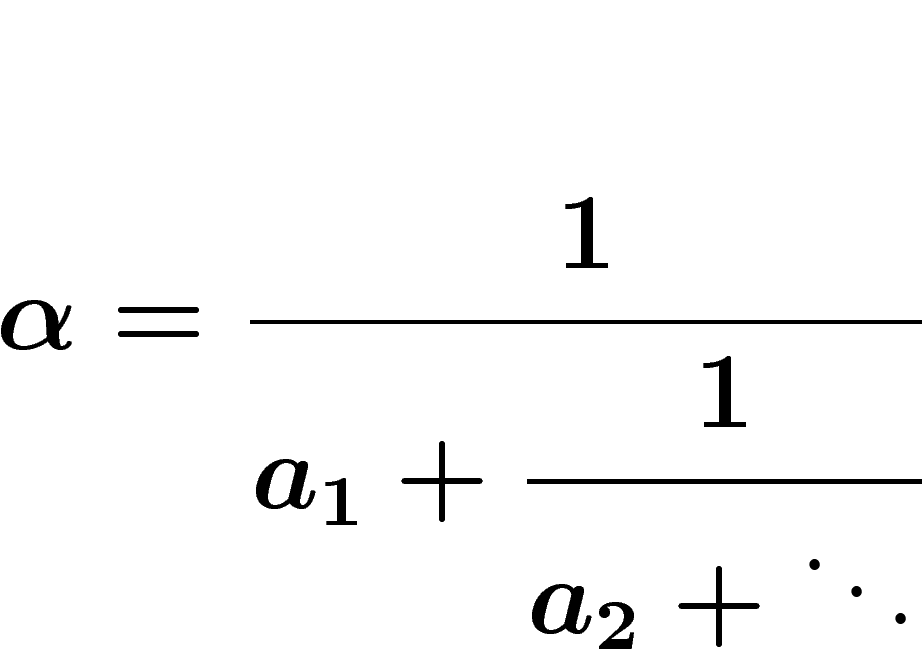
Alors
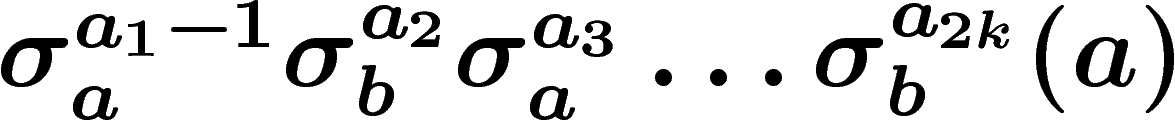 et
et
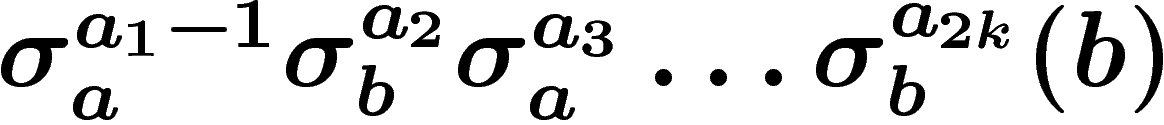 sont des préfixes de abv et bav respectivement.
sont des préfixes de abv et bav respectivement.
Ce résultat qui peut sembler abscons donne en fait des informations
précises sur la structure du mot. Par exemple, le mot correspondant sera
composé de 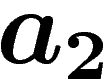 ou
ou 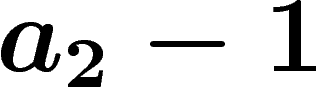 séquences successives
séquences successives 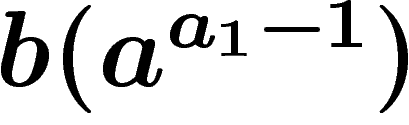 entrecoupées de séquences
entrecoupées de séquences 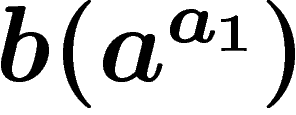 , etc.
, etc.
Cette relation fournit de plus un algorithme rapide (en 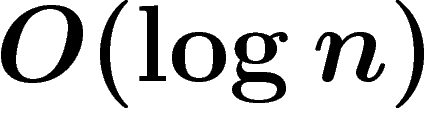 ) pour calculer des approximations d'un mot sturmien
ainsi que pour retrouver l'angle à partir du mot.
) pour calculer des approximations d'un mot sturmien
ainsi que pour retrouver l'angle à partir du mot.
On construit par récurrence une suite de mots en partant des deux mots
a et ab et en concaténant à chaque étape les deux mots précédents, de
manière analogue à la construction de la suite de Fibonacci
(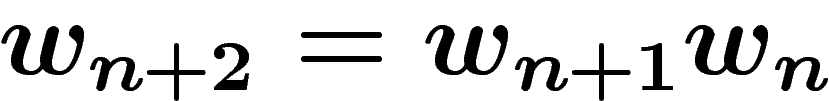 ). La suite ainsi définie converge vers le mot de
Fibonacci.
). La suite ainsi définie converge vers le mot de
Fibonacci.
C'est aussi le point fixe de l'application contractante sur l'ensemble des mots (finis et infinis) qui consiste à remplacer les a par des ab et les b par des a.
C'est, enfin, et de manière surprenante, le mot biprolongeable du système
sturmien associé à 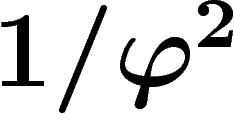 où
où  est le nombre
d'or.
est le nombre
d'or.
On a obtenu une triple caractérisation des mots sturmiens (complexité, équilibre, rotations)
On a aussi une triple caractérisation des systèmes sturmiens (opérateur S, langage, angle de la rotation).
Sujet de l'agrégation de mathématiques 1994, option Mathématiques de l'informatique.
C. Bourguignat, T. Fajour et R. Zara, Complexité de suites. Suites sturmiennes, in Quadrature 26 (1996).