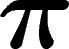 décimale par
décimale, et montre comment ce type d'algorithme peut se généraliser au
calcul d'autres irrationnels, comme e ou
décimale par
décimale, et montre comment ce type d'algorithme peut se généraliser au
calcul d'autres irrationnels, comme e ou 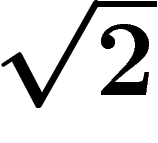 .
.
Cet article traite d'un algorithme de calcul de 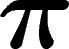 décimale par
décimale, et montre comment ce type d'algorithme peut se généraliser au
calcul d'autres irrationnels, comme e ou
décimale par
décimale, et montre comment ce type d'algorithme peut se généraliser au
calcul d'autres irrationnels, comme e ou 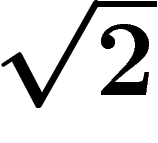 .
.
Tout commence avec un mystérieux programme trouvé sur une messagerie électronique (cf.
L'accélération de la convergence, Jean-Paul Delahaye, Pour la Science 199, mai 1994) qui
calcule 2400 décimales de 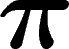 quatre par quatre à une vitesse plutôt impressionnante.
quatre par quatre à une vitesse plutôt impressionnante.
Le voici en langage C :
long a=10000,b=0,c=8400,d,e=0,f[8401],g;
main(){for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4ld",e+d/a),e=d%a)
for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);}
Le même en Pascal :
var
a,b,c,d,e,g:longint;
f:array[0..8400]of longint;
procedure affiche(i:integer);
begin
if i>999 then write(i) else
if i>99 then write('0',i) else
if i>9 then write('00',i) else write('000',i);
end;
begin
a:=10000;b:=0;c:=4200;e:=0;
for b:=0 to c do f[b]:=a div 5;
while(c>0)do begin
d:=0;g:=c*2;b:=c;
while(b>0) do begin
d:=d+f[b]*a;dec(g);f[b]:=d mod g;
d:=d div g;dec(g);dec(b);
if(b>0)then d:=d*b;
end;
dec(c,14);
affiche(e+d div a);
e:=d mod a;
end;
readln;
end.
(reconnaissons que le C est d'une admirable concision)
Ce programme est original par le fait qu'il calcule non pas un nombre ou une suite convergeant
vers 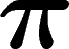 (style
(style 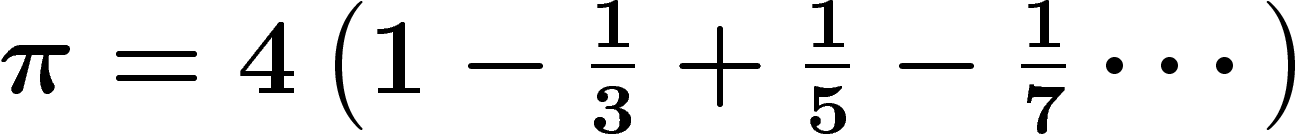 ,
pour donner la plus connue et la plus lente), mais des blocs de décimales
(plus ou moins) indépendamment les uns des autres (cf. Les algorithmes
compte-gouttes, Ian Stewart, Pour la Science 215, septembre 1995).
,
pour donner la plus connue et la plus lente), mais des blocs de décimales
(plus ou moins) indépendamment les uns des autres (cf. Les algorithmes
compte-gouttes, Ian Stewart, Pour la Science 215, septembre 1995).
Ceci fait penser aux méthodes de conversion d'un nombre écrit dans une base donnée vers son écriture dans une autre base.
Observons le petit calcul suivant, qui est un début de conversion
en base 10 du nombre 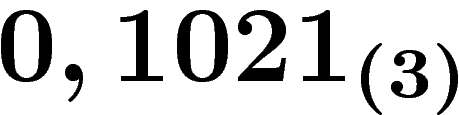 .
.
La méthode utilisée consiste à introduire un facteur 10 en dernière position, que l'on fait ensuite "remonter" par des divisions euclidiennes, de manière à obtenir le début d'un développement décimal accompagné d'un "reste" en base 3 :
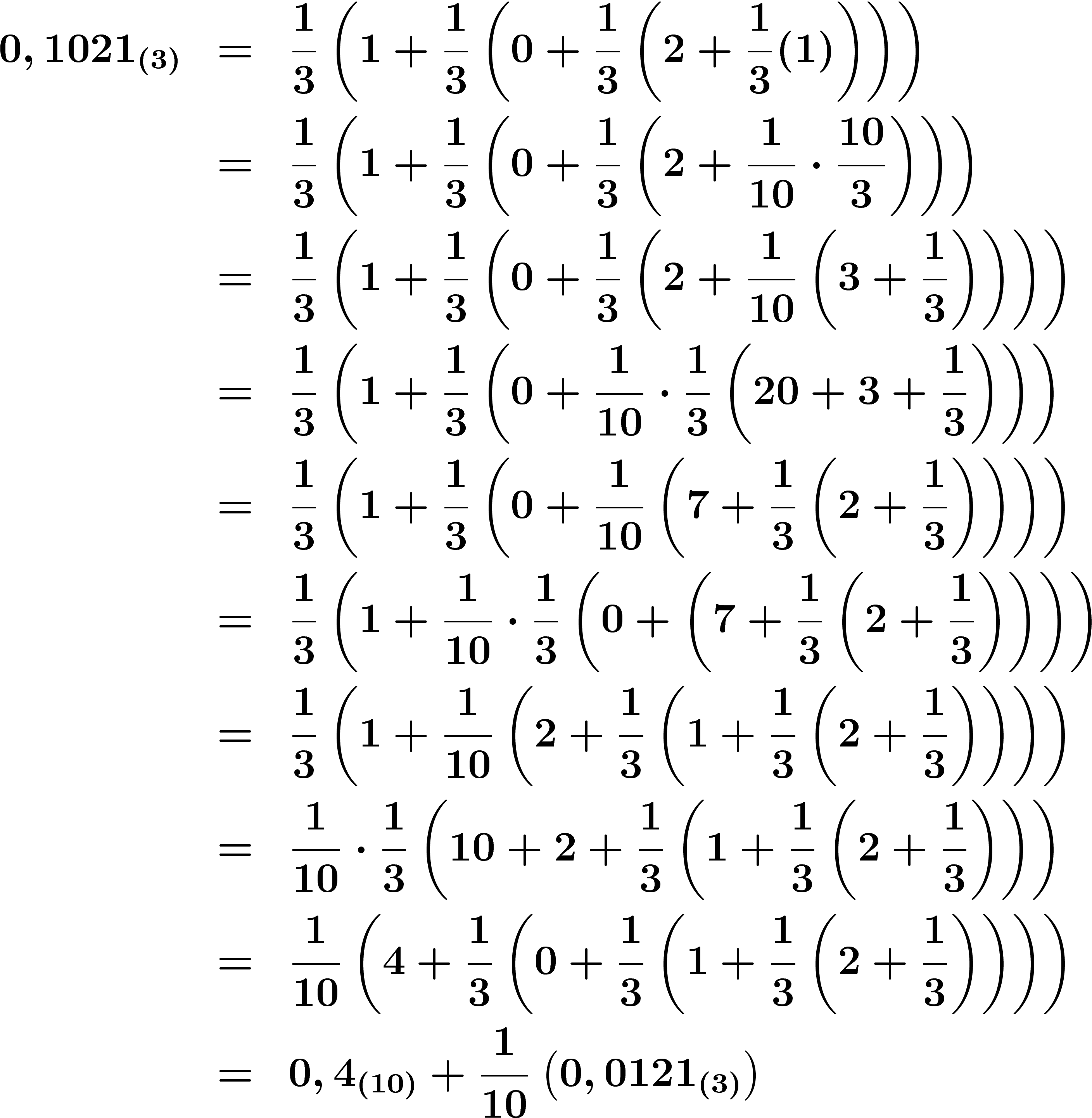
Pour achever la conversion, il ne restera plus ensuite qu'à appliquer la même méthode au "reste" donné par l'algorithme.
J'invite le lecteur à écrire un petit programme effectuant la première étape de la conversion en utilisant cette méthode, à comparer ensuite à la version ci-dessous (en C puis en Pascal).
long a=10,//base destination
b,c=4,//nombre de chiffres
d=0,f[5],g=3;//base source
main()
{f[0]=0;f[1]=1;f[2]=0;f[3]=2;f[4]=1;//nombre à convertir
for(b=c;d+=f[b]*a,f[b]=d%g,d/=g,--b;);
printf("%ld",d);}
var
a,b,c,d,g:longint;
f:array[0..8400]of longint;
begin
a:=10;{base destination}
c:=4;{nombre de chiffres}
g:=3;{base source}
f[0]:=0;f[1]:=1;f[2]:=0;f[3]:=2;f[4]:=1;{nombre à convertir}
d:=0;
for b:=c downto 1 do begin
d:=d+f[b]*a;f[b]:=d mod g;
d:=d div g;
end;
writeln(d);
readln;
end.
L'affichage produit est "4" et le tableau f[] contient ensuite le "reste" (0,0,1,2,1) de l'algorithme. Pour continuer la conversion, il suffit de faire boucler le programme en réutilisant le "reste", en remettant d à 0 et en affichant les résultats les uns à la suite des autres.
Ce programme présente une certaine ressemblance avec la boucle intérieure de celui présenté en début d'article ("Comme c'est étrange et quelle coïncidence!" dirait Ionesco).
On peut cependant remarquer une différence notable : dans le cas du
calcul de 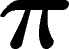 , la variable g
change au cours de l'exécution. Ceci est dû au fait qu'une extension de la notion de base est
possible : on peut considérer, étant donnée une suite
, la variable g
change au cours de l'exécution. Ceci est dû au fait qu'une extension de la notion de base est
possible : on peut considérer, étant donnée une suite
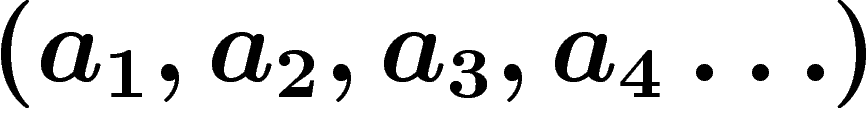 de rationnels, qu'un nombre qui
s'écrit
de rationnels, qu'un nombre qui
s'écrit
![\[
b=a_1(b_1+a_2(b_2+a_3(b_3+a_4(b_4+\cdots ))))
\]](pi011.png)
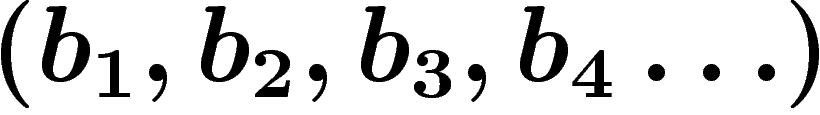 dans la base
dans la base
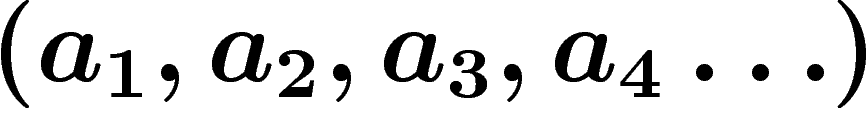 .
.
Notre vieille base 10 est alors la base
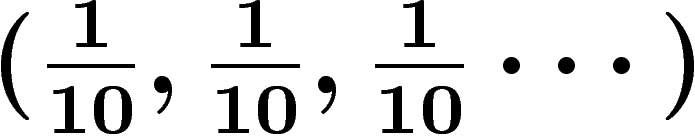
À noter que, si l'on n'impose pas de condition supplémentaire, on n'a pas unicité de l'écriture d'un nombre.
Ici intervient la formule
![\[
\pi=2+\frac13\left(2+\frac25\left(2+\frac37\left(2+\frac49\left(2+\cdots\right)\right)\right)\right)
\]](pi015.png)
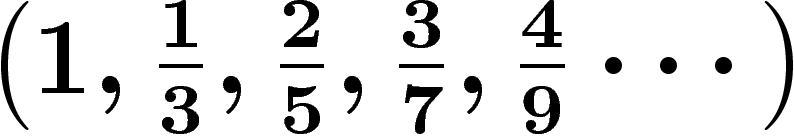 ,
, 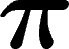 s'écrit
s'écrit
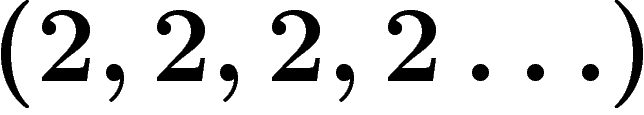 .
.
Le programme qui nous occupe n'est donc qu'un algorithme de conversion de cette base en base 10. La variable g contrôle le dénominateur des fractions, et b est à la fois le numéro de la décimale et le numérateur des fractions, ce qui explique leurs décrémentations respectives.
En fait, ce programme calcule non pas en base 10 mais en base 10000, ce
qui explique l'affichage quatre par quatre des décimales. De plus, pour
gagner trois décimales, on calcule 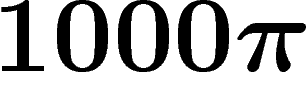 au lieu de
au lieu de 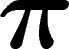 (d'où l'affectation
de a/5 au lieu de 2 à f[], ce qui est correct quand a est une puissance
de 10). La conversion est cependant plus délicate qu'auparavant. En
effet, on doit faire des "divisions euclidiennes" par un rationnel, i.e.
on écrit par exemple
(d'où l'affectation
de a/5 au lieu de 2 à f[], ce qui est correct quand a est une puissance
de 10). La conversion est cependant plus délicate qu'auparavant. En
effet, on doit faire des "divisions euclidiennes" par un rationnel, i.e.
on écrit par exemple 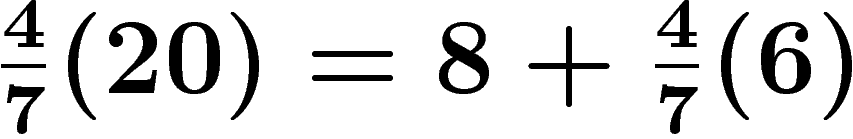 . Dans cette opération, on doit d'abord effectuer
une division euclidienne par le dénominateur ( d/=g ou d:=d div
g), dont
le résultat est ensuite remultiplié par le numérateur ( d*=b ou {tt
d:=d*b}).
Ceci peut avoir des conséquences gênantes dans la mesure où le reste est
composé de nombres inférieurs seulement aux dénominateurs de chaque
fraction, ce qui fait que la "décimale" calculée à l'étape suivante avec
ce reste peut allègrement dépasser 10. Ceci oblige à avoir une décimale
d'avance sur l'affichage, afin de reporter les excès sur la décimale
précédente. C'est le rôle de la variable "tampon" e. Il est même parfois
insuffisant d'avoir un seul chiffre d'avance, phénomène d'autant plus
marqué que la base destination est petite. En tout cas, des erreurs
subsistent toujours, par exemple quand on rencontre plusieurs 9 (en base
10) de suite, cas où une modification entraîne la nécessité de révisions
en cascade.
. Dans cette opération, on doit d'abord effectuer
une division euclidienne par le dénominateur ( d/=g ou d:=d div
g), dont
le résultat est ensuite remultiplié par le numérateur ( d*=b ou {tt
d:=d*b}).
Ceci peut avoir des conséquences gênantes dans la mesure où le reste est
composé de nombres inférieurs seulement aux dénominateurs de chaque
fraction, ce qui fait que la "décimale" calculée à l'étape suivante avec
ce reste peut allègrement dépasser 10. Ceci oblige à avoir une décimale
d'avance sur l'affichage, afin de reporter les excès sur la décimale
précédente. C'est le rôle de la variable "tampon" e. Il est même parfois
insuffisant d'avoir un seul chiffre d'avance, phénomène d'autant plus
marqué que la base destination est petite. En tout cas, des erreurs
subsistent toujours, par exemple quand on rencontre plusieurs 9 (en base
10) de suite, cas où une modification entraîne la nécessité de révisions
en cascade.
Dernier problème : 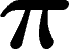 a un développement illimité. On doit donc majorer le nombre de décimales
à utiliser. Un calcul rapide montre que pour obtenir p décimales, pour
p grand, il suffit que le nombre
n de chiffres de
a un développement illimité. On doit donc majorer le nombre de décimales
à utiliser. Un calcul rapide montre que pour obtenir p décimales, pour
p grand, il suffit que le nombre
n de chiffres de 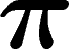 à utiliser vérifie
à utiliser vérifie 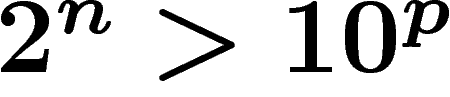 , soit
, soit
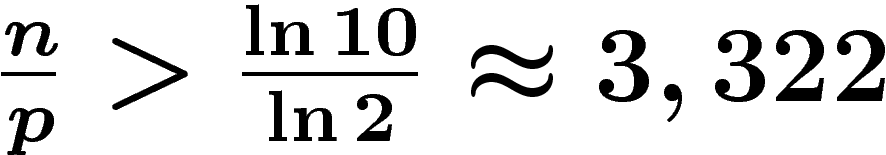 . En base 10000, cela donne
. En base 10000, cela donne
 , ce qui explique le fait que le programme affiche 600=8400/14 blocs de 4
décimales, ainsi que le décrément de 14 subi par la variable c.
, ce qui explique le fait que le programme affiche 600=8400/14 blocs de 4
décimales, ainsi que le décrément de 14 subi par la variable c.
À ce stade, le programme initial est totalement expliqué.
Au vu de tout ceci, il est très facile de généraliser : en modifiant la variable a, on peut calculer dans une base quelconque. Il faut bien sûr réévaluer le nombre minimal de chiffres à utiliser et, lorsque la base est trop petite, utiliser plusieurs variables-tampon.
Autre généralisation possible : utiliser le même principe pour calculer d'autres nombres remarquables. Les développements en série des fonctions usuelles fournissent des expressions qui se prêtent souvent bien au traitement dans une base simple.
Le plus bel exemple est sans doute le
nombre e, qui s'écrit 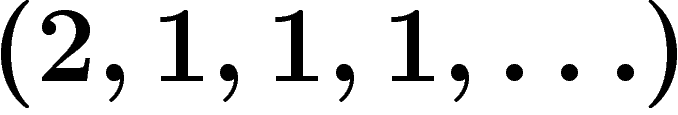 dans la base
dans la base
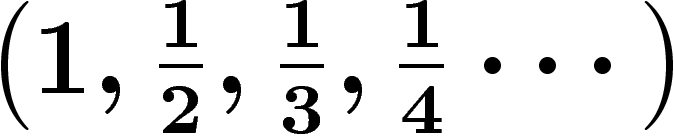 ; de plus cet exemple est très
avantageux quant au nombre de chiffres à utiliser.
; de plus cet exemple est très
avantageux quant au nombre de chiffres à utiliser.
Dans la même veine, on peut citer les fonctions de trigonométrie
hyperbolique. Autre possibilité : dans la base
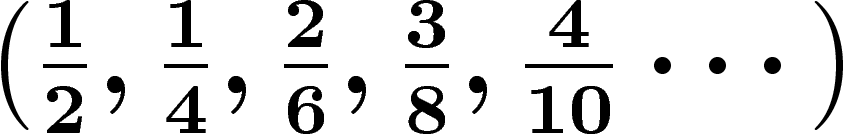 ,
, 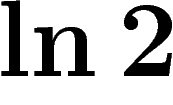 s'écrit
s'écrit 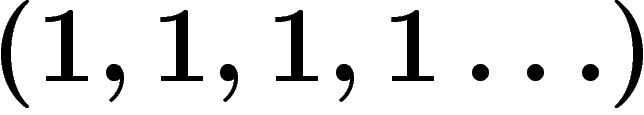 . Etc.
. Etc.
Il est aussi possible mais fastidieux de traiter des expressions comportant des changements de
signe : certaines "décimales" obtenues sont négatives, et il est donc nécessaire de les réinterpréter, le
résultat n'étant pas particulièrement lisible au premier coup d'oeil
(ainsi 0 2 -1 signifie 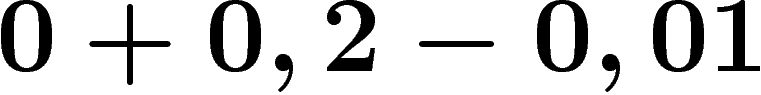 soit 0,19). On peut par exemple
utiliser l'expression classique (de Machin)
soit 0,19). On peut par exemple
utiliser l'expression classique (de Machin)
![\[
\pi= 16\arctan \frac15 - 4\arctan \frac1{239}
\]](pi033.png)
L'intérêt de cette méthode ne se limite pas aux fonctions transcendantes.
Ainsi on peut calculer 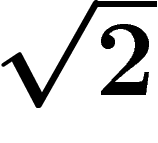 en utilisant le développement de
en utilisant le développement de
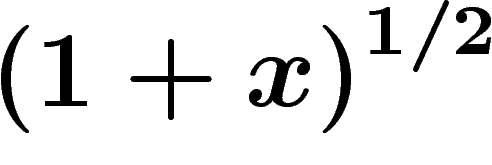 ; mais le coût en nombre de chiffres est dans ce cas très
lourd, et il est plus intéressant, dans le même but, de calculer
; mais le coût en nombre de chiffres est dans ce cas très
lourd, et il est plus intéressant, dans le même but, de calculer
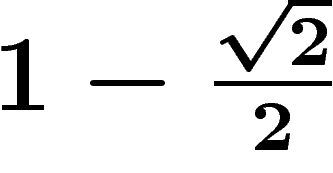 qui s'écrit
qui s'écrit 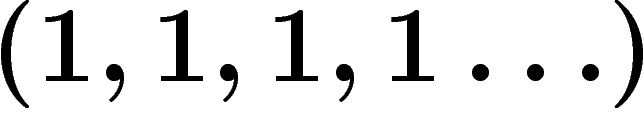 dans la
base
dans la
base
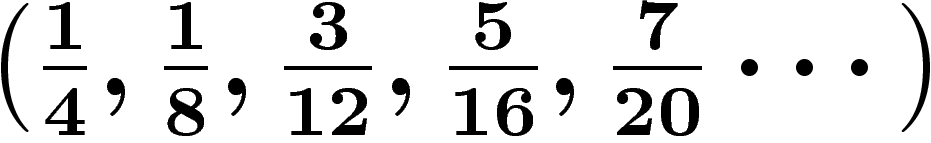 .
.
Cette méthode est donc très générale et a l'avantage de n'utiliser que des nombres entiers, sans arithmétique en virgule flottante. Elle a le défaut de nécessiter un temps de calcul croissant généralement comme le carré du nombre de décimales à obtenir, ce qui n'est quand même pas trop mal.