peut se transformer en 
car les longueurs
des côtés sont conservées (il est entendu que ces transformations se font uniquement dans le plan).
Un treillis est alors un "grillage" composé de tels losanges. Par exemple : 
.
Le titre parle de flexibilité et non de rigidité car, quand on est sur un échafaudage, les conséquences de sa flexibilité sont plus graves que celles de sa rigidité.
Un treillis de barres articulées a pour élément fondamental un losange dont les coins sont
flexibles mais les côtés de longueur fixe. Ainsi peut se transformer en car les longueurs
des côtés sont conservées (il est entendu que ces transformations se font uniquement dans le plan).
Un treillis est alors un "grillage" composé de tels losanges. Par exemple : .
Par contre, les losanges ne peuvent pas "se plier" selon une de leurs diagonales. Si ABCD est un losange, on interdit donc à C de venir se placer en A, car ce changement nécessiterait une rotation dans l'espace autour de (BD), alors que ces transformations se font uniquement dans le plan.
D'autre part, un carré du treillis peut être rendu rigide par l'adjonction d'une barre diagonale.
Ainsi 
devient 
. Il est évident que la barre diagonale choisie n'influence pas le reste du
treillis (puisqu'on a interdit aux points diagonalement opposés de se confondre). Un carré rigide sera
donc représenté par un carré plein.
Exemple :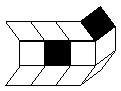 
.
Par manque de place, je ne donnerai pas ici de définition plus rigoureuse de ce qu'est un treillis.
désignera l'ensemble des couples de lignes et de colonnes contenant un carré rigide.
Les losanges d'un treillis seront souvent appelés "carrés", par abus de langage.
On appellera direction d'une ligne (resp. colonne) la direction verticale (resp. horizontale) de ses losanges. Cette direction est toujours la même puisque les côtés opposés d'un losange sont parallèles. On dira que la direction d'une ligne (resp. colonne) est celle d'un carré si elle est la direction verticale (resp. horizontale) de ce carré.
Deux treillis seront dits superposables si l'on peut passer de l'un à l'autre par isométrie directe, sans tenir compte des carrés rigides. Deux treillis seront dits égaux si l'on passe de l'un à l'autre par isométrie directe, en tenant compte de la disposition des carrés rigides.
Un treillis sera dit déformable s'il existe un treillis différent ayant même taille et même disposition des carrés rigides. Le treillis ci-dessus est évidemment déformable, par exemple en :
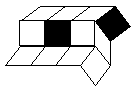
Deux treillis t et t' sont dits semblables si et seulement si l'un peut se déformer en l'autre ou s'ils
sont égaux, autrement dit s'ils ont même taille et 
.
Par la suite, on désignera souvent indifféremment par treillis une classe d'équivalence de treillis selon l'égalité ou la similitude. La phrase "le treillis t peut..." signifiera souvent "il existe un treillis semblable à t tel que...".
Deux treillis t et t' sont dits équivalents si et seulement si pour tout treillis t2 semblable à t, il
existe un treillis t'2 semblable à t' tel que t2 et t'2 soient superposables. Cela signifie que ces deux
treillis ont les mêmes manières de se déformer. Deux treillis peuvent être équivalents sans que les
carrés rigides soient disposés de la même façon. Par exemple,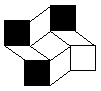 
équivaut à 
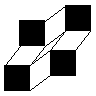car ils se déforment exactement des mêmes façons.
La "superposabilité", l'égalité, la similitude, l'équivalence des treillis sont des relations d'équivalence.
Un treillis t est dit rigide si et seulement si tout treillis semblable lui est égal, ou plus simplement s'il ne peut pas se déformer.
On dit d'un carré 
d'un treillis t qu'il ne peut pas se déformer (ou
qu'il est indéformable) si et seulement si les points correspondants dans un quelconque treillis
semblable à t forment un carré. Cela ne signifie pas que ce carré est rigide! Ainsi les carrés rigides
où 
ne peuvent pas se déformer, mais la réciproque
n'est pas vraie. Ainsi des treillis semblables ont les mêmes carrés indéformables.
Le graphe associé à un treillis est défini comme suit.
On prend l'exemple du treillis 
.
1) On représente les lignes et colonnes du treillis par des points disposés de la manière suivante : 
.
2) Pour chaque carré rigide (x;y), on trace un segment entre le point représentant la x-ième
colonne et la y-ième ligne :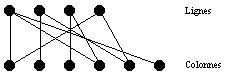 
.
Un graphe caractérise une classe de treillis semblables.
Une question intéressante (elle est même fondamentale) est de savoir si un treillis donné,
comportant des carrés rigidifiés et non rigidifiés, est rigide. Ainsi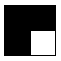 
est rigide : le carré en bas
à droite ne peut se déformer sans entraîner une déformation des autres, ce qui est impossible. Mais
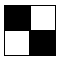n'est pas rigide. Il peut se déformer, par exemple, en 
.
Théorème
(i) Si deux lignes (respectivement colonnes) d'un treillis appartiennent à la
même composante connexe du graphe associé, alors dans tout treillis
semblable leurs directions sont les mêmes, et réciproquement.
(ii) Si une ligne et une colonne d'un treillis appartiennent à la même
composante connexe, alors dans tout treillis semblable la direction de la
ligne est perpendiculaire à celle de la colonne, et réciproquement.
Tout d'abord, on est autorisé à parler de "direction" d'une ligne et d'une colonne car comme le treillis est composé de losange, tous les côtés verticaux (resp. horizontaux) des losanges d'une ligne (resp. colonne) ont la même direction. Considérons donc une ligne et une colonne reliées dans le graphe par une arête. Cela signifie qu'à leur intersection se trouve un carré rigide, et donc pour tout treillis de la classe représentée par le graphe, la ligne et la colonne auront des directions perpendiculaires. Ce résultat s'étend par récurrence sur le nombe d'arêtes à toutes les lignes et colonnes d'une même composante connexe.
La réciproque s'obtient en construisant un treillis semblable au treillis considéré, dans lequel deux lignes de composantes connexes différentes (resp. deux colonnes, une ligne et une colonne) n'ont pas des directions parallèles (resp. parallèles, perpendiculaires). Pour ce faire, on construit d'abord un treillis sans carré rigide en prenant garde à donner à toutes les lignes d'une future composante connexe du graphe la même direction, et à toutes les colonnes de cette composante connexe, une direction perpendiculaire. On peut alors choisir les directions à donner à chaque future composante connexe de telle sorte que les deux lignes (resp. ...) considérées aient des directions différentes, et même des directions quelconques l'une par rapport à l'autre. Il suffit ensuite de rigidifier les carrés désirés, ce qui est toujours possible : en effet, les carrés à rigidifier se trouvent par définition entre une ligne et une colonne de la même composante connexe du graphe, lesquelles ont grâce à cette construction soigneuse des directions perpendiculaires, ce qui autorise la rigidification. On vérifie facilement que le treillis ainsi construit est semblable au treillis de départ.
Utilité principale du graphe :
Corollaires
Un losange est indéformable si et seulement si sa ligne et sa colonne
appartiennent à une même composante connexe du graphe.
Le treillis représenté est rigide si et seulement si le graphe obtenu est connexe.
Pour tout losange d'un treillis, l'une des deux propositions suivantes est
vraie : soit dans tout treillis semblable au treillis considéré, ses directions
verticale et horizontale sont perpendiculaires (le sens de l'angle étant
toujours le même), soit étant donné un couple quelconque de directions, il
existe un treillis semblable dans lequel ce losange présente ces directions.
Le troisième corollaire, seul non trivial, résulte du fait que dans la démonstration de la réciproque du théorème, on peut fixer les directions des deux lignes considérées de manière indépendante.
Théorème
(i) Il est toujours possible de rigidifier un treillis de longueur L et de largeur
l en y plaçant convenablement L + l - 1 carrés rigides.
(ii) Il n'est jamais possible de le rigidifier en en plaçant moins.
En effet, il s'agit de relier de manière connexe tous les points du graphe. Le nombre de lignes
nécessaire et suffisant pour relier n points de manière connexe est trivialement 
, ce qui
démontre le théorème. Comme le graphe comporte L + l points, on doit y placer L + l - 1 lignes. Le
fait que certains points ne puissent être reliés à d'autres (car ils représentent tous deux une ligne ou
une colonne) n'intervient pas (il suffit de choisir un autre point déjà lié aux autres pour obtenir la
liaison).
Les lignes et colonnes correspondant à une composante connexe du graphe associé à un treillis forment une région du treillis. Ceci dans le sens qu'elles peuvent se déformer sans entraîner de déformation du reste du treillis.
Comme la réunion des éléments des composantes connexes du graphe forme le graphe lui-même, il s'ensuit que chaque ligne, chaque colonne et chaque losange du treillis appartiennent à une région (on dit qu'une ligne ou une colonne appartient à une région si le sommet du graphe qui la représente y appartient, et qu'un losange appartient à une région si sa ligne ou sa colonne y appartient). Un carré rigide, une ligne, une colonne n'appartiennent qu'à une région (un carré rigide correspond à une arête du graphe, une ligne et une colonne à un sommet). Remarque : un carré non rigide peut faire partie de plusieurs régions du treillis (penser à un treillis sans carré rigide), mais peut aussi n'appartenir qu'à une région (comme dans le cas d'un treillis rigide).
Un treillis rigide ne comporte qu'une région et réciproquement.
L'ensemble des carrés (rigides ou non) qui appartiennent à une même région et uniquement à cette région forme une zone rigide de la région, du treillis.
Tous les carrés rigides d'une région sont inclus dans la zone rigide de cette région. Ceci découle immédiatement de la définition et du fait qu'un carré rigide n'appartient qu'à une région. Chaque carré rigide appartient donc à une unique zone rigide.
Pourquoi zone "rigide"?
Les carrés d'une zone rigide sont indéformables. Inversement, chaque carré indéformable appartient à une et une seule zone rigide.
Démonstration : un carré appartient à une zone rigide si et seulement si sa ligne et sa colonne appartiennent à la même région, donc à la même composante connexe, et sont donc connectées dans le graphe. Leurs directions sont alors perpendiculaires, et ces carrés ne peuvent pas se déformer. Le raisonnement se fait à l'envers pour la réciproque.
Théorème
Deux treillis sont équivalents si et seulement s'ils ont les mêmes carrés
indéformables.
Démonstration : deux treillis équivalents ont évidemment les mêmes carrés indéformables. Si deux treillis ont les mêmes carrés indéformables, considérons un treillis t1 semblable au premier. Il existe un treillis t2 semblable au second qui lui est superposable. En effet les carrés indéformables de t2 ont même direction que ceux de t1, et de plus ses carrés déformables peuvent prendre des directions arbitraires (corollaires précédents), donc en particulier celles des carrés déformables de t1. Tous les carrés de ces deux treillis ont donc même direction, ce qui prouve qu'ils sont superposables. Les deux treillis de départ sont donc équivalents.
Corollaire
Les régions et zones rigides d'un treillis ne sont pas modifiées par passage à
un treillis équivalent. Inversement, si deux treillis ont les mêmes zones
rigides (ou régions) ils sont équivalents.
La donnée des zones rigides (ou des régions) caractérise donc de manière
unique l'ensemble des treillis équivalents à un treillis donné.
Ceci car les carrés indéformables de treillis équivalents sont les mêmes (théorème précédent), ce qui implique qu'une ligne et une colonne liées le sont toujours par passage à un treillis équivalent, ce qui équivaut à l'invariance des composantes connexes. Il en est donc de même pour les zones rigides.
On appellera treillis représentant d'une région non réduite à un sommet, le treillis formé en supprimant dans le treillis de départ toutes les lignes et colonnes non comprises dans la région. Ceci revient à ne considérer que la zone rigide de la région.
Tout treillis représentant d'une région non réduite à un sommet est rigide.
Tous les résultats concernant les treillis, en particulier les treillis rigides, peuvent s'appliquer aux zones rigides de régions non dégénérées. Il suffira de redéfinir les concepts appropriés : longueur, largeur, rigidité, R(t), etc., d'une zone rigide, comme étant ceux du treillis représentant.
Un carré rigide d'un treillis est dit redondant s'il existe un treillis équivalent dans lequel ce carré
n'est pas rigide. Par exemple, le carré (ligne 3, colonne 2) de 
est redondant : ce treillis
se déforme des mêmes manières que 
.
Un treillis est dit redondant s'il comporte au moins un carré redondant. Un treillis non redondant est dit simple.
Sur le graphe représentant le treillis, le trait représentant un carré redondant relie donc une ligne et une colonne qui seraient déjà reliées sans lui, donc le graphe forme une boucle. Ceci permet d'affirmer qu'un carré redondant n'existe jamais seul : en effet, on peut supprimer un quelconque autre trait de la boucle du graphe. Comme cette boucle est formée au minimum de quatre arêtes (puisque le graphe est biparti), les carrés redondants vont toujours au moins par quatre.
Si plusieurs carrés sont redondants, il se peut qu'on ne puisse pas les supprimer tous en même temps. Ceci se produit uniquement si ces carrés appartiennent à la même boucle. En réalité, le nombre de carrés rigides d'un graphe pouvant être supprimés n'est pas égal au nombre de carrés redondants, mais au nombre de boucles du graphe. On obtient ainsi dans le treillis des groupes de carrés redondants appartenant à la même boucle du graphe, dont un peut être supprimé dans chaque groupe, mais pas plusieurs. (On peut tirer de ceci des conclusions philosophiques sur l'utilité individuelle et collective...)
Voici en cascade quelques résultats simples si on les interprète en termes de graphes (on
rappelle aux lecteurs distraits que 
désigne l'ensemble des couples de lignes et de colonnes
contenant un carré rigide).
Si 
et t est simple, t est rigide.
Si 
et t est déformable, t est redondant.
Si t est simple et rigide, 
.
Si t est rigide et 
, t est simple.
Si 
, t est redondant.
Théorème
Si on rigidifie tous les carrés indéformables d'un treillis, l'ensemble des
treillis équivalents s'obtient en supprimant successivement un nombre
quelconque de carrés redondants. Autrement dit : on passe d'un treillis à un
treillis équivalent par adjonctions et retraits successifs de carrés redondants.
Réciproquement, si l'ajout ou la suppression d'un carré rigide ne modifie pas
les régions et zones rigides, le carré est redondant.
En effet, l'adjonction ou le retrait de carrés redondants ne modifie pas l'interdépendance de leur ligne et de leur colonne (puisqu'ils sont redondants), et donc les régions du treillis, ce qui prouve qu'on obtient des treillis équivalents. Le fait que tous les treillis équivalents puissent effectivement être atteints découle du fait que deux treillis équivalents ayant les mêmes carrés indéformables, si on rigidifie tous ces carrés indéformables, on obtient le même treillis à partir de deux treillis équivalents, ce qui prouve que partant de l'un on peut atteindre l'autre (le nombre minimal d'étapes nécessaires pourrait servir à définir une distance ultramétrique sur l'ensemble des treillis équivalents à un treillis donné). L'adverbe "successivement" est important du fait de la redondance relative d'un carré par rapport aux autres.
La simplification d'un treillis redondant est la suppression du maximum de carrés redondants (qui n'est pas, rappelons-le, la suppression de tous les carrés redondants du treillis). On obtient alors un treillis simple. D'après le théorème ci-dessus, les régions et zones rigides d'un treillis ne sont pas modifiées par une simplification du treillis.
Le nombre 
de carrés rigides d'un treillis simplifié est appelé nombre de rigidité du treillis
de départ. 
est nécessairement inférieur ou égal à L + l - 1 et à 
. Un treillis est simple si
et seulement si 
.
Théorème
ne varie pas par passage à un treillis équivalent.
Il est donc bien défini pour un treillis donné.
Démonstration : on peut se réduire aux treillis simples (par définition de 
). Les régions non
dégénérées de taille L et l d'un treillis équivalent étant les mêmes que celles du treillis considéré, et
simples, elles comportent chacune L + l - 1 carrés rigides (longueur et largeur de la zone rigide),
indépendamment du treillis considéré. Puisque de plus les régions dégénérées ne contiennent pas de
carrés rigides, le nombre total de carrés rigides est donc le même que celui du treillis considéré, qui
est bien 
puisque ce treillis est simple.
La différence de 
avec L + l - 1 est égale au nombre de carrés rigides à disposer dans le
treillis initial ou un de ses équivalents pour le rigidifier.
Malheureusement le nombre de rigidité n'est pas caractéristique d'une classe de treillis équivalents.
Théorème
Le nombre de régions d'un treillis t est égal à 
.
On peut se réduire aux treillis simples, pour lesquels 
(en effet, tout treillis est
équivalent à un treillis simple, qui possède le même nombre de rigidité et le même nombre de
régions). L'ajout d'un carré rigide se traduit sur le graphe par la liaison entre deux sommets. Comme
le treillis est simple, le graphe ne comporte pas de boucle, et l'ajout ne peut se faire qu'entre deux
composantes connexes distinctes (sinon en reliant deux sommets d'une même composante connexe,
on crée une boucle). Chaque ajout se traduit donc par la réduction d'une unité du nombre de
composantes connexes (puisqu'on en réunit deux). Au départ, un graphe sans arêtes contient L + l
composantes connexes (les l lignes et L colonnes). Comme on ajoute 
carrés rigides, le graphe
contient finalement 
composantes connexes. CQFD.
Si un treillis quelconque t a pour nombre de rigidité 
, il est toujours possible d'ajouter sans
redondance 
carrés rigides, et t est alors rigide. La démonstration vient encore des
graphes (est-ce vraiment étonnant?). En effet, pour relier n = 
composantes connexes, il
est nécessaire et suffisant d'ajouter n - 1 arêtes au graphe, et cela peut toujours se faire sans créer de
boucle.
Malheureusement, on n'a pas : nombre de carrés redondants + nombre de rigidité = nombre de carrés rigides. En effet, pour avoir cette relation, il faudrait compter un seul carré redondant par boucle du graphe. Et même dans ce cas, évaluer le nombre de boucles dans un graphe complexe serait malaisé : plusieurs boucles peuvent avoir des arêtes communes.
Cependant ce nombre de boucles a un certain rapport avec le nombre de faces dans le cas d'un
graphe planaire. Le nombre n de carrés redondants pouvant être supprimés étant évidemment
, et le nombre de régions 
étant 
, on a évidemment
. Ceci s'interprête en termes de graphes de la manière suivante : 
est le
nombre de sommets 
du graphe, 
le nombre de composantes connexes, 
le nombre
d'arêtes 
. Le nombre de carrés redondants pouvant être supprimés correspond au nombre de
boucles du graphe, qui pour un graphe planaire (pouvant être dessiné dans un plan sans croisement
d'arêtes), est égal au nombre de faces 
. Le résultat précédent donne donc 
, qui est
la classique formule d'Euler pour un graphe planaire. On peut remarquer que ceci permet de
l'étendre à tout graphe biparti, même non planaire (la notion de "face" étant alors celle de "boucle"
du graphe).
Soit E un ensemble fini totalement ordonné. On considère l'ensemble carré E × E : il peut être représenté par un treillis carré de taille card(E), où chaque ligne et chaque colonne représentent un élément de E, de telle manière que la ligne et la colonne de numéro n représentent le n-ième élément de E. On dira qu'un tel treillis représente l'ensemble E.
Soit t un treillis représentant E. On définit la relation R sur E par a R b équivaut à : le carré (a;b) est indéformable. Autrement dit : la ligne b et la colonne a appartiennent à la même région. Deux treillis équivalents représentant E définissent alors la même relation (ils ont les mêmes carrés indéformables).
La relation R possède alors quelques propriétés intéressantes.
En particulier, comme l'indéformabilité des carrés (a;b), (c;b) et (c;d) entraîne celle de (a;d), on aura a R b et c R b et c R d entraîne a R d. On peut même démontrer qu'une relation est représentable par un treillis si et seulement si elle vérifie cette propriété.
De plus, une relation réflexive représentable par un treillis est une relation d'équivalence, dont les classes d'équivalence dans E sont alors les régions du treillis restreintes à leurs lignes (ou colonnes).
Il est possible de généraliser les résultats précédents de diverses manières. La première consiste
à considérer des treillis tels que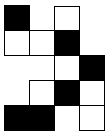 
. Cependant parler de lignes et de colonnes d'un
treillis devient particulièrement risqué. Pour pouvoir parler de directions de lignes et de colonnes
dans le treillis ci-dessus, par exemple, il faut considérer que les carrés (ligne 1;colonne 1) et (ligne
2;colonne 1) d'une part, et (ligne 5;colonne 1) d'autre part, forment deux colonnes distinctes, ou
plutôt deux sous-colonnes, que l'on peut noter colonne 1,1 et 1,2 respectivement. Sous ces
conditions, on peut construire un graphe de la même manière que précédemment. Le théorème
principal devient alors : si le graphe est connexe, le treillis est rigide. L'équivalence est obtenue dans
le cas où le treillis ne comporte pas de "trous". Contre-exemple :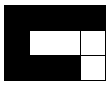 
.
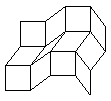
Une autre généralisation possible concerne des treillis en dimension supérieure, par exemple
dans l'espace. Si l'on veut que l'étude soit intéressante, il faut alors considérer des hyperlosanges,
c'est-à-dire qu'on force les arêtes opposées à être parallèles (ce qui en dimension 3 semble
difficilement réalisable). On se permet de plus de rigidifier non pas des hyperlosanges dans leur
ensemble, mais des faces bidimensionnelles de ces losanges. Le théorème central devient alors : le
treillis est rigide si et seulement si tous les "treillis projetés" bidimensionnels sont rigides (je n'ai pas
réussi à prouver ce résultat en n'utilisant que des méthodes de géométrie élémentaire comme
précédemment ; avis aux amateurs). Le nombre de faces à rigidifier pour rigidifier un treillis n-dimensionnel de tailles Li est alors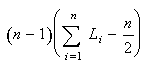 
. Il est toujours possible de tracer des graphes,
en prenant pour sommets des alignements de dimension (n-1) d'hyperlosanges repérés par la donnée
d'une coordonnée. Exemple :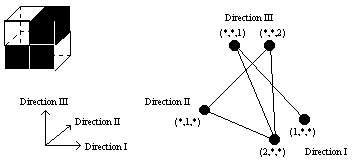 
.