Back to: Main Page > Mathématiques
Séminaire des élèves du département de mathématiques de l'ENS, année 2001
Le séminaire des élèves est généraliste et s'adresse essentiellement aux
élèves de seconde, troisième et quatrième années.
Seuls des élèves en
cours de scolarité ou récemment sortis sont autorisés à y assister...
Participation, renseignements : écrire à yann.ollivier (domain:)
normalesup.org
Les exposés ont lieu le mercredi à 16h30 en salle Cartan.
24 octobre 2001, Julien Marché, L'intégrale de
Kontsevich et ses applications aux algèbres de Lie
Texte (incomplet) : format ps gzippé
Résumé :
On présentera schématiquement l'intégrale construite dans les années 90
par Kontsevich pour décrire de façon combinatoire les invariants de
Vassiliev des noeuds.
Cette intégrale est à valeur dans une algèbre de diagrammes: sa
composition avec une forme linéaire fournit un invariant de type fini. Il
se trouve que chaque algèbre de Lie munie d'une forme bilinéaire donne
lieu à une telle forme linéaire. On retrouve de cette manière tous les
invariants de noeuds (polynôme de Jones, Conway, Kauffman, HOMFLY...).
L'analogie de l'ensemble des diagrammes avec les algèbres de Lie peut
être
poussée un peu plus loin: on construira les analogues des isomorphismes
de Poincaré-Birkhoff-Witt et Duflo pour les algèbres de diagrammes. Les
propriétés de ces isomorphismes sont liées de façon cruciale à la théorie
des noeuds par l'intermédiaire de l'intégrale de Kontsevich.
6 juin : Emmanuel Breuillard, Le paradoxe de
Hausdorff-Banach-Tarski, le problème de Ruziewicz, et l'équidistribution
sur la sphère
Résumé :
Peut-on decouper la sphère en un nombre fini de parties, puis réassembler
ces parties pour former deux copies de la meme sphère ? Paradoxalement
oui, c'est en substance le paradoxe de Hausdorff-Banach-Tarski. Par
conséquent, il n'existe pas de mesure finiment additive et invariante par
rotation définie sur tous les sous-ensembles de la sphère. Qu'en est-il
s'il on se restreint aux sous-ensembles mesurables au sens de Lebesgue ?
La mesure de Lebesgue convient bien sûr, mais est-ce la seule ? C'est le
problème de Ruziewicz.
Une solution définitive à ce problème a été apportée dans les années 80,
tout d'abord, pour le cas des dimensions 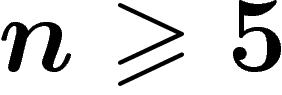 par Margulis et Sullivan,
en construisant un sous-groupe dense dans
par Margulis et Sullivan,
en construisant un sous-groupe dense dans 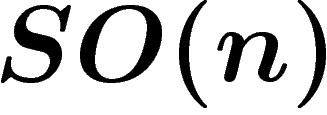 ayant la propriété (T) de
Kazhdan, puis pour
ayant la propriété (T) de
Kazhdan, puis pour 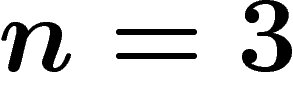 et
et 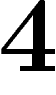 , par Drinfeld, en construisant deux
rotations de la sphère qui engendrent un groupe dense et très bien
équidistribué. Cette dernière construction repose sur la théorie de
Jacquet-Langlands et la conjecture de Ramanujan de la théorie des
nombres. Récemment cependant, Sarnak en a trouvé une preuve plus
élémentaire qui repose sur l'étude d'un certain opérateur de Markov lié
à une marche aléatoire sur la sphère, opérateur qui peut aussi être
interprété comme un opérateur de Hecke pour une classe de formes
modulaires. Le spectre de cet opérateur s'avère avoir des propriétés
statistiques semblables à celui des grandes matrices aléatoires.
, par Drinfeld, en construisant deux
rotations de la sphère qui engendrent un groupe dense et très bien
équidistribué. Cette dernière construction repose sur la théorie de
Jacquet-Langlands et la conjecture de Ramanujan de la théorie des
nombres. Récemment cependant, Sarnak en a trouvé une preuve plus
élémentaire qui repose sur l'étude d'un certain opérateur de Markov lié
à une marche aléatoire sur la sphère, opérateur qui peut aussi être
interprété comme un opérateur de Hecke pour une classe de formes
modulaires. Le spectre de cet opérateur s'avère avoir des propriétés
statistiques semblables à celui des grandes matrices aléatoires.
16 mai : Gilles Radenne, Pavages, surfaces dans un graphe de
Cayley et coloriages
Texte : format ps gzippé
Résumé :
On s'intéresse au problème de la pavabilité d'un figure par un ensemble
de tuiles donné. On va présenter les groupes de pavages introduits par
Conway, et leur utilisation dans la méthode dite des hauteurs, et enfin
on verra comment cette méthode peut se voir sous une approche de
coloriage, ce qui permettra de l'étendre.
On commencera par présenter les groupes de pavages, et quelques une de
leur propriétés élémentaires, puis on va se restreindre à quelques cas
particuliers, dans lesquels on peut donner au graphe de Cayley du groupe
de pavage une conformation dans l'espace qui permettra de définir un
revêtement naturel du 2-simplexe vers le plan de la figure à paver, ce
qui donnera une correspondance entre les pavages signés et des surface
dans le 2-simplexe. On en tirera un algorithme de pavage extrêmement
efficace.
On verra enfin comment cette approche et l'agorithme associé peuvent être
considérés comme un coloriage de la figure à paver, et comment à l'aide
d'un coloriage similaire on peut essayer d'appliquer cette méthode dans
des cas ou le graphe de Cayley n'admet pas de configuration spatiale
utilisable.
9 mai : Grégory Miermont, Introduction à la coalescence
stochastique additive
Texte : dvi ou ps gzippé.
Résumé : On s'intéresse à des processus aléatoires faisant intervenir des
masses 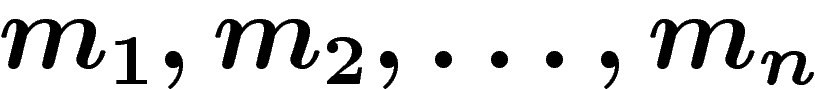 susceptibles de fusionner à des instants
aléatoires dépendant additivement des valeurs des masses. La formation de
gouttes d'eau dans les nuages, ou de galaxies à partir de
"proto-galaxies"
plus petites, constituent des exemples naturels de ce type de processus.
On étudiera des méthodes de codage de ces processus à l'aide d'arbres
aléatoires et de ponts à accroissements échangeables, permettant de
construire les « coalescences éternelles » issues du temps
susceptibles de fusionner à des instants
aléatoires dépendant additivement des valeurs des masses. La formation de
gouttes d'eau dans les nuages, ou de galaxies à partir de
"proto-galaxies"
plus petites, constituent des exemples naturels de ce type de processus.
On étudiera des méthodes de codage de ces processus à l'aide d'arbres
aléatoires et de ponts à accroissements échangeables, permettant de
construire les « coalescences éternelles » issues du temps  avec
des masses « infinitésimales » (microgouttes d'eau dans les nuages,
poussière cosmique dans les galaxies...).
avec
des masses « infinitésimales » (microgouttes d'eau dans les nuages,
poussière cosmique dans les galaxies...).
25 avril : Yann Ollivier, Géométrie des groupes discrets
Texte : html ou pdf ou
ps gzippé.
Résumé : On donnera une introduction à différents thèmes liés à la
géométrie des groupes discrets (un groupe discret est à peu près
n'importe quel groupe sur lequel on met la topologie triviale).
On commencera par donner un aperçu des propriétés usuellement étudiées
(par exemple la propriété de Kazhdan, l'hyperbolicité, la moyennabilité),
avec des exemples, et l'on énoncera quelques-uns des théorèmes-phares de
ce domaine, sans démonstration.
Puis on montrera comment cette approche permet de résoudre partiellement
un problème classique de théorie algorithmique des groupes, à savoir :
trouver un algorithme qui, dans un groupe fini défini par une boîte noire
effectuant la multiplication, renvoie un élément aléatoire uniformément
réparti dans le groupe. La démonstration fait intervenir des propriétés
des groupes discrets infinis, en particulier, de manière cruciale, la
propriété de Kazhdan dont nous aurons préalablement parlé, liée à la
théorie des représentations.
Back to: Main Page > Mathématiques
To leave a comment: contact (domain) yann-ollivier.org
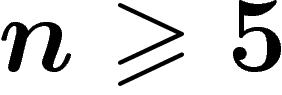 par Margulis et Sullivan,
en construisant un sous-groupe dense dans
par Margulis et Sullivan,
en construisant un sous-groupe dense dans 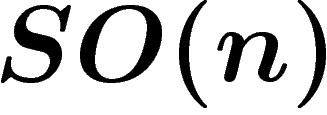 ayant la propriété (T) de
Kazhdan, puis pour
ayant la propriété (T) de
Kazhdan, puis pour 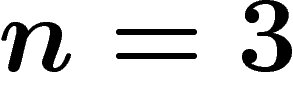 et
et 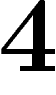 , par Drinfeld, en construisant deux
rotations de la sphère qui engendrent un groupe dense et très bien
équidistribué. Cette dernière construction repose sur la théorie de
Jacquet-Langlands et la conjecture de Ramanujan de la théorie des
nombres. Récemment cependant, Sarnak en a trouvé une preuve plus
élémentaire qui repose sur l'étude d'un certain opérateur de Markov lié
à une marche aléatoire sur la sphère, opérateur qui peut aussi être
interprété comme un opérateur de Hecke pour une classe de formes
modulaires. Le spectre de cet opérateur s'avère avoir des propriétés
statistiques semblables à celui des grandes matrices aléatoires.
, par Drinfeld, en construisant deux
rotations de la sphère qui engendrent un groupe dense et très bien
équidistribué. Cette dernière construction repose sur la théorie de
Jacquet-Langlands et la conjecture de Ramanujan de la théorie des
nombres. Récemment cependant, Sarnak en a trouvé une preuve plus
élémentaire qui repose sur l'étude d'un certain opérateur de Markov lié
à une marche aléatoire sur la sphère, opérateur qui peut aussi être
interprété comme un opérateur de Hecke pour une classe de formes
modulaires. Le spectre de cet opérateur s'avère avoir des propriétés
statistiques semblables à celui des grandes matrices aléatoires.
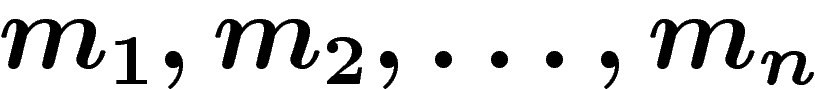 susceptibles de fusionner à des instants
aléatoires dépendant additivement des valeurs des masses. La formation de
gouttes d'eau dans les nuages, ou de galaxies à partir de
"proto-galaxies"
plus petites, constituent des exemples naturels de ce type de processus.
On étudiera des méthodes de codage de ces processus à l'aide d'arbres
aléatoires et de ponts à accroissements échangeables, permettant de
construire les « coalescences éternelles » issues du temps
susceptibles de fusionner à des instants
aléatoires dépendant additivement des valeurs des masses. La formation de
gouttes d'eau dans les nuages, ou de galaxies à partir de
"proto-galaxies"
plus petites, constituent des exemples naturels de ce type de processus.
On étudiera des méthodes de codage de ces processus à l'aide d'arbres
aléatoires et de ponts à accroissements échangeables, permettant de
construire les « coalescences éternelles » issues du temps  avec
des masses « infinitésimales » (microgouttes d'eau dans les nuages,
poussière cosmique dans les galaxies...).
avec
des masses « infinitésimales » (microgouttes d'eau dans les nuages,
poussière cosmique dans les galaxies...).