|
|
Yann OllivierMathematician and computer scientist
Professional Web Page |
 (My employer is not responsible for the contents of this page/Cette page n'engage pas mon employeur.) |
Page
personnelle
The reasonable man adapts himself to the world; the unreasonable man
persists in trying to adapt the world to
himself. Therefore, all progress depends on the unreasonable man.
G. B. Shaw
I am a research scientist at Meta's Fundamental Artificial Intelligence research lab in Paris (formerly at the Centre National de la Recherche Scientifique).
Curriculum
vitæ.
I am currently working on applications of probability theory and information
theory to artificial intelligence and machine learning.
I have also been working in other areas of mathematics including
Markov chains, (discrete) Ricci curvature,
concentration of measure, random groups, hyperbolic
groups, and general
relativity.
You may also visit my personal Web
page. In particular, it contains non-professional, wide-audience
mathematical
texts and mathematical programs.
To reach me: contact (domain:) yann-ollivier.org
Scientific publications by topic
Years in parentheses are the actual time of writing.
For published texts, the year without parentheses is the official
publication year (i.e. the year of actual printing on paper).
Artificial intelligence, learning, optimization
pdf (3562K)
Reinforcement fine-tuning of LLMs is not possible if the initial LLM has zero success rate: then RL methods like GRPO have no learning signal. Here we show the LLM can get unstuck by self-generating "stepping stone" questions. This works via a double RL loop in which a teacher generates questions for a student, the student RL-fine-tunes on those, and the teacher gets rewarded if this improves student performance on the original problems. We show that this works well to kickstart learning on "hard" subsets of standard math benchmarks where the initial success rate is empirically zero after 128 tries.
pdf (3178K)
Training chains of thought (CoT) for LLM reasoning is done via reinforcement learning, generally using 0/1 rewards on validity of the answers. We show that it is equally effective to use the log-probability of a reference answer as the reward. This is more consistent with the log-loss used during pretraining, and makes it possible to do CoT training even when no 0/1 verifier is available.
pdf (2455K)
To appear in ICLR 2026 (final version forthcoming)
pdf (533K)
In a reinforcement learning environment, successor features provide approximate optimal policies for many downstream tasks. We determine algebraically the optimal successor features for three different priors on downstream tasks: goal-reaching, random Gaussian reward functions, and random sparse rewards. Surprisingly, these three priors on downstream tasks lead to the same optimal features: the largest eigenfunctions of the symmetrized inverse Laplacian.
pdf (6858K)
Behavior foundation models (BFM) can tackle any new reward function in a given environment instantly, after an unsupervised pre-training phase. The expressivity of current BFMs is limited by a linear correspondence between the reward and the underlying task representation. Here we break this constraint by introducing auto-regressive features, where finer task representations can depend on a coarser, linear task representation. We also incorporate offline RL techniques into BFM training. Empirically, the offline RL techniques are make-or-break for performance, while autoregressive features only provide moderate gains: this suggests that BFMs are not currently limited by their underlying representation of the environment, but by more mundane RL training considerations.
pdf (4015K)
We conduct a systematic study of the factors affecting the efficiency of learning from fixed offline datasets in RL. We find that neural network size, more than algorithmic considerations, is the key factor influencing performance. We show that simple methods like AWAC and IQL with increased network size notably outperform prior state-of-the-art algorithms on the canonical D4RL benchmark.
pdf (2811K)
We consider imitation learning: the problem of producing a behavior policy that mimics an example trajectory or example trajectories in a given environment. The forward-backward representation of an environment that we introduced in previous work is able to produce a policy from a demonstrated trajectory within seconds via simple calculations, while traditional approaches need to perform lengthy learning on each new task or trajectory.
pdf (1262K)
We test methods for zero-shot reinforcement learning: an agent must first learn a representation of an environment from reward-free interactions, then be able to optimize any task in that environment with no additional planning or learning. We test many models based on successor features (SFs) and on the forward-backward (FB) representations we recently introduced. On tasks from the Unsupervised RL benchmark, FB representations work best, reaching about 85% performance of an algorithm with access to rewards. SFs only work well when based on Laplacian eigenfunctions.
pdf (1514K)
We establish that a physical system can perform statistical learning without gradient computations, by combining energy minimization, homeostatic control, and nudging towards the correct response. The specifics of the system do not have to be known: the procedure is based only on external manipulations, and produces a stochastic gradient descent without explicit gradient computations. This considerably widens the range of potential hardware for statistical learning to any system with enough controllable parameters, even if the details of the system are poorly known. This also establishes that in natural (bio)physical systems, genuine gradient-based statistical learning may result from generic, relatively simple mechanisms.
pdf (1475K)
We prove the existence of a representation of the dynamics of a Markov decision process, on which one can directly read all optimal policies for all possible reward functions in the environment. This "forward-backward" representation is learnable from reward-free interaction, via standard deep learning techniques. Experimentally, this provide instantaneous adaptation to position-dependent tasks in the MsPacman game or a simple virtual robotic arm. This is a step towards learning fully controllable agents in arbitrary black-box environments.
pdf (1311K)
In reinforcement learning, successor states represent all possible paths in an environment together with their probability. We show how to learn this object, which can be used for goal-dependent reinforcement learning or for computing the value functions of all reward functions. Notably, such learning can start even before any reward is observed. The resulting algorithms encode path compositionality in the environment; in particular, the Bellman-Newton algorithm corresponds to path concatenation.
pdf (2992K)
In multi-goal reinforcement learning, the reward for each goal is sparse, located in a small neighborhood of the goal. In large dimension, the probability of reaching a reward vanishes and the agent receives little learning signal. Multi-goal RL methods such as Hindsight Experience Replay tackle this at the price of being biased. First, we prove that HER is actually unbiased in deterministic environments. For stochastic environments, we tackle sparse rewards by directly taking the infinitely sparse, Dirac reward limit, which can be handled algebraically in Q-learning methods.
pdf (1052K)
We prove local convergence of several algorithms used in machine learning, including adaptive algorithms (RMSProp, Adam, online natural gradient...) and recurrent algorithms (RTRL, truncated backprop through time, NoBackTrack, UORO...). This results from a dynamical system viewpoint that emphasizes several differences with standard SGD theory; notably, cycling or sampling without replacement over a finite dataset acts as a variance reduction method that theoretically allows for larger learning rates than pure SGD.
pdf (673K)
We identify which machine learning regularization terms have an interpretation as the influence of a prior in the Bayesian variational inference approach. This also provides a prediction for useful values of the regularization factor in neural networks for various common penalties.
pdf (2515K)
Standard Q-learning algorithms for reinforcement learning are not robust to changes of time discretization, such as changing the framerate or the frequency of sensors and actuators. When time discretization tends to 0, these algorithms collapse, both empirically and theoretically. The reason is that the Q-learning equations are not physically homogeneous and do not admit a continuous-time limit (the Q function collapses to the value function). We analyze this phenomenon and propose and test well-founded solutions, leading to increased robustness.
pdf (10253K)
In reinforcement learning, the decay factor controls the timescale over which the consequences of actions are taken into account. Larger decay factors are more precise but slower to learn. We show that the value function decomposes naturally as a sum of value functions at different timescales, each of which can be learned based on the smaller timescales, in a hierarchical manner. This makes it possible to learn short-term effects fast, while still accounting for long-term effects.
pdf (1655K)
Membership inference determines, given a sample and a trained machine learning model, whether the sample was part of the training set. We derive a theoretically optimal strategy in a Bayesian framework, and relate it to several existing and new practical heuristics, also improving performance on ImageNet.
pdf (675K)
The extended Kalman filter is the standard tool to estimate in real time the current state of a dynamical system based on noisy measurements of a part of the system, used for instance in GPS navigation. For nonlinear systems some aspects of this filter could be considered arbitrary, but we recover it from first principles of statistical learning: this filter is a natural gradient descent on the log-likelihood of the observations, where the whole hidden trajectory of the system is seen as the parameter to be estimated.
pdf (3124K)
In neural networks, the learning rate of the gradient descent is a crucial hyperparameter, whose tuning is time-consuming and prevents out-of-the-box training of a model. We propose the All Learning Rates At Once (Alrao) algorithm: each unit or feature in the network gets its own learning rate sampled from a random distribution spanning several orders of magnitude, in the hope that enough units will get a close-to-optimal learning rate. Perhaps surprisingly, stochastic gradient descent (SGD) with Alrao performs close to SGD with an optimally tuned learning rate, for various network architectures and problems.
pdf (398K)
Temporal difference (TD) is the most basic algorithm in reinforcement learning. For large problems, the value function over states has to be approximated by a parametric family, and approximate TD is known to exhibit divergence except for linear approximations. We prove that if the policy of the agent is reversible (an assumption which implies that every move can be undone), approximate TD is a gradient descent of the so-called "Dirichlet norm" of the error on the value function, and will thus converge to a locally best approximation in this norm.
pdf (362K)
Deep learning models often have more parameters than observations. We show experimentally that in spite of this, deep neural networks can compress the data losslessly even when taking the cost of encoding the parameters into account. Surprisingly, a traditional method designed for this, variational inference, performs very poorly compared to "prequential" methods imported from the Minimum Description Length toolbox. This corroborates the hypothesis that good compression on the training set correlates with good test performance.
pdf (487K)
Adversarial examples for neural networks are tiny perturbations of the inputs that fool the network and have a huge effect on its prediction. Thsi is directly linked to the size of gradients of the network wrt its inputs. We show that the norm of these gradients grows like the square root of the input dimension for many network architectures. In particular, the problem worsens with high-res images. We prove that adversarial training is equivalent to adding a dual norm gradient penalty in the loss function.
pdf (4369K)
Generative adversarial networks (GANs) provide feedback to a generative network via a discriminator network. However, the discriminator usually assesses individual samples. This prevents the discriminator from accessing global distributional statistics of generated samples, and often leads to mode dropping: the generator models only part of the target distribution. We propose to feed the discriminator with mixed batches of true and fake samples, and train it to predict the ratio of true samples in the batch. This is based on a provably universal architecture for computing permutation-invariant statistics. Experimentally, our approach reduces mode collapse in several datasets.
pdf (528K)
We introduce a simple algorithm that converges to a true natural gradient descent in the limit of small learning rates, without explicit Fisher matrix estimation. In large dimension, small learning rates will be required to approximate the natural gradient well. Still, this shows it is possible to get arbitrarily close to exact natural gradient descent with a lightweight algorithm.
pdf (973K)
We justify from first principles a key part of LSTMs, a popular neural network structure for modelling sequential data and time series. This structure follows from a simple axiom of resilience to time warpings, i.e., arbitrary time deformations in the inputs or desired outputs of the model, such as variable accelerations or decelerations. This also suggests a new initialization that empirically captures long-term dependencies better.
pdf (357K)
Proc. of the conference on Geometric Science of Information (GSI 2017), F. Nielsen and F. Barbaresco (eds), Lecture Notes in Computer Science 10589, Springer (2017), 451–459. (Best paper award.)
One way to avoid overfitting in machine learning is to add a controlled amount of noise to stochastic gradient descents, that ensures convergence to the Bayesian posterior on model parameters. The theoretically optimal covariance of the noise is the inverse Fisher metric. We show how to implement this in practice with neural networks using efficient Fisher metric approximations. On MNIST, this performs similarly to dropout as a regularization method.
pdf (423K)
Truncated backpropagation through time is the standard algorithm for online learning of recurrent neural networks and other dynamical systems. It backpropagates gradients only a fixed amount of steps in the past along the training sequence, to reduce computational cost, and is equivalent to chopping the sequence into shorter subsequences and training independently. This introduces biases. We introduce a trick that removes this bias by randomizing the truncation lengths and introducing compensation factors in the backprop equation.
pdf (550K)
We prove an exact algebraic equivalence between two algorithms for parameter training, namely, Amari's natural gradient applied online, and the extended Kalman filter used to estimate the parameter (assumed to have constant dynamics). This also applies to recurrent (non-iid, state space model) systems. This correspondence provides relevant settings for natural gradient hyperparameters such as Fisher matrix initialization and smoothing.
pdf (492K)
Recurrent neural networks are usually trained via the backpropagation through time algorithm, which is not online as it requires access to the full training sequence. We introduce UORO: like our previous NoBacktrack algorithm, it provides a noisy but unbiased estimate of the gradient of the system, online at small computational cost. But unlike NoBacktrack, it bypasses the need for model sparsity and can be implemented in a black-box fashion on top of any given model. It can largely beat truncated backprop through time for instance when a parameter has a positive short-term influence but a negative long-term one.
Torch code available at https://github.com/ctallec/uoro
Please disregard some figures in the first ArXiv version of this text (corrected in the current versions): UORO and TruncatedBP were not displayed in exactly the same way; losses for BP truncated to 16 were displayed smoothed over a 16 times longer range, which falsely gave the impression that UORO was much noisier.
pdf (606K)
We provide the first experimental results on non-synthetic datasets for the quasi-diagonal Riemannian gradient descents for neural networks introduced in Riemannian metrics for neural networks I: Feedforward networks. These methods reach a good performance faster than simple stochastic gradient descent, thus requiring shorter training. We also present an implementation guide to these Riemannian methods so that they can be easily implemented on top of existing neural network routines to compute gradients.
Torch class for the simplest algorithm presented (QDOP gradient). (Use: just replace the usual nn.Linear modules with nnx.QDRiemaNNLinear2 modules and readjust the learning rates.)
pdf (856K)
Recurrent neural networks are usually trained via the backpropagation through time algorithm, which is not online as it requires access to the full training sequence. Known online algorithms such as real-time recurrent learning or Kalman filtering have large computational and memory requirements. We introduce the NoBackTrack algorithm, which maintains, at each step, a search direction in parameter space. This search direction evolves in a way built to provide, at every time, an unbiased estimate of the exact gradient direction. This can be fed to a Kalman-like filter. For RNNs these algorithms scale linearly with the number of parameters.
Presentation slides
Code (tar.gz) used in the experiments
pdf (1955K)
The practical performance of online stochastic gradient descent algorithms is highly dependent on the chosen step size, which must be tediously hand-tuned in many applications. We propose to adapt the step size by performing a gradient descent on the step size itself, viewing the whole performance of the learning trajectory as a function of step size. Importantly, this adaptation can be computed online at little cost, without having to iterate backward passes over the full data.
pdf (418K)
Proc. of the conference on Geometric Science of Information (GSI 2015), F. Nielsen and F. Barbaresco (eds), Lecture Notes in Computer Science 9389, Springer (2015), 311–319.
Laplace's "add-one" rule of succession modifies the observed frequencies in a sequence of heads and tails by adding one to the observed counts. This improves prediction by avoiding zero probabilities and corresponds to a uniform Bayesian prior on the parameter. We prove that, for any exponential family of distributions, arbitrary Bayesian predictors can be approximated by taking the average of the maximum likelihood predictor and the sequential normalized maximum likelihood predictor from information theory, which generalizes Laplace's rule. Thus it is possible to approximate Bayesian predictors without the cost of integrating or sampling in parameter space.
Presentation slides (GSI 2015).
php
Notes edited by Jérémy Bensadon.
Notes of a series of 2014 talks on aspects of information theory applied to the theory of induction and statistical learning. Kolmogorov complexity, universal induction and prediction, minimum description length, model selection, Fisher information and confidence intervals, Bayesian priors, gradient methods, expectation-maximization and natural gradients, regularization, variational approaches...
pdf (590K)
Auto-encoders aim at building a more compact representation of a dataset, by constructing maps 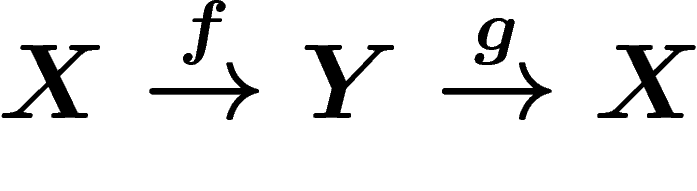 from data space to a smaller "feature space" and back, with small reconstruction error. We discuss the similarities and differences between training an auto-encoder to minimize the reconstruction error, and training the same auto-encoder to actually compress the data. In particular we provide a connection with denoising auto-encoders, and prove that the compression viewpoint determines an optimal data-dependent noise level.
from data space to a smaller "feature space" and back, with small reconstruction error. We discuss the similarities and differences between training an auto-encoder to minimize the reconstruction error, and training the same auto-encoder to actually compress the data. In particular we provide a connection with denoising auto-encoders, and prove that the compression viewpoint determines an optimal data-dependent noise level.
pdf (1134K)
Recurrent neural networks, a powerful probabilistic model for sequential data, are notoriously hard to train. We propose a training method based on a metric gradient ascent inspired by Riemannian geometry. The metric is built to achieve invariance wrt changes in parametrization, at a low algorithmic cost. This is used together with gated leaky neural networks (GLNNs), a variation on the model architecture. On synthetic data this model is able to learn difficult structures, such as block nesting or long-term dependencies, from only few training examples.
Code (tar.gz) used for the experiments.
pdf (828K)
We describe four algorithms for neural network training, each adapted to different scalability constraints. These algorithms are mathematically principled and invariant under a number of transformations in data and network representation, from which performance is thus independent. These algorithms are obtained from the setting of differential geometry, and are based on either the natural gradient using the Fisher information matrix, or on Hessian methods, scaled down in a specific way to allow for scalability while keeping some of their key mathematical properties.
pdf (5169K)
When using deep, multi-layered architectures to build generative models of data, it is difficult to train all layers at once. We propose a layer-wise training procedure admitting a performance guarantee compared to the global optimum. We interpret auto-encoders as generative models in this setting. Both theory and experiments highlight the importance, for deep architectures, of using an inference model (from data to hidden variables) richer than the generative model (from hidden variables to data).
pdf (311K)
FOGA (Foundations of Genetic Algorithms) XII, 2013.
Guarantees of improvement over the course of optimization algorithms often need to assume infinitesimal step sizes. We prove that for a class of optimization algorithms coming from information geometry, IGO algorithms, such improvement occurs even with non-infinitesimal steps, with a maximal step size independent of the function to be optimized.
pdf (918K)
Journal of Machine Learning Research 18 (2017), n°18, 1–65.
The information-geometric optimization (IGO) method is a canonical way to turn any smooth parametric family of probability distributions on an arbitrary, discrete or continuous search space X into a continuous-time black-box optimization method on X. It is defined thanks to the Fisher metric from information geometry, to achieve maximal invariance properties under various reparametrizations. When applied to specific families of distributions, it naturally recovers some known algorithms (such as CMA-ES from Gaussians). Theoretical considerations suggest that IGO achives minimal diversity loss through optimization. First experiments using restricted Boltzmann machines show that IGO may be able to spontaneously perform multimodal optimization.
pdf (242K)
ps.gz
Proc. AAAI-07, Vancouver, Canada, July 2007, 1427–1433.
The goal is to find "related nodes" to a given node in a graph/Markov chain (e.g. a graph of Web pages). We propose the use of discrete Green functions, a standard tool from Markov chains. We test this method versus more classical ones on the graph of Wikipedia. Accompanying Web site.
pdf (211K)
ps.gz
Random Struct. Algor. 23 (2003), n° 1, 58–72.
We study the genetical dynamics of mating (crossover) operators in finite populations. We prove that the convergence to equilibrium is exponential but that there is a non-eventually vanishing bias depending on population size.
Ricci curvature, Markov chains, concentration
pdf (333K)
In Analysis and Geometry of Metric Measure Spaces: Lecture Notes of the 50th Séminaire de Mathématiques Supérieures (SMS), Montréal, 2011, Galia Dafni, Robert McCann, Alina Stancu, eds, AMS (2013).
We try to provide a visual introduction to some objects from Riemannian geometry: parallel transport, sectional curvature, Ricci curvature, Bianchi identities... We also present some of the existing generalizations of these notions to non-smooth or discrete spaces, insisting on Ricci curvature.
pdf (258K)
SIAM J. Discr. Math. 26 (2012), n°3, 983–996.
We compare two approaches to Ricci curvature on non-smooth spaces, in the case of the discrete hypercube 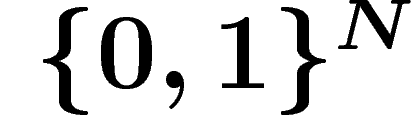 . Along the way we get new results of a combinatorial and probabilistic nature, including a curved Brunn–Minkowski inequality on the discrete hypercube.
. Along the way we get new results of a combinatorial and probabilistic nature, including a curved Brunn–Minkowski inequality on the discrete hypercube.
pdf (550K)
ps.gz (470K)
Ann. Probab. 38 (2010), n°6, 2418–2442.
Under a discrete positive curvature assumption, we get explicit finite-time bounds for convergence of empirical means in the Markov chain Monte Carlo method. This allows to improve known bounds on several examples such as the Ornstein-Uhlenbeck process, waiting queues, spin systems at high temperature or Brownian motion on positively curved manifolds.
pdf (379K)
ps.gz (230K)
in Probabilistic approach to geometry, Adv. Stud. Pure Math. 57, Math. Soc. Japan (2010), 343–381.
This is a gentle introduction to the context and results of my article Ricci curvature of Markov chains on metric spaces. It begins with a description of classical Ricci curvature in Riemannian geometry, as well as a reminder for discrete Markov chains. A number of open problems are mentioned.
pdf (560K)
ps.gz (291K)
J. Funct. Anal. 256 (2009), n°3, 810–864.
Some of the results are announced in the note
Ricci curvature of metric spaces, C.R. Math. Acad. Sci Paris 345 (2007), n°11, 643–646.
(Erratum: In theorem 49 (and only there), we need to assume that X is locally compact. This is omitted in the published version.)
Additional details for the proof of Proposition 6.
php
Notes (in French) of a working seminar I organized in 2004 about the various approaches to concentration of measure (geometrical, analytical, probabilistic).
pdf (268K)
ps.gz
Master's dissertation, advised by P. Pansu.
I explain some of the results of Gromov's "Chapter 3 1/2", about the observable diameter and concentration of measure on submanifolds of the sphere and on some projective complex algebraic varieties.
Random groups, geometric group theory
pdf (1658K)
ps.gz (1130K)
Ensaios Matemáticos [Mathematical Surveys], 10. Sociedade Brasileira de Matemática, Rio de Janeiro, 2005.
Small book reviewing currently known facts and numerous open problems about random groups. This text is aimed at those having some basic knowledge of geometric group theory and wanting to discover the precise meaning of "random groups" and hopefully provides a roadmap to working on the subject.
January 2010 random groups updates
How to order a printed copy.
pdf (227K)
ps.gz (250K)
Trans. Amer. Math. Soc. 359 (2007), n°5, 1959–1976.
We prove that any countable group embeds in 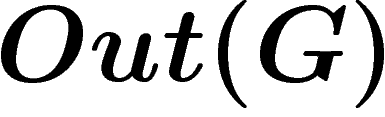 for some group G with property
for some group G with property 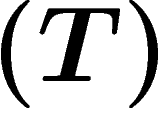 (this answers a question of Paulin). We also get Kazhdan groups which are not Hopfian, or not coHopfian. For this we use the graphical small cancellation technique of Gromov.
(this answers a question of Paulin). We also get Kazhdan groups which are not Hopfian, or not coHopfian. For this we use the graphical small cancellation technique of Gromov.
pdf
ps.gz
C.R. Math. Acad. Sci. Paris 341 (2005), n°3, 137–140.
Random quotients of hyperbolic groups with "harmful" torsion collapse at densities smaller than expected.
pdf
ps.gz
Expository manuscript.
Simple proof that property 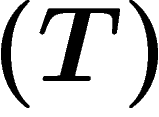 is equivalent to a uniform spectral gap for the random walk operator with values in unitary representations, and of the
is equivalent to a uniform spectral gap for the random walk operator with values in unitary representations, and of the 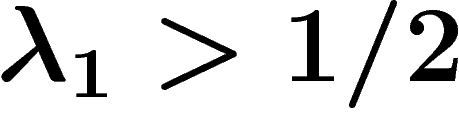 criterion.
criterion.
pdf
ps.gz
Expository manuscript.
Description of the steps in Gromov's construction of a group whose Cayley graph contains (more or less isometrically) a family of expanders, with some technical points.
pdf (280K)
ps.gz
Comment. Math. Helv. 81 (2006), n° 3, 569–593.
The growth exponent of a generic group (in the density model) is arbitrarily close to that of the free group. This answers a question of Grigorchuk and de la Harpe.
pdf (309K)
ps.gz
Ann. Inst. Fourier (Grenoble) 55 (2005), n° 1, 289–317.
We show that the spectral gap of the Laplacian (or random walk operator) on a generic group is very probably almost as large as in a free group. Moreover this spectral gap is robust under random quotients of hyperbolic groups (in the density model).
pdf (377K)
Bull. Belg. Math. Soc. 13 (2006), n° 1, 75–89.
If a group presentation has for relators the words read on the cycles of a labelled graph, and if the labelling satisfies a generalized small cancellation condition, then the group is hyperbolic. Note: this version rectifies a mistake in the proof of the isometric embedding property in the published version.
pdf (838K)
GAFA, Geom. Funct. Anal. 14 (2004), n° 3, 595–679.
Generalisation of Gromov's result that a random group is infinite hyperbolic if the number of relators is less than some critical value and trivial above this value: this is still true when taking a random quotient of a hyperbolic group. The critical value can be computed and depends on the properties of the random walk on the group.
2003 (2002)
Critical densities for random quotients of hyperbolic groups
C.R. Math. Acad. Sci. Paris 336 (2003), n° 5, 391–394.
Short paper announcing the results of Sharp phase transition theorems for hyperbolicity of random groups.
General relativity and statistical physics
(2008)
On the kinetic Fokker–Planck equation in Riemannian geometry
pdf (327K)
Nonlinear Analysis: Theory, Methods & Applications 71 (2009), n°12, e199–e202.
This is a survey of our results on the large-scale effects of fluctuations in cosmology. It contains a synthesis of results from the texts below.
pdf
ps.gz
Physica A 388 (2009), 5029–5035.
Since general relativity is non-linear, fluctuations (e.g. gravitational waves or irregularities in matter density) around a given mean produce non-zero average effects. For example, we show that gravitational waves of currently undetectable amplitude and frequency could influence expansion of the universe roughly as much as the total matter content of the universe. This should be taken into account when considering dark matter/dark energy problems.
pdf
ps.gz
Astron. Astrophys. 433 (2005), n°2, 397–404.
Observing a fluctuating black hole yields the impression that it is surrounded with ``apparent matter'' of negative energy.
Miscellaneous
pdf (515K)
The introduction (in French) of my Habilitation manuscript, which contains a presentation of my research for a general mathematical audience.
pdf (1210K)
ps.gz (574K)
Advisors: M. Gromov and P. Pansu
My PhD dissertation. In addition to an overall presentation, it mainly contains some of the texts above.
pdf (286K)
For diffusion processes, we sum up the relationship between drift, diffusion matrix, and invariant distributions, using the "right" variables. This yields a decomposition into a potential and geometric parts of the drift. Physical Langevin processes on the pair (position, speed) with noise on speed, come up naturally.
Various texts on my personal Web page, eg: the various meanings of entropy in mathematics; introduction to concentration of measure; presentation of different cohomology theories in various settings; introductions to geometric group theory; and more. (Mostly in French.)
To reach me: contact (domain:) yann-ollivier.org
Last modified: February 5, 2026.



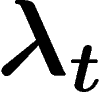 in Eq.19, please refer to this version.)
in Eq.19, please refer to this version.) from data space to a smaller "feature space" and back, with small reconstruction error. We discuss the similarities and differences between training an auto-encoder to minimize the reconstruction error, and training the same auto-encoder to actually compress the data. In particular we provide a connection with denoising auto-encoders, and prove that the compression viewpoint determines an optimal data-dependent noise level.
from data space to a smaller "feature space" and back, with small reconstruction error. We discuss the similarities and differences between training an auto-encoder to minimize the reconstruction error, and training the same auto-encoder to actually compress the data. In particular we provide a connection with denoising auto-encoders, and prove that the compression viewpoint determines an optimal data-dependent noise level.
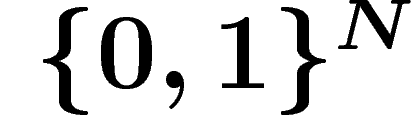 . Along the way we get new results of a combinatorial and probabilistic nature, including a curved Brunn–Minkowski inequality on the discrete hypercube.
. Along the way we get new results of a combinatorial and probabilistic nature, including a curved Brunn–Minkowski inequality on the discrete hypercube.
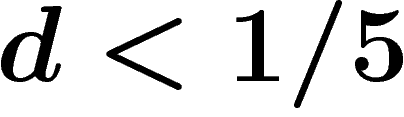 have a codimension-1 subgroup and thus do not have property
have a codimension-1 subgroup and thus do not have property 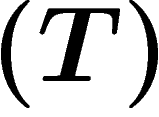 . Moreover at density
. Moreover at density 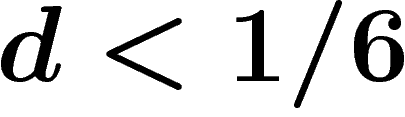 they act freely and cocompactly on a CAT(0) cube complex and thus have the Haagerup property.
they act freely and cocompactly on a CAT(0) cube complex and thus have the Haagerup property.
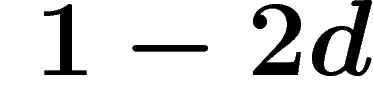 . Also when
. Also when 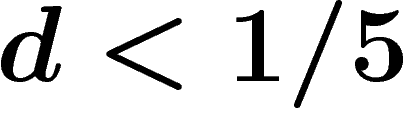 the random presentation satisfies the Dehn algorithm, whereas it does not for
the random presentation satisfies the Dehn algorithm, whereas it does not for 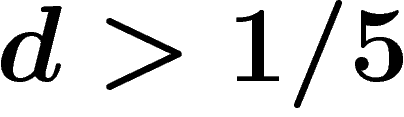 . We use a somewhat improved local-global criterion.
. We use a somewhat improved local-global criterion.
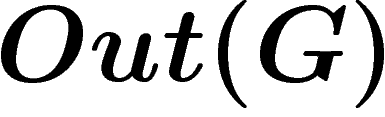 for some group G with property
for some group G with property 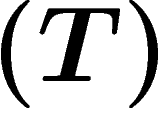 (this answers a question of Paulin). We also get Kazhdan groups which are not Hopfian, or not coHopfian. For this we use the graphical small cancellation technique of Gromov.
(this answers a question of Paulin). We also get Kazhdan groups which are not Hopfian, or not coHopfian. For this we use the graphical small cancellation technique of Gromov.
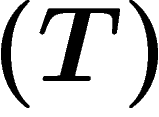 is equivalent to a uniform spectral gap for the random walk operator with values in unitary representations, and of the
is equivalent to a uniform spectral gap for the random walk operator with values in unitary representations, and of the  criterion.
criterion.